Introduction

• As we know that computer system stores any data in binary form thats why we use to add the word DIGITAL with all the work related to computer.
• The data stored in computer is knows as Digital Data.
• In this chapter we will see various techeniques to represent data in a computer system.
• Human beings have adopted Decimal Number System in their day to day life. In the same manner, computer system has adopted Binary Number System, Octal Number System and Hexadecimal Number System which are combinely known as Digital Number System.
• These Number Systems are –

Decimal number system

• Decimal system is consists of 10 digits which are as under
• 0,1,2,3,4,5,6,7,8,9
• Base of this system is 10 and it is to be shown as-
• (1249)₁₀
• This techenique is based on positional value where the weightage of a digit is as per its position. For ex- in number 526, the value of 5 is 500, value of 2 is 20 and value of 6 is 6. (it is as per the method of hundreds , tens and ones).
• We can write above given example as-
• 526 = 5 X 10² + 2 X 10¹ + 6 X 10⁰
• 25.32 = 2 X 10¹ + 5 X 10⁰ + 3 X 10^-1 + 2 X 10^-2
• The left most digit is called MSD (Most Significant Digit ).
• The right most digit is called LSD (Least Significant Digit ).

Binary Number System

• Binary system consists of 2 digits 0,1 known as bit.
• Base of this system is 2 and it is to be shown as (1001010101)₂
• In Digital systems, use of decimal system is immpossible therefore use of binary system for a computer system is meaningful. Use of circuit to maintain two voltage level is very easy.
• See the examples of binary number method-
• 1010 = 1 X 2³ + 0 X 2² + 1 X 2¹ + 0 X 2⁰
• 10.11 = 1 X 2¹ + 0 X 2⁰ + 1 X 2^-1 + 1 X 2^-2
• The left most digit is called MSB (Most Significant Bit ).
• The right most digit is called LSB (Least Significant Bit ).

Octal Number System

• Octal system consists of 8 digits which are as under-
  0,1,2,3,4,5,6,7
• Base of this system is 8 and it is to be shown as
  (1675)₈
• Example to show Octal Number method-
• 147 = 1 X 8² + 4 X 8¹ + 7 X 8⁰
• 13.46 = 1 X 8¹ + 3 X 8⁰ + 4 X 8^-1 + 6 X 8^-2

Hexadecimal Number System

• Hexadecimal system consists of 16 digits which are-
  0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F
• Here A=10, B=11, C=12, D=13, E=14, F=15
• Base of this system is 16 and it is to be shown as
  (16A7B5)₁₆
• Example of Hexadecimal Number method –
• 1A7 = 1 X 16² + 10 X 16¹ + 7 X 16⁰
• 1B.A6 = 1 X 16¹ + 11 X 16⁰ + 10 X 16^-1 + 6 X 16^-2

Relation between different Number Systems

Number Conversion
• Follow the following diagram to convert a number from one system to another.

Decimal to Binary

• For this, decimal value is to be divided by 2 and remainder is to be arrange in order. Quotient is again to be divide by 2 and remainder is to be again kept in order. This process is to be repeated until quotient become zero. Remainder is then to keep in reverse order which results in binary of the given number .(remainder should be either 0 or 1 only).

Decimal to Binary
You need to develop a table of 2ⁿ

Decimal to Binary

• If decimal value is with fractional part, the method for the integer part will be same as before. Fractional part is to be multiplied by 2 and the digit before (.) is to be wriiten with binary after applying (.). This process is to be repeated until we get the desired result.
• For example- to convert (259.25)₁₀ in to Binary-

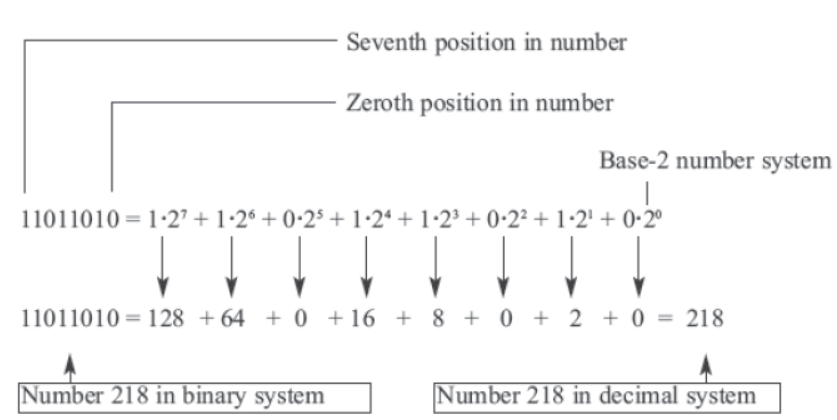
Binary to Decimal

• For this, every bit of binary is multiplied by 2 after applying power as per its position.
• The resultant expression is then to be solved mathematically.
• For ex- to convert (11011010)₂ into decimal

Binary to Decimal

• To solve binary with fractional part, consider the followng example

Decimal to Octal

• For this, decimal value is to be divided by 8 and remainder is to be arrange in order. Quotient is again to be divide by 8 and remainder is to be again kept in order. This process is to be repeated until quotient become zero. Remainder is then to keep in reverse order which results in octal of the given number. (remainder should come in between 0 to 7 only.)
• For ex- to convert (239)₁₀ into Octal-

Octal to Decimal

• For this, every digit of octal is multiplied by 8 after applying power as per its position.
• The resultant expression is then to be solved mathematically.
• For ex- to convert 345 octal to decimal –

345 octal = (3 * 82) + (4 * 81) + (5 * 80)
= (3 * 64) + (4 * 8) + (5 * 1)
= 229 decimal

• Another example –
  24.6₈ = 2 X 8¹ + 4 X 8⁰ + 6 X 8^-1 = 20.75₁₀

Decimal to Hexadecimal

• For this, decimal value is to be divided by 16 and remainder is to be arrange in order. Quotient is again to be divide by 16 and remainder is to be again kept in order. This process is to be repeated until quotient become zero. Remainder is then to keep in reverse order which results in hexadecimal of the given number. (remainder should come in between 0 to 15 only). A is to be written for 10, B for 11………. F for 15.

Hex to Decimal

• For this, every digit of Hex is multiplied by 16 after applying power as per its position.
• The resultant expression is then to be solved mathematically.
• For ex-
  356₁₆ =3 X 16² + 5 X 16¹ + 6 X 16⁰ = 768 + 80 + 6 = 854₁₀
  2AF₁₆ = 2 X16² + 10 X 16¹ + 15 X 16⁰
  = 512 + 160 + 15
  = 687₁₀
• Another example-
  56.08₁₆ = 5 X16¹ + 6 X 16⁰ + 0 X 16^-1 + 8 X 16^-2
  = 80 + 6 + 0 + 8/256
  = 86 + 0.03125
  = 86.03125

Octal ⟷ binary

• For this, first convert the octal to decimal and then the received decimal to binary.
• Another method is with the help of Octal Table-

(235)₈ = (010_^¯011101)₂
Every digit of octal is to be replaced by its relevant binary value.
(¯101110¯100)₂= (564)₈
First, combine three-three digits from right and then write their concerned octal value from table.

Hex ⟷ binary

• For this, first convert the hex to decimal and then the received decimal to binary.
• Another method is with the help of Hex Table-

(2A5)₁₆ = (001010100101)₂
Just write binary of each hex digit at its place.
(000101110100)₂= (174)₁₆
First, combine four-four digits from right and then write their concerned hex value from table.

Octal ⟷ Hex

• For this, you can write binary from octal table and then convert it to hex. Reverse the process to convert from hex to octal.
• Another method with table-

Binary – Unsigned Integers

• An unsigned integer can be any positive value or 0 (Zero).
• Any negative (-ve) value can’t be unsigned integer.
• Unsigned Integer can be from 0 से 2n – 1.

Binary Addition

• Consider following during Binary Addition-
  0 + 0 = 0
  0 + 1 = 1
  1 + 0 = 1
  1 + 1 = 11 , important point to notice here is that 1 goes for carry which is to be added with next place bit.

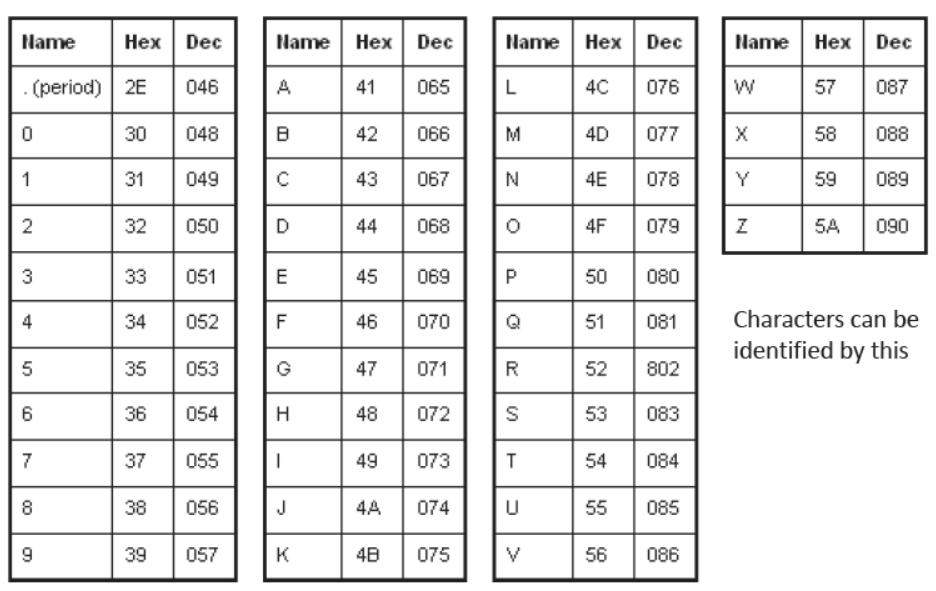
ASCII Code

• The ability of a computer system to understand signals or letters depends on its character set.
• Character set has its standards known as character set code like
• ASCII, ISCII, UNICODE etc.
• ASCII ( American Standard Code for Information Interchange) most of the micro computers, mini computers and some mainframe computers uses this code.
• ASCII code has two versions – ASCII – 7 and ASCII – 8.
• ASCII – 7 code use 7 bits for one signal or character. By this, 2⁷
  = 128 , different characters can be used.
  ASCII – 8 code use 8 bits for one signal or character. By this, 2⁸
  = 256 , different characters can be used.

ASCII Code

ISCII Code

• Indian Standard Code for Information Interchange is developed in India.
• It identifies signals and charaters of almost all indian languages
• It identifies ASCII script along with subscripts of various indian languages.
• It also works in the 8 bit group.

Unicode

• This is Universal Character Set which represents a signal or a character in a group of 32 bit.
• It has the capability to include signals and characters from all scripts of all languages of world.
• Before the development of Unicode, various encoding system were in use.
• Problems related to language on internet has been resolved by the use of Unicode.