Sample Paper Class 12 Mathematics
Get Class 12 Mathematics Sample Papers free pdf download which is based on the latest pattern of CBSE and NCERT. It involves every one of the points given in NCERT class 12 Mathematics book. You can easily download sample paper accounts class 12 is given below.
Download 12th Mathematics Question paper in PDF free of charge. It will help you to make your preparation better to score higher marks in exams. These Class 12 Mathematics Sample Papers PDFs are prepared by our expert teacher.
This 12th Mathematics Question Paper PDF assists you with revising the complete chapter in minutes. One of the best tips suggested by teachers is Solving the sample papers during exam time.
We bring here the latest collection of Sample Papers for Class 12 Mathematics prepared as per the latest examination pattern issued by CBSE. Students can refer to the latest paper below available with answers and also download the suggested guess papers in PDF format for free. Students should solve the papers in exam type environment at home and then compare their results with the answers provided below. Students should regularly solve questions given in DK Goel Class 12 book and also solve the papers given below
Sample Paper Class 12 Mathematics Term 2 Set A
Section – A
1. Evaluate : ∫3x2/x6+1dx
OR
Find the value of integral :∫tan3x/cos3xdx.
Answer:

2. If q is the angle between two vectors î- 2ĵ+3k̂ and 3 î-2 ĵ+k̂
find sin θ
Answer:
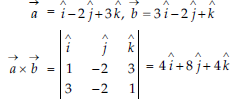
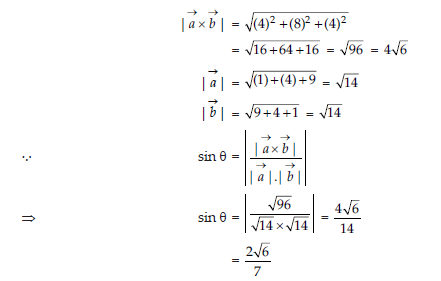
3. Solve the following differential equation :
dy/dx= x3 cosec y, given that y(0) = 0
Answer:

4. A black and a red die are rolled together. Find the conditional probability of obtaining the sum 8, given that the red die resulted in the number less than 4.
Answer:
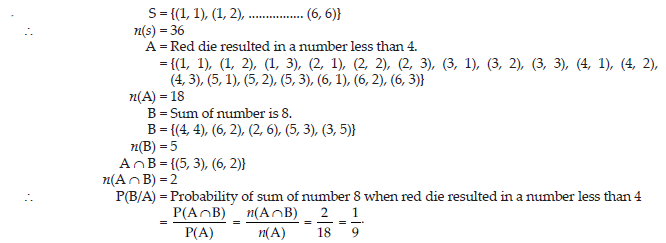
5. Find the direction cosines of the line, which is perpendicular to the lines whose direction consines are proportional to 1, – 1, 2 and 2, 1, – 1.
Answer:


6. A bag contains 5 green and 12 blue marbles. A second bag contains 7 green and 9 blue marbles. One marble is picked at random from the first bag and mixed up with marbles in the second bag. Then, a marble is randomly picked from it. Find the probability that the picked marble is green.
Answer:
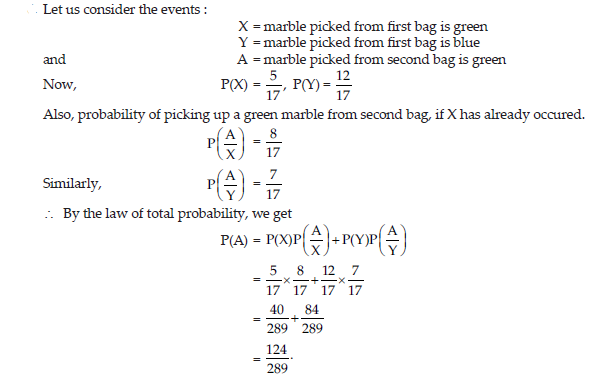
Section – B
7. Show that the direction consines of a vector equally inclined to the axes OX, OY and OZ are11/√3, 1/√3, 1/√3
Answer: Let a vector be equally inclined to axes OX, OY and OZ at angle a.
Then, the direction cosines of the vector are cos a, cos a and cos a.
Now, cos2a+cos2a+cos2a=1
⇒ 3cos2 a=1
cos a =1√3
Hence, the direction cosines of the vector which is equally inclined to the axes are 1/√3,1/√,1/√3
8. Find the value of λ, so that following lines are perpendicular to each other.
x +5/5λ+2=2-y/5 = 1-z/-1 and x/1=2y+1/4λ = 1-z/-3
OR
Find the distance between the point P(6, 5, 9) and the plane determined by the point A(3, – 1, 2),
B(5, 2, 4) and C(– 1, – 1, 6).
Answer: Given equation of lines are
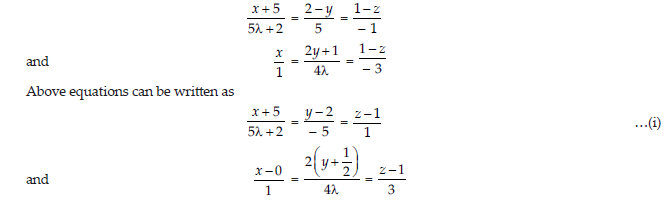
OR

9. Evaluate : ∫03/2|xcosπx|dx.
Answer:
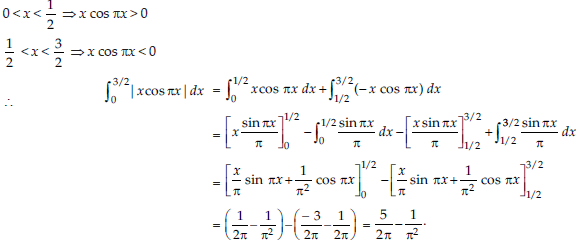
10. Find the general solution of the following differential equation :
xdy – (y + 2x2)dx = 0
OR
Find the particular solution of the differential equation.
dy/dx+ycotx=2x+x2cotx(x≠0),where y[π/2]=0
Answer:
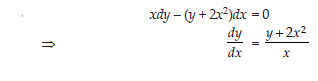

OR

Section – C
11. A person is known to speak lie 2 out of 5 times. He throws a die and report that it is a number greater than 3. Find the probability that it is actually a number greater than 3.
Answer: Let A be the event that a number greater than 3 and B be the event that a number is not greater than 3.
Sample space, S={1,2,3,4,5,6,}
Then, A={4,5,6} and B={1,2,3}
P(A)=P(Number greater than 3)
=3/6=1/2
12. Find the perpendicular distance of the point (2, 3, 4) from the line 4-x/2=y/6=1-z/3.Also, find coordinates of foot of perpendicular.
OR
Find the coordinates of the point where the line through the points (3, – 4, – 5) and (2, – 3, 1) crosses the plane determined by the points (1, 2, 3), (4, 2, – 3) and (0, 4, 3).
Answer:


13. Evaluate :∫01/2dx/(1+x2)√1-x2
Answer:


14. Two roads are to be constructed along the curve y2 = 2x and x2 = 2y which are intersected with each other. The common portion is to be covered by the green grass and planting colour flower plants
shown below :
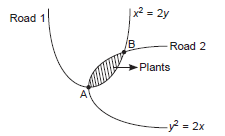
Attempt the following questions on the basis of the above case study :
(i) Find the points at which both the curves intersect with each other.
(ii) Which area is to be planted ?
Answer:


