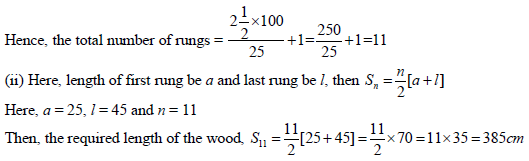Get Class 10 Mathematics Sample Papers free pdf download which is based on the latest pattern of CBSE and NCERT. It involves every one of the points given in NCERT Class 10 Mathematics book. You can easily download sample paper accounts Class 10 is given below.

Download 10th Mathematics Question paper in PDF free of charge. It will help you to make your preparation better to score higher marks in exams. These Class 10 Mathematics Sample Papers PDFs are prepared by our expert teacher.

This 10th Mathematics Question Paper PDF assists you with revising the complete chapter in minutes. One of the best tips suggested by teachers is Solving the sample papers during exam time.

We bring here the latest collection of Sample Papers for Class 10 Mathematics prepared as per the latest examination pattern issued by CBSE. Students can refer to the latest paper below available with answers and also download the suggested guess papers in PDF format for free. Students should solve the papers in exam type environment at home and then compare their results with the answers provided below. Students should regularly solve questions given in DK Goel Class 10 book and also solve the papers given below

Sample Paper Class 10 Mathematics Term 2 Set A

Sample Paper Class 10 Mathematics Term 2 Set A

SECTION – A

1. In the following, if PQ = 28 cm, then find the perimeter of ΔPLM.

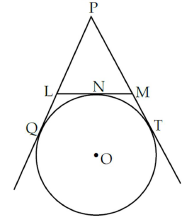
Answer : ∵ PQ = PT
⇒ PL + LQ = PM + MT
⇒ PL + LN = PM + MN (∵ LQ = LN, MT = MN) (Tangents to a circle from a common point)
Perimeter (ΔPLM) = PL + LM + PM
= PL + LN + MN + PM
= 2(PL + LN) = 2(PL + LQ) = 2 × 28 = 56 cm

2. Sum of the areas of two squares is 468 m2. If the difference of their perimeters is 24 m, formulate the quadratic equation to find the sides of the two squares.
Answer : Let the length of each side of a square be x m.
Then, its perimeter is 4x m.
It is given that the difference of the perimeters of two squares is 24 m.
∴ Perimeter of second square = (24 + 4x) m
⇒ Length of each side of second square = (24 + 4x) / 4 = 6 + x
It is given that the sum of the areas of two squares is 468 m².
∴ x² + (6 + x)² = 468 ⇒ x² + (36 + 12x + x²) = 468
⇒ 2x² + 12x – 432 = 0 ⇒ x² + 6x – 216 = 0
This is the required quadratic equation.

3. From a solid right circular cylinder of height 14 cm and base radius 6 cm, a right circular cone of same height and same base removed. Find the volume of the remaining solid.
Answer : Given, Height (h) = 14 cm, Base radius (r) = 6 cm
Volume of the remaining solid
= Volume of a right circular cylinder – Volume of a right circular cone

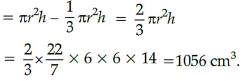
OR

A solid is in the shape of a cone surmounted by a hemisphere, the radius of each of them being 3.5 cm and the total height of solid is 9.5 cm. Find the volume of the solid.
Answer : Radius of cone (r) = Radius of hemisphere (r)= 3.5 cm
Total height of solid = 9.5 cm
∴ Height of cone (h) = 9.5 – 3.5 = 6 cm
Volume of solid = Volume of cone + Volume of hemisphere

4. Compute the mode for the following frequency distribution:

Answer : Here, modal class=12 – 16

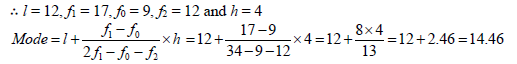
5. The first and the last terms of an A.P. are 8 and 65 respectively. If the sum of all its terms is 730, find its common difference.
Answer : Let a and d be the first term and common difference respectively of the A.P.
Given, a = 8 and l = 65 = a + (n – 1)d
⇒ 65 = 8 + (n – 1)d ⇒ 57 = (n – 1)d …(i)
Also, S_n = 730 ⇒ (n/2)(a+l) 730
⇒ n[8 + 65] = 1460
⇒ n = 1460/73 = 20
Putting value of n in (i), we get 57 = (20 – 1)d
⇒ 57 = 19d ⇒ d = 3

6. A polygon of n sides has n(n-3)/2 diagonals. How many sides a polygon has with 54 diagonals ?
Answer : Given, when number of sides is n, then the number of diagonals is n(n-3)/2
It is given that the number of diagonals = 54
⇒ n(n-3)/2 = 54 ⇒ n2 – 3n = 108
⇒ n² – 3n – 108 = 0 ⇒ n² – 12n + 9n – 108 = 0
⇒ n(n – 12) + 9(n – 12) = 0 ⇒ (n – 12)(n + 9) = 0
⇒ n = 12 or n = –9 ⇒ n = 12
(∵ n ≠ –9, as number of sides cannot be negative)
∴ The number of sides of the polygon is 12.

OR

For what values of k, the given quadratic equation 9x² + 6kx + 4 = 0 has equal roots?
Answer : Given, 9x² + 6kx + 4 = 0.
Comparing with ax² + bx + c = 0, we get a = 9, b = 6k, c = 41
Since, Discriminant, D = b² – 4ac
For equal roots, D = 0 we have b² – 4ac = 0 ⇒ (6k)² – 4 × 9 × 4 = 0
⇒ 36k² – 144 = 0 ⇒ 36k² = 144 ⇒ k2 = 4 ⇒ k = ± 2

SECTION – B

7. The median of the following data is 525. Find the values of x and y , if total frequency is 100 :

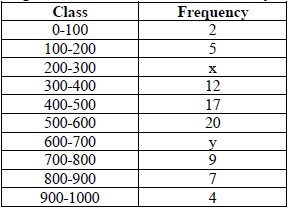
Answer :

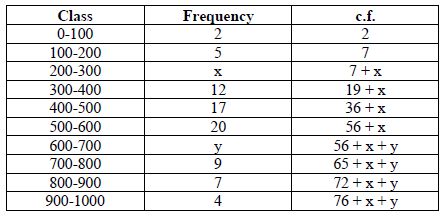
From table we have 76 + x + y = 100
x + y = 100 – 76 = 24 ……….(1)
Here median is 525 which lies between class 500 – 600.
Thus median class is 500-600.

Substituting the value of z is equation (1), we get
y = 24 – 9 = 15

8. The ratio of the length of a vertical rod and the length of its shadow is 1 : √3 . Find the angle of elevation of the Sun at that moment?
Answer : Let AB be a vertical rod and BC be its shadow.

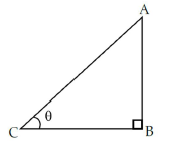
From the figure, ∠ACB = θ.
In ΔABC, ∠B = 90°, tanθ = AB/BC ⇒ tanθ = 1/√3 [ ∵ AB/BC = 1/√3 ]
⇒ tanθ = tan 30° ⇒ θ = 30°
Hence, the angle of elevation of the Sun is 30°.

9. Draw a line segment of length 6 cm. Using compasses and ruler, find a point P on it which divides it in the ratio 3 : 4.
Answer : Steps of construction:
Step-I : Draw a line segment AB of length 6 cm and draw a ray AX making an acute angle with this line segment AB.
Step-II : Locate 7 points, A₁, A₂, A₃, A₄, A₅, A₆, A₇ on AX such that AA₁ = A₁A₂ = A₂A₃ and so on.
Step-III : Join BA₇.
Step-IV : Through the point A₃, draw a line parallel to BA₇ intersecting AB at point P.
Thus, P is the point that divides line segment AB of length 6 cm in the ratio 3 : 4.

OR

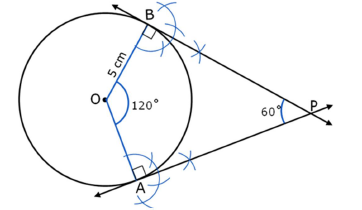
Draw a pair of tangents to a circle of radius 5 cm which are inclined to each other at an angle of 60°.
Answer : Steps of construction:
Step-I : Draw a circle of radius 5 cm with centre O.
Step-II : At O construct radii OA and OB such that ∠AOB = 120°.
Step-III : Draw perpendiculars at A and B such that these perpendiculars intersect at P.
Hence, PA and PB are required tangents.

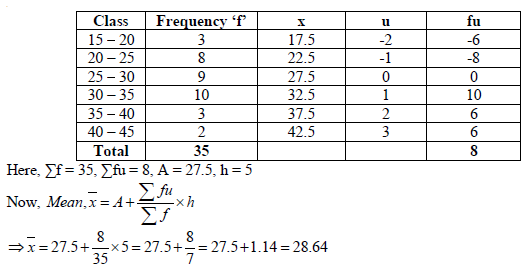
10. Find the arithmetic mean of the following frequency distribution:

Answer : 

SECTION – C

11. A solid is in the shape of a cone mounted on a hemisphere of same base radius. If the curved surface areas of the hemispherical part and the conical part are equal, then find the ratio of the radius and the height of the conical part.
Answer : Let ABC be a cone, which is mounted on a hemisphere.

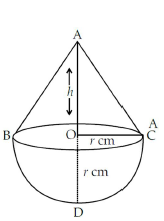
Given, OC = OD = r cm
Curved surface area of the hemispherical part = 2πr²
Slant height of a cone, l = √(r² + h²)
and curved surface area of a cone = πrl = πr √(r² + h²)
According to the problem, 2πr² = πr √(r² + h²) ⇒ πr = √(r² + h²)
on squaring both of the sides, we get 4r² = h² + r²
⇒ 4r² – r² = h² ⇒ r² = h²
⇒ r²/h² = 1/3 ⇒ r/h = 1/√3
Hence, the ratio of the radius and the height of conical part = 1 : √3.

OR

Water is flowing at the rate of 2.52 km/h through a cylindrical pipe into a cylindrical tank, the radius of whose base is 40 cm. If the increase in the level of water in the tank, in half an hour is 3.15 m, find the internal diameter of the pipe.
Answer : Rate of flow of water = 2.52 km/h = (2.52 × 1000 × 100) / (60×60) = 70 cm/s
In 1s, water flows = 70 cm
In 30 min, water flows = 70 × 30 × 60 cm = 126000 cm = h₁ (say)
Let internal radius of pipe = r¹
Height of water level in the tank in half an hour, h₂ = 3.15 × 100 = 315 cm
Radius of tank, r² = 40 cm
Volume of water flows from the cylindrical pipe in half an hour = Volume of water in cylindrical tank

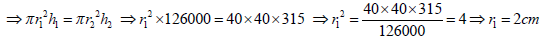
∴ Internal diameter of pipe = 2r₁ = 4 cm

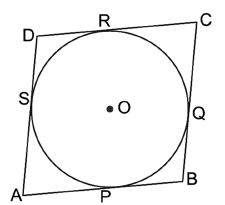
12. Prove that the parallelogram circumscribing a circle is a rhombus.
Answer : Let ABCD be a parallelogram such that its sides touch a circle with centre O.
We know that the tangents to a circle from an exterior point are equal in length.
Therefore, we have AP = AS (Tangents from A) … (i)
BP = BQ (Tangents from B) … (ii)
CR = CQ (Tangents from C) … (iii)
And DR = DS (Tangents from D) … (iv)
Adding (i), (ii), (iii) and (iv), we have
(AP + BP) + (CR + DR) = (AS + DS) + (BQ + CQ)
AB + CD = AD + BC
AB + AB = BC + BC (∵ABCD is a parallelogram, ∴ AB = CD, BC = DA)
2AB = 2BC ⇒ AB = BC
Thus, AB = BC = CD = AD
Hence, ABCD is a rhombus.

CASE STUDY- 1

13. A circus artist is climbing from the ground along a rope stretched from the top of a vertical pole and tied at the ground. The height of the pole is 12 m and the angle made by the rope with ground level is 30°.

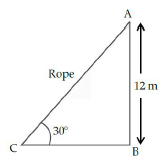
Give answer of the following questions:
(i) Find the distance covered by the artist in climbing the top of the pole.
(ii) Calculate the length of BC.
Answer : (i) Clearly, distance covered by the artist is equal to the length of the rope AC.
Let AB be the vertical pole of height 12 m.
It is given that ∠ACB = 30°
Thus, in right-angled triangle ABC, sin 30° = AB/AC ⇒ 1/2 = 12/AC ⇒ AC = 24m
(ii) In ΔABC, ∠B = 90°
tan 30° = AB/BC ⇒ 1/(√3) = 12/BC ⇒ BC = 12√3m

CASE STUDY – 2

14. A ladder has rungs 25 cm apart. (see the figure).

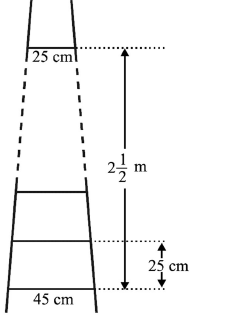
The rungs decrease uniformly in length from 45 cm at the bottom to 25 cm at the top. The top and the bottom rungs are 2½ m apart.
(i) Find the number of the rungs.
(ii) What is the length of the wood required for the rungs
Answer : (i) The distance between the two rungs is 25 cm.