Get Class 11 Mathematics Sample Papers free pdf download which is based on the latest pattern of CBSE and NCERT. It involves every one of the points given in NCERT Class 11 Mathematics book. You can easily download sample paper accounts Class 11 is given below.

Download 11th Mathematics Question paper in PDF free of charge. It will help you to make your preparation better to score higher marks in exams. These Class 11 Mathematics Sample Papers PDFs are prepared by our expert teacher.

This 11th Mathematics Question Paper PDF assists you with revising the complete chapter in minutes. One of the best tips suggested by teachers is Solving the sample papers during exam time.

We bring here the latest collection of Sample Papers for Class 11 Mathematics prepared as per the latest examination pattern issued by CBSE. Students can refer to the latest paper below available with answers and also download the suggested guess papers in PDF format for free. Students should solve the papers in exam type environment at home and then compare their results with the answers provided below. Students should regularly solve questions given in DK Goel Class 11 book and also solve the papers given below

Sample Paper Class 11 Mathematics Term 2 Set A

Sample Paper Class 11 Mathematics Term 2 Set A

PART – A
Section – I

1. What is the value of cos (3π/2)c ?
(a) –1
(b) 0
(c) 1
(d) None of these

2. Solution of |3x – 2| ≥ 1 is
(a) [1/3,1]
(b) (1/3,1)
(c) {1/3,3}
(d) (-∞,1/3]∪[1, ∞)

3. If f(x) = x3+x2+1 /x , then f ′(x) =
(a) 2x+1-/1/x2
(b) x+1+1/2
(c) 2x-3-1/x2
(d) None of these

4. Let S = {1, 2, 3, 4, 5, 6} and E = {1, 3, 5}, then E′ or E is
(a) {2, 4}
(b) {3, 6}
(c) {1, 2, 4}
(d) {2, 4, 6}

Section – II

Case study-based question is compulsory. Attempt any 4 sub parts. Each sub-part carries 1 mark.
5. On Sunday, Gautam and Gaurav were getting bore. They decided to play with cards. While playing cards, Gaurav asked Gautam to choose 4 cards from the pack of 52 cards.

Based on the above information, answer the following questions.

(i) In how many ways Gautam can select all the four cards from same suit?
(a) 1980
(b) 2860
(c) 2530
(d) 789

(ii) In how many ways Gautam can select all the four cards from different suits?
(a) 154
(b) 1690
(c) 13921
(d) 134

(iii) In how many ways, Gautam can select all face cards?
(a) 532
(b) 729
(c) 339
(d) 495

(iv) In how many ways, Gautam can select two red cards and two black cards?
(a) 3252
(b) 4252
(c) 2252
(d) 1252

(v) In how many ways, Gautam can select cards of same colour.
(a) 20900
(b) 27000
(c) 29900
(d) 29000

PART – B
Section – III

6. If 1/8! + 1/9! = 1/10! , then find x.
Answer: Given, 1/8! + 1/9! = x/10! ⇒ 10!/8! + 10!/9! = x
⇒ 10 × 9 + 10 = x ⇒ x = 100

7. If a point lies in xy-plane, then what is its z-coordinate?
Answer: If a point lies in xy-plane, then its z-coordinate is 0.

8. What is the eccentricity of the hyperbola 18y2 – 6x² = 36 ?
Answer: Given 18y2 – 6x² = 36 ⇒ y²/2 – x2/6 = 1
⇒ a² = 2, b² = 6
∴ Eccentricity, e = √a²+b²/a² = √2+6/2 = √8/2 = 2 .

OR

Write equation of the parabola whose vertex is (0, 0) and focus is (0, –4).
Answer: Focus is (0, –4) ⇒ a = 4.
∴ Equation of parabola, x2 = –4ay ⇒ x2 = – 16y.

9. Evaluate : d/dx sinn x.
Answer: d/dx(sinn x) = d/dx(sin x)n
= n (sin x)n-1.d/dx (sin x)
∴ d/dx (sinn x)= n(sinn−1 x).cos x

10. Find the derivative of √sec 2x-1/sec 2x+1 .√z
Answer: Let y = √sec2x – 1/sec2x + 1= √1 – cos2x/1 + cos2x = √2sin2 x/2cos2 x = tan x
⇒ dy/dx = sec2 x

Section – IV

11. Find the point on y-axis which is at a distance of √10 units from the point (1, 2, 3).
Answer: Let P be a point on y-axis. Therefore, it is of the form P(0, y, 0).
The point (1, 2, 3) is at a distance of 10 units from
P(0, y, 0).
⇒ √(1− 0)2 +(2 − y)2 +(3 − 0)2 = 10
⇒ y2 – 4y + 4 = 0 ⇒ (y – 2)2 = 0 ⇒ y = 2
Hence, the required point is P(0, 2, 0).

12. Find the value of n such that ⁿP₅ = 42ⁿP₃, n > 4 .
Answer: We have nP5 = 42 nP3
⇒ n(n – 1) (n – 2) (n – 3) (n – 4) = 42 n(n – 1) (n – 2)
⇒ (n – 3) (n – 4) = 42
[Since n > 4, so n(n – 1) (n – 2) ≠ 0]
⇒ n2 – 7n – 30 = 0 ⇒ n2 – 10n + 3n – 30 = 0
⇒ (n – 10) (n + 3) = 0 ⇒ n – 10 = 0 or n + 3 = 0
⇒ n = 10 or n = – 3
Since n cannot be negative, so n = 10

OR

In how many ways can 4 red, 3 yellow and 2 green discs can be arranged in a row if the discs of the same colour are indistinguishable?
Answer:Total number of discs are 4 + 3 + 2 = 9. Out of 9 discs, 4 are of the first kind (red), 3 are of the second kind (yellow) and 2 are of the third kind (green).
Therefore, the number of arrangements = 9!/4!3!2! = 1260

13. The team of medical students doing their internship have to assist during surgeries at a city hospital.
The probabilities of surgeries rated as very complex, complex, routine, simple or very simple are 0.15, 0.20, 0.31, 0.26 and 0.08 respectively. Find the probabilities that a particular surgery will be rated as complex or very complex.
Answer: Let A, B, C, D and E be the event that surgeries are rated as very complex, complex, routine, simple or very simple, respectively
∴ P(A) = 0.15, P(B) = 0.20, P(C) = 0.31, P(D) = 0.26 and P(E) = 0.08
∴ P(complex or very complex) = P(A or B)
= P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= 0.15 + 0.20 – 0 [ P(A ∩ B) = 0]
= 0.35

14. Find the value of 1+cosθ + sinθ/1- cosθ + sinθ .
Answer: We have, 1+cos θ + sin θ/1-cos θ + sin θ
= 2cos2(θ/2) + 2sin (θ/2).cos(θ/2)/2sin2(θ/2) + 2sin (θ/2).cos(θ/2)
= 2 cos(θ/2)[cos(θ/2) + sin(θ/2)]/2 sin(θ/2)[sin(θ/2) + cos(θ/2)] = cot(θ/2)

Section – V

15. Find the solution of |2x – 3| < |x + 2|.
Answer: Consider |2x – 3| < |x + 2|
⇒ –|x + 2|< 2x – 3 < |x + 2| …(1)
Case I : x + 2 ≥ 0. Then from (1), we have
–(x + 2) < 2x – 3 < x + 2 ⇒ –x – 2 < 2x – 3 < x + 2
⇒ 1 < 3x and x < 5 ⇒ 1/3 < x < 5.
Case II : x + 2 < 0. Then from (1), we have
(x + 2) < 2x – 3 < – (x + 2)
⇒ – (x + 2) > 2x – 3 > (x + 2)
⇒ 1 > 3x and x > 5
⇒ 1/3 > x and x > 5, which is not possible.

16. If f(x) = 5sin x – 9cos x + 2×2 + 3, then find f ′(x).
Answer: Given f(x) = 5sin x – 9cosx + 2×2 + 3
Now, f(x) = df(x)/dx = d/dx [5sin x – 9cosx + 2×2 + 3]
= 5d/dx(sin x) – 9d/dx (cos x) + 2d/dx (x2) + 3 = 5 cos x + 9 sin x + 4x

Answer:

For |x| < 1, if y = 1 + x + x2 + … ∞, then find the value of dy/dx .
Answer: We have, y = 1 + x + x2 + … ∞
It’s a G.P. with common ratio x and first term 1.
∴ y = 1/1-x [∴ |x| < 1] …(i)
∴ dy/dx = d/dx (1− x)−1 = (–1) (1 – x)2 (–1)
= 1/(1-x)2

17. A coin is tossed three times, consider the following events :
A : no head appear.
B : exactly one head appear.
C : atleast two heads appear.
Show that A, B and C form a set of mutually exclusive and exhaustive events.
Answer: The sample space of the experiment is
S = {HHH, HHT, HTH, THH, HTT, THT, TTH, TTT}
Clearly, A = {TTT}, B = {HTT, THT, TTH} and C = {HHT, HTH, THH, HHH}
Now, A ∪ B ∪ C = {TTT, HTT, THT, TTH, HHT, HTH, THH, HHH} = S
Therefore, A, B and C are exhaustive events.
Also A ∩ B = f, A ∩ C = f and B ∩ C = Φ
Therefore, the events are pair-wise disjoint, i.e., they are mutually exclusive.
Hence, A, B and C form a set of mutually exclusive and exhaustive events.

Section – VI

18. If A + B + C = 180°, then find the value of sin2 A/2 + sin2 B/2 + sin2 C/2 .
Answer:

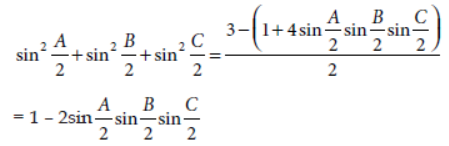
OR

If sin⁴ θ/a + cos⁴ θ/b = 1/a+b , then find the value of sin¹² θ/a⁵ + cos¹² θ/b5 .
Answer: Given, sin⁴ θ /a + cos⁴θ/b = 1/a+b
⇒ (sin² θ)²/a + (1-sin² θ)² /2 = 1/a+b
⇒ λ²b(a + b) + (a + b) a (1 – λ)2 = ab, where λ = sin²q
⇒ λ²ab + λ²b² + a² + a2λ² – 2a²λ + ab + abλ² – 2abλ = ab
⇒ λ2{a² + b² + 2ab} + a² – 2λa (a + b) = 0
⇒ {λ(a + b)}² + a² – 2λa (a + b) = 0
⇒ {λ(a + b) – a}² = 0
⇒ λ = a/a+b ⇒ sin2θ = a/a+b …(i)
From (i), cos²θ = 1 – sin²θ = 1 – a/a+b = b/a+b
Using (i) and (ii), we get
sin12θ /a⁵ + cos12θ/b⁵ = (sin² θ)6/a⁵ + (cos² θ)⁶/b⁵
= (a/a+b)⁶/a⁵ + (b/(a+b)⁶/b⁵ = a+b/(a+b)6 = 1/(a+b)⁵

19. Find the equation of a circle passing through the point (7, 3) having radius 3 units and whose centre lies on the line y = x – 1.
Answer: Consider the equation of the circle is
(x – h)² + (y – k)2 = r2
⇒ (x – h)² + (y – k)² = 9 … (i)
Since, centre (h, k) lies on the line
y = x – 1 i.e, k = h – 1 … (ii)
Since the circle passes through the point (7, 3), then
(7 – h)² + (3 – k)2 = 9 … (iii)
⇒ h² + k² – 14h – 6k + 49 = 0
Substituting (ii) in (iii), we get
h2 + (h – 1)² – 14h – 6(h – 1) + 49 = 0
⇒ h² + h² – 2h + 1 – 14h – 6h + 6 + 49 = 0
⇒ 2h² – 22h + 56 = 0
⇒ h² – 11h + 28 = 0
⇒ (h – 7)(h – 4) = 0 ⇒ h = 4, 7
When h = 7, then k = 7 – 1 = 6 (from (ii))
∴ Centre (7, 6)
When h = 4, then k = 3
∴ Centre = (4, 3)
Hence the required equation of circle having centre
(7, 6) is
(x – 7)2 + (y – 6)2 = 9
⇒ x2 + y2 – 14x – 12y + 76 = 0
When centre (4, 3) then the equation of the circle is
(x – 4)2 + (y – 3)2 = 9
⇒ x2 + y2 – 8x – 6y + 16 = 0

OR

Find the equation of the ellipse which passes through the point (–3, 1) and has eccentricity √2/5, with x-axis as its major axis and centre at the origin.
Answer: Let x2/a2 + y2/b2 = 1 be the equation of the ellipse passing through the point (–3, 1), a > b.
Therefore, we have 9/a2 + 1/b2 = 1
⇒ 9b2 + a2 = a2b2 ⇒ 9a2(1 – e2) + a2 = a2a2 (1 – e2)
⇒ a2 = 32/3
Again, b2 = a2(1 – e2) = 32/3(1-2/5) = 32/5
Hence, the required equation of the ellipse is
x2/32/3 + y2/32/5 = 1 or 3×2 + 5y2 = 32