Please refer to below Exam Question for Class 12 Mathematics Chapter 1 Relations and Functions. These questions and answers have been prepared by expert Class 12 Mathematics teachers based on the latest NCERT Book for Class 12 Mathematics and examination guidelines issued by CBSE, NCERT, and KVS. We have provided Class 12 Mathematics exam questions for all chapters in your textbooks. You will be able to easily learn problems and solutions which are expected to come in the upcoming class tests and exams for standard 10th.

Chapter 1 Relations and Functions Class 12 Mathematics Exam Question

All questions and answers provided below for Exam Question Class 12 Mathematics Chapter 1 Relations and Functions are very important and should be revised daily.

Exam Question Class 12 Mathematics Chapter 1 Relations and Functions

Very Short Answer Type Questions

Question. If f(x) = x + 7 and g(x) = x – 7, x ∈ R, find (fog) (7).
Answer. f(x) = x + 7 and g(x) = x – 7
So, fog (x) = f(g(x)) = f (x – 7) = x – 7 + 7 = x
⇒ fog (x) = x
∴ fog (7) = 7

Question. If f : R → R is defined by
f(x) = x² – 3x + 2, find f(f(x)).
Answer. f(f(x)) = f (x² – 3x + 2)
= (x² – 3x + 2)² – 3 (x² – 3x + 2) + 2
= x⁴ + 9x² + 4 – 6x³ – 12x + 4x² – 3x² + 9x – 6 + 2
= x⁴ – 6x³ + 10x² – 3x.

Question. Let * be a binary operation on the set of all non-zero real numbers, given by a * b = ab/5 for all a, b ∈ R – {0}. Find the value of x, given that 2 * (x * 5) = 10.
Answer.

Question. Let * : R × R → R, given by (a, b) → a + 4b² is a binary operation. Compute (– 5) * (2 * 0).
Answer. Here * : R × R → R is given by
a * b = a + 4b².
(–5) * (2 * 0) = (–5) * (2 + 4.02) = – 5 * (2)
= – 5 + 4.2² = – 5 + 16 = 11

Question. Let A = {1, 2, 3}, B = {4, 5, 6, 7} and let f = {(1, 4), (2, 5), (3, 6)} be a function from A to B, state whether f is one-one or not.
Answer. A = {1, 2, 3}, B = {4, 5, 6, 7} and
f = {(1, 4), (2, 5), (3, 6)}
We have, f(1) = 4, f(2) = 5 and f(3) = 6. Distinct
elements of A have distinct images in B. Hence, f is a one-one function.

Question. What is the range of the function

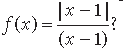
Answer.

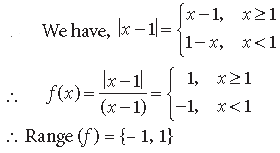
Question. Let * be a binary operation on N given by a * b = L.C.M. (a, b) for all a, b ∈ N. Find 5 * 7.
Answer. 5 * 7 = L.C.M. (5, 7) = 35.

Question. The binary operation * : R × R → R, is defined as a * b = 2a + b. Find (2 * 3) * 4.
Answer. * : R × R ∈ R given by
a * b = 2a + b
∴ (2 * 3) * 4 = (2 × 2 + 3) * 4 = 2 × 7 + 4 = 18.

Question. If the binary operation * on the set of integers Z, is defined by a * b = a + 3b², then find the value of 8 * 3.
Answer. Here a * b = a + 3b2 ∀a, b ∈ Z
⇒ 8 * 3 = 8 + 3.32 = 8 + 27 = 35.

Question. Let * be a binary operation defined on the set of integers by a * b = 2a + b – 3. Find 3 * 4.
Answer. Here a * b = 2a + b – 3
∴ 3 * 4 = 2(3) + 4 – 3 = 7

Short Answer Type Questions

Question. Let A = {1, 2, 3, …, 9} and R be the relation in A × A defined by (a, b) R (c, d) if a + d = b + c for (a, b), (c, d) in A × A. Prove that R is an equivalence relation. Also obtain the equivalence class [(2, 5)].
Answer. Given A = {1, 2, 3, 4,…,9} ⊂ N, the set of natural numbers.
To show : R is an equivalence relation.
(i) Reflexivity : Let (a, b) be an arbitrary element of
A × A. Then, we have (a, b) ∈ A × A ⇒ a, b ∈ A
⇒ a + b = b + a
(by commutativity of addition on A ⊂ N)
⇒ (a, b) R (a, b)
Thus, (a, b) R (a, b) for all (a, b) ∈ A × A
So, R is reflexive.
(ii) Symmetry: Let (a, b), (c, d) ∈ A × A such that
(a, b) R (c, d) ⇒a + d = b + c ⇒ b + c = a + d
⇒ c + b = d + a
(by commutativity of addition on A ⊂ N)
⇒ (c, d) R (a, b).
Thus, (a, b) R (c, d)
⇒ (c, d) R (a, b) for all (a, b), (c, d) ∈ A × A.
So, R is symmetric.
(iii) Transitivity: Let (a, b), (c, d), (e, f) ∈ A × A such
that (a, b) R (c, d) and (c, d) R (e, f)
Now, (a, b) R (c, d) ⇒ a + d = b + c                 …(i)
and (c, d) R (e, f) ⇒ c + f = d + e                    …(ii)
Adding (i) and (ii), we get
(a + d) + (c + f) = (b + c) + (d + e)
⇒ a + f = b + e ⇒ (a, b) R (e, f)
Thus, (a, b) R (c, d) and (c, d) R (e, f) ⇒ (a, b) R (e, f).
So, R is transitive.
∴ R is an equivalence relation.
Equivalence class for [(2, 5)] is {(1, 4), (2, 5), (3, 6), (4, 7), (5, 8) (6, 9)}.

Question. Let f : X → Y be a function, define a relation R on X given by R = {(a, b) : f (a) = f (b)}. Show that R is an equivalence relation on X.
Answer. We have, f : X → Y is a function
R = {(a, b) : f(a) = f(b)}
(i) Reflexivity : For any a ∈ X, we have
f(a) = f(a) ⇒ (a, a) ∈ R ⇒ R is reflexive.
(ii) Symmetric : For any a, b ∈ X,
Let (a, b) ∈ R ⇒ f(a) = f(b)
⇒ f(b) = f(a) ⇒ (b, a) ∈ R
So, R is symmetric.
(iii) Transitive : For any a, b, c ∈ X,
Let (a, b) ∈ R and (b, c) ∈ R
⇒ f(a) = f(b) and f(b) = f(c)
⇒ f(a) = f(c) ⇒ (a, c) ∈ R
So, R is transitive.
Hence, R is an equivalence relation on X.

Question. Prove that the relation R in the set A = {1, 2, 3, 4, 5} given by R = {(a, b) : |a – b| is even}, is an equivalence relation
Answer. We have A = {1, 2, 3, 4, 5}
R = {(a, b) : |a – b| is even}; a, b ∈ A
(i) Reflexive : For any a ∈ A,
We have |a – a| = 0, which is even.
⇒ (a, a) ∈ R ∀ a ∈ A
So, R is reflexive.
(ii) Symmetric : For any a, b ∈ A,
Let (a, b) ∈ R ⇒ |a – b| is even ⇒ |b – a| is even
⇒ (b, a) ∈ R.
So, R is symmetric.
(iii) Transitive : For any a, b, c ∈ A. Let (a, b) ∈ R and
(b, c) ∈ R
⇒ |a – b| is even and |b – c| is even
⇒ a – b = ± 2k₁ and b – c = ± 2k₂, for k₁, k₂ ∈ N
⇒ (a – b) + (b – c) = ± (2k₁ + 2k₂); k₁, k₂ ∈ N
⇒ a – c = ± 2(k₁ + k₂); k₁, k₂ ∈ N
⇒ |a – c| is even ⇒ (a, c) ∈ R
Thus, (a, b) ∈ R and (b, c) ∈ R ⇒ (a, c) ∈ R
So, R is transitive.
Hence, R is an equivalence relation.

Question. If f : R → R be the function defined by
f(x) = 4x³ + 7, show that f is a bijection.
Answer. Here, f(x) = 4x³ + 7
Let x₁, x₂ ∈ R s.t.

Question. Show that the function f : R → R given by f(x) = ax + b, where a, b ∈ R, a ≠ 0 is a bijective function.
Answer. We have f (x) = ax + b where a, b ∈ R and a ≠ 0
(i) Injectivity : Let x₁, x₂ ∈ R such that f (x1) = f (x₂)
⇒ ax1 + b = ax₂ + b ⇒ x₁ = x₂
∴ f(x) is one-one.
(ii) Surjectivity : Let y ∈ R (co-domain) such that
f(x) = y

Question. If the function f : R → R be given by f(x) = x² + 2 and g : R → R be given by

find fog and gof and hence find fog (2) and gof (–3).
Answer. Here f : R → R s.t. f(x) = x² + 2

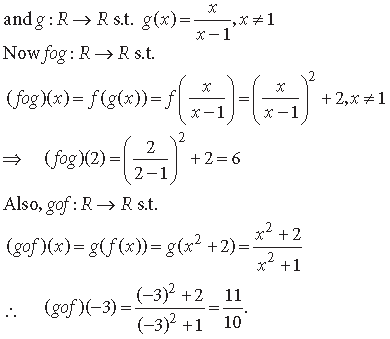
Question. Let A = R – {3}, B = R – {1}. Let f : A → B be defined by

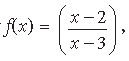
for all x ∈ A. Then show that f is bijective. Hence find f^–1(x).
Answer. A = R – {3}; B = R – {1}
and f : A → B defined as

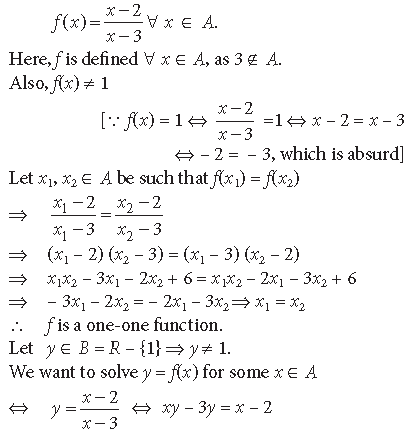
Question. Let f, g : R → R be two functions defined as f(x) = |x| + x and g(x) = |x| – x, for all x ∈ R. Then find fog and gof.
Answer. Here, f, g : R → R s.t.

Question.

Answer.

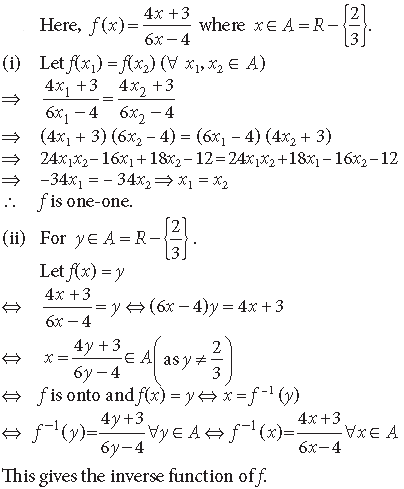
Question. Consider f : R₊ → [4, ∞) given by f(x) = x² + 4. Show that f is invertible with the inverse f ^–1 of f given by f⁻¹(y) = √y − 4, where R₊ is the set of all non-negative real numbers.
Answer. f : R₊ → [4, ∞) given by f(x) = x₂ + 4
(i) Let x₁, x₂ ∈ R+ s.t. f(x₁) = f(x₂)
⇒ x₁² + 4 = x₂² + 4 ⇒ x₁₂ = x₂²
⇒ x₁ = x₂                  (∵ x₁, x₂ ∈ R+)
⇒ f is one-one

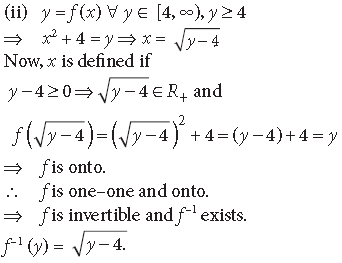
Question. Let A = R – {2} and B = R – {1}. If f : A → B is a function defined by

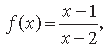
show that f is one-one and onto. Hence find f^–1.
Answer.

Question. Let f : R → R be defined as f (x) = 10x + 7. Find the function g : R → R such that gof = fog = I_R.
Answer. Let y ∈ R (co-domain) be arbitrary.
By definition, y = 10x + 7 for x ∈ R

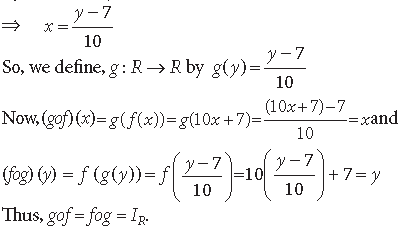
Question. If the function f : R → R is given by

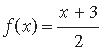
and g : R → R is given by g(x) = 2x – 3. Find
(i) fog and (ii) gof. Is f^–1 = g?
Answer.

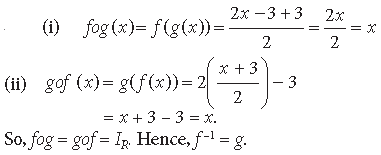
Question. If f : R → R and g : R → R are defined respectively as f (x) = x² + 3x + 1 and g(x) = 2x – 3. Find (a) fog (b) gof.
Answer. (a) fog (x) = f (g(x)) = (2x – 3)² + 3(2x – 3) + 1
= 4x² – 12x + 9 + 6x – 9 + 1 = 4x² – 6x + 1
(b) gof (x) = g(f(x)) = 2(x² + 3x + 1) – 3
= 2x² + 6x + 2 – 3 = 2x² + 6x – 1

Question. If f be a greatest integer function and g be an absolute value function, find the value of

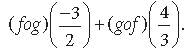
Answer. Here f(x) = [x] and g(x) = |x|
fog (x) = f(g(x)) = f(|x|) = [|x|]

Question. Let S be the set of all rational numbers except 1 and * be defined on S by a * b = a + b – ab, for all a, b ∈ S.
Prove that
(i) * is a binary operation on S.
(ii) * is commutative as well as associative.
Answer. We have, S = Q – {1}
a * b = a + b – ab ∀ a, b ∈ S
(i) As a, b ∈ S ⇒ a, b ∈ Q and a ≠ 1, b ≠ 1, …(1)
∴ a + b – ab ∈ Q
We check : a + b – ab ≠ 1
Suppose a + b – ab = 1
⇒ a + b – ab – 1 = 0
⇒ a – 1 + b (1 – a) = 0
⇒ –(1 – a) + b (1 – a) = 0
⇒ (1 – a) (– 1 + b) = 0
⇒ Either 1 – a = 0 or – 1 + b = 0
⇒ a = 1 or b = 1
This contradicts (1).
∴ a + b – ab ≠ 1.
⇒ a + b – ab ∈ Q – {1} = S
⇒ * is binary operation on S.
(ii) Let a, b ∈ S
a * b = a + b –a·b = b + a – b·a = b * a * is commutative in S
Let a,b,c ∈ S
Then a * (b * c) = a * (b + c – bc)
= a + b + c – bc – a(b + c – bc)
= a + b + c – ab – bc – ca + abc
= a + b – ab + c – (a + b – ab) c
= (a * b) * c
∴ * is associative

Question. Consider the binary operations * : R × R → R and o : R x R → R defined as a * b = |a – b| and a o b = a for all, a, b ∈ R. Show that ‘*’ is commutative but not associative, ‘o’ is associative but not commutative. 
Answer. b * a = |b – a| = |a – b| [Q |–x| = |x| ∀x ∈ R]
= a * b ∀ a, b ∈ R
⇒ * is commutative on R.
Also, for a = 2, b = 4, c = 5
(a * b) * c = (2 * 4) * 5 = |2 – 4| * 5
= 2 * 5 = |2 – 5| = 3
and a * (b * c) = 2 * (4 * 5) = 2 * |4 – 5|
= 2 * 1 = |2 – 1| = 1.
∴ (a * b) * c ≠ a * (b * c)
⇒ * is not associative on R.
Also, (a o b) o c = a o c = a
and a o (b o c) = a o b = a
⇒ (a o b) o c = a o (b o c) ∀ a, b, c ∈ R
⇒ o is associative on R.
Also, for a = 3, b = 2
a o b = 3 o 2 = 3
b o a = 2 o 3 = 2
⇒ a o b ≠ b o a
⇒ o is not commutative on R.

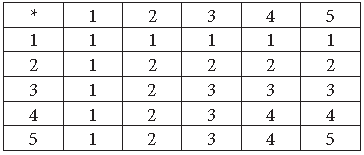
Question. Consider the binary operation * on the set {1, 2, 3, 4, 5} defined by a * b = min (a, b). Write the operation table of the operation *.
Answer. Let A = {1, 2, 3, 4, 5}
a * b = minimum of a and b

Question. A binary operation * on the set {0, 1, 2, 3, 4, 5} is defined as :

Show that zero is the identity for this operation and each element a ≠ 0 of the set is invertible with 6 – a being the inverse of a.
Answer.

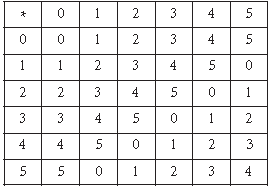
Identity : Let e be the identity element, then
a * e = a = e * a
Now, a * 0 = a + 0 = a and 0 * a = 0 + a = a
Thus, a * 0 = a = 0 * a. Hence, 0 is the identity element of the operation.
Inverse : Since, each row or column contains the identity element i.e., 0.
So, each element is invertible.
Now, a * (6 – a) = a + (6 – a) – 6 = 0
and (6 – a) * a = (6 – a) + a – 6 = 0.
Hence, each element a of the set is invertible with inverse 6 – a.

Question. Let * be a binary operation on Q defined by a * b = 3ab/5 Show that * is commutative as well as associative. Also, find its identity element, if it exists.
Answer.

Question. Let * be a binary operation on the set of rational numbers given as a * b = (2a – b)², a, b ∈ Q. Find 3 * 5 and 5 * 3. Is 3 * 5 = 5 * 3 ?
Answer. We have, a * b = (2a – b)²
∴ 3 * 5 = (2 × 3 – 5)² = (6 – 5)² = 1
5 * 3 = (2 × 5 – 3)² = (10 – 3)² = 49
Thus, 3 * 5 ≠ 5 * 3

Question. Let * be the binary operation on N given by a * b = L.C.M. of a and b. Find the value of 20 * 16. Is * (i) commutative, (ii) associative ?
Answer. We have, a * b = L.C.M. of a and b
∴ 20 * 16 = L.C.M. of 20 and 16 = 80
(i) Commutativity : a * b = L.C.M. of a and b
= L.C.M. of b and a = b * a
⇒ a * b = b * a
So, * is commutative.
(ii) Associativity : (a * b) * c
= [L.C.M. (a, b)] * c
= L.C.M. [L.C.M. (a, b), c]
= L.C.M. (a, b, c)
and a * (b * c) = a * [L.C.M. (b, c)]
= L.C.M. [a, L.C.M. (b, c)]
= L.C.M. (a, b, c)
⇒ a * (b * c) = (a * b) * c
So, * is associative.

Question. Let A = {a, b, c} and the relation R be defined on A as follows
R = {(a, a), (b, c), (a, b)}
Then, write minimum number of ordered pairs to be added in R to make R reflexive and transitive.
Answer. Given relation, R = {(a, a), (b, c), (a, b)}.
To make R is reflexive we must add (b, b)and (c, c) to R. Also, to make R is transitive we must add (a, c) to R.
So, minimum number of ordered pair is to be added are (b, b), (c, c), (a, c).

Question. Let D be the domain of the real valued function f defined by

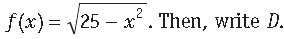
Answer.

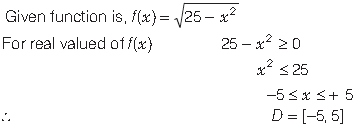
Question. If the mappings f and g are given by f = {(1, 2), (3, 5), (4, 1)} and g = {(2, 3), (5, 1), (1, 3)}, write fog.
Answer. Given that, f = {(1, 2), (3, 5), (4, 1)}
and g = {(2, 3), (5, 1), (1, 3)}
Now, fog(2) = f{g(2)} = f(3) = 5
fog(5) = f{g(5)} = f(1) = 2
fog(1) = f{g(1)} = f(3) = 5
fog = {(2, 5), (5, 2), (1, 5)}

Question. If functions f : A→ B and g : B → A satisfy gof = I_A , then show that f is one-one and g is onto.
Answer. Given that,

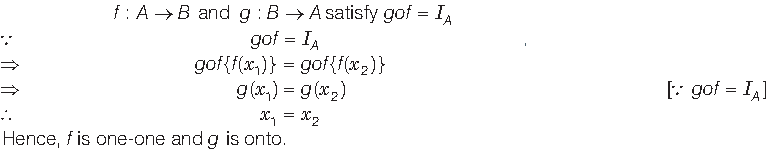
Question. Let X = {1, 2, 3} and Y = {4, 5}. Find whether the following subsets of X x Y are functions from X to Y or not.
(i) f = {(1, 4), (1, 5), (2, 4), (3, 5)} (ii) g = {(1, 4), (2, 4), (3, 4)}
(iii) h = {(1, 4), (2, 5), (3, 5)} (iv) k = {(1, 4), (2, 5)}
Answer. Given that, X = {1, 2, 3} and Y = {4, 5}
X x Y = {(1, 4), (1, 5), (2, 4), (2, 5), (3, 4), (3, 5)}
(i) f = {(1, 4), (1, 5), (2, 4), (3, 5)}
f is not a function because f has not unique image.
(ii) g = {(1, 4), (2, 4), (3, 4)}
Since, g is a function as each element of the domain has unique image.
(iii) h = {(1, 4), (2, 5), (3, 5)}
It is clear that h is a function.
(iv) k = {(1, 4), (2, 5)}
k is not a function as 3 has not any image under the mapping.

Question. Let the function f : R → R be defined by f (x) = cos x, ∀ x ∈ R. Show that f is neither one-one nor onto.
Answer. Given function, f(x) = cos x,  ∀ x ∈ R

So, f(x) is not one-one.
Now, f(x) = cos x, “x ÎR is not onto as there is no pre-image for any real number. Which does not belonging to the intervals [-1, 1], the range of cos x.

Question. Are the following set of ordered pairs functions? If so examine whether the mapping is injective or surjective.
(i) {(x, y) : x is a person, y is the mother of x}.
(ii) {(a, b) : a is a person, b is an ancestor of a}.
Answer. (i) Given set of ordered pair is {(x, y) : x is a person, y is the mother of x}.
It represent a function. Here, the image of distinct elements of x under f are not distinct, so it is not a injective but it is a surjective.
(ii) Set of ordered pairs = {(a, b) : a is a person, b is an ancestor of a} Here, each element of domain does not have a unique image. So, it does not represent function.

Question. Is g = {(1, 1), (2, 3), (3, 5), (4, 7)} a function? If g is described βy g(x) = ax + β, then what value should be assigned to a and β?
Answer. Given that, g = {(1, 1), (2, 3), (3, 5), (4, 7)}.
Here, each element of domain has unique image. So, g is a function.
Now given that, g(x) = ax + β
g(1) = a + β
a + β = 1                       …(i)
g(2) = 2a + β
2a + β = 3                    …(ii)
From Eqs. (i) and (ii),
2(1 – β) + β = 3
⇒ 2 – 2β + β = 3
⇒ 2 – β = 3
β = – 1
If β = – 1, then a = 2
a = 2, β =

Long Answer Type Questions

Question. If * be binary operation defined on R by a * b = 1 + ab, ∀ a, b ∈ R.
Then, the operation * is
(i) commutative but not associative.
(ii) associative but not commutative.
(iii) neither commutative nor associative.
(iv) both commutative and associative.
Answer. (i) Given that, a * b = 1 + ab, ∀ a, b ∈ R
a * b = ab + 1= b * a
So, * is a commutative binary operation.
Also, a * (b * c) = a * (1 + bc)= 1 + a(1 + bc)
a * (b * c) = 1 + a + abc                                         …(i)
(a * b) * c = (1 + ab) * c
= 1 + (1 + ab)c = 1 + c + abc                                 …(ii)
From Eqs. (i) and (ii),
a * (b * c) ¹ (a * b) * c
So, * is not associative
Hence, * is commutative but not associative

Question. Let * be the binary operation defined on Q. Find which of the following binary operations are commutative
(i) a * b = a – b, ∀ a, b ∈ Q
(ii) a * b = a² + b² ∀ a , , b ∈ Q
(iii) a * b = a + ab, ∀ a, b ∈ Q
(iv) a * b = (a – b)², ∀ a , b ∈ Q
Answer. Given that * be the binary operation defined on Q.
(i) a * b = a – b, ∀ a, b ∈ Q and b * a = b – a
So, a * b ¹ b * a                     [∵ b – a ¹ a – b]
Hence, * is not commutative.
(ii) a * b = a2 + b2
b * a = b2 + a2
So, * is commutative.                                           [since, ‘+’ is on rational is commutative]
(iii) a * b = a + ab
b * a = b + ab
Clearly, a + ab ¹ b + ab
So, * is not commutative.
(iv) a * b = (a – b)² , ∀ a , b ∈ Q
b * a = (b – a)²
∵ (a – b)² = (b – a)²
Hence, * is commutative.

Question. Using the definition, prove that the function f : A→ B is invertible if and only if f is both one-one and onto.
Answer. A function f : X → Y is defined to be invertible, if there exist a function g = Y → X such that gof = I_x and fog = I_y . The function is called the inverse of f and is denoted by f^-1. A function f = X → Y is invertible iff f is a bijective function

Question. Each of the following defines a relation of N
(i) x is greater than y, x, y ∈ N.
(ii) x + y = 10, x, y ∈ N.
(iii) xy is square of an integer x, y ∈ N.
(iv) x + 4y = 10, x, y ∈ N
Determine which of the above relations are reflexive, symmetric and transitive.
Answer. (i) x is greater than y, x, y ∈N
(x, x)∈R
For xRx x > x is not true for any x ∈ N.
Therefore, R is not reflexive.
Let (x, y)∈ R                                       ⇒ xRy
                                               x > y
but y > x is not true for any x, y ∈ N
Thus, R is not symmetric.
Let xRy and yRz
x > y and y > z                               ⇒ x > z
                                                      ⇒ xRz
So, R is transitive.

Question. Give an example of a map
(i) which is one-one but not onto.
(ii) which is not one-one but onto.
(iii) which is neither one-one nor onto.
Answer. (i) Let f : N → N, be a mapping defined by f(x) = 2x which is one-one.

Question. Let R be relation defined on the set of natural number N as follows, R = {(x, y) : x ∈ N, y ∈ N, 2x + y = 41}. Find the domain and range of the relation R. Also verify whether R is reflexive, symmetric and transitive.
Answer Given that, R = {(x, y) : x ∈ N, y ∈ N, 2x + y = 41}.
Domain = {1, 2, 3,,,,,,,,,,,,,,,,,,,,,,,,,, 20}
Range = {1, 3, 5, 7,,,,,,,,,,,,,,,,,,,,,, 39}
R = {(1, 39), (2, 37), (3, 35),…….., (19, 3), (20, 1)}
R is not reflexive as (2, 2) ∈ R
2 x 2 + 2 ≠ 41
So, R is not symmetric.
As (1, 39) ∈ R but (39, 1) ∈ R
So, R is not transitive.
As (11, 19) ∈ R, (19, 3) ∈ R
But (11, 3) ∈ R
Hence, R is neither reflexive, nor symmetric and nor transitive.

Question. If A = {1, 2, 3,4}, define relations on A which have properties of being
(i) reflexive, transitive but not symmetric.
(ii) symmetric but neither reflexive nor transitive.
(iii) reflexive, symmetric and transitive.
Answer. Given that, A = {1, 2, 3, 4}
(i) Let R₁ = {(1, 1), (1, 2), (2, 3), (2, 2), (1, 3), (3, 3)}
R₁ is reflexive, since, (1, 1) (2, 2) (3, 3) lie in R₁.
Now, (1, 2) 1 ∈ R , (2, 3) 1 ∈ R ⇒ (1, 3) ∀ 1 ∈ R
Hence, R₁ is also transitive but (1, 2) 1 ∈ R ⇒ (2, 1) 1 ∈ R .
So, it is not symmetric.
(ii) Let R₂ = {(1, 2), (2, 1)}
Now, (1, 2) 2 ∈ R , (2, 1) 2 ∈ R
So, it is symmetric.
(iii) Let R₃ = {(1, 2), (2, 1), (1, 1), (2, 2), (3, 3), (1, 3), (3, 1), (2, 3)}
Hence, R₃ is reflexive, symmetric and transitive.