MCQs for Mathematics Class 12 with Answers Chapter 13 Probability
Students of class 12 Mathematics should refer to MCQ Questions Class 12 Mathematics Probability with answers provided here which is an important chapter in Class 12 Mathematics NCERT textbook. These MCQ for Class 12 Mathematics with Answers have been prepared based on the latest CBSE and NCERT syllabus and examination guidelines for Class 12 Mathematics. The following MCQs can help you to practice and get better marks in the upcoming class 12 Mathematics examination
Chapter 13 Probability MCQ with Answers Class 12 Mathematics
MCQ Questions Class 12 Mathematics Probability provided below have been prepared by expert teachers of grade 12. These objective questions with solutions are expected to come in the upcoming Standard 12 examinations. Learn the below provided MCQ questions to get better marks in examinations.
Question. A bag contains 3 white, 4 black and 2 red balls. If 2 balls are drawn at random (without replacement), then the probability that both the balls are white is
(a) 1/18
(b) 1/36
(c) 1/12
(d) 1/24
Answer
C
Question. Two dice are thrown. If it is known that the sum of number on the dice was less than 6, the probability of getting a sum 3, is
(a) 1/18
(b) 5/18
(c) 1/5
(d) 2/5
Answer
C
Question. Which one of the following is not a requirement of a binomial distribution?
(a) There are two outcomes for each trial
(b) There is a fixed number of trials
(c) The outcomes must be dependent on each other.
(d) The probability of success must be the same for all trials.
Answer
C
Question. A and B are events such that P(A) = 0.4, P(B) = 0.3 and P(A , B) = 0 .5. Then P(B’ + A) equals
(a) 2/3
(b) 1/2
(c) 3/10
(d) 1/5
Answer
D
Question. Let X be a discrete random variable assuming values x1, x2, …, xn with probabilities p1, p2, …, pn, respectively. Then variance of X is given by
(a) E(X2)
(b) E(X2) + E(X)
(c) E(X2) – [E(X)]2
(d) √E(X2) – [E(X)]2
Answer
C
Question. Three persons, A, B and C, fire at a target in turn, starting with A. Their probability of hitting the target are 0.4, 0.3 and 0.2 respectively. The probability of two hits is
(a) 0.024
(b) 0.188
(c) 0.336
(d) 0.452
Answer
B
Question. Assume that in a family, each child is equally likely to be a boy or a girl. A family with three children is chosen at random. The probability that the eldest child is a girl given that the family has at least one girl is
(a) 1/2
(b) 1/3
(c) 2/3
(d) 4/7
Answer
D
Question. From the set {1, 2, 3, 4, 5}, two numbers a and b ( a ! b ) are chosen at random. The probability that a/b is an integer is
(a) 1/3
(b) 1/4
(c) 1/2
(d) 3/5
Answer
B
Question. A box contains 3 orange balls, 3 green balls and 2 blue balls. Three balls are drawn at random from the box without replacement. The probability of drawing 2 green balls and one blue ball is
(a) 3/28
(b) 2/21
(c) 1/28
(d) 167/168
Answer
A
Question. A flashlight has 8 batteries out of which 3 are dead. If two batteries are selected without replacement and tested, the probability that both are dead is
(a) 33/56
(b) 9/64
(c) 1/14
(d) 3/28
Answer
D
Question. A bag contains 5 red and 3 blue balls. If 3 balls are drawn at random without replacement, then the probability of getting exactly one red ball is
(a) 15/196
(b) 131/392
(c) 15/56
(d) 15/29
Answer
C
Question. Three persons A, B and C, fire at a target in turn, standing with A. Their probability of hitting the target are 0.4, 0.3 and 0.2 respectively. The probability of two hits is
(a) 0.025
(b) 0.188
(c) 0.339
(d) 0.475
Answer
B
Question. You are given that A and B are two events such that P(B) =3/5 ,P(A | B) = 1/2 and P(A∪B) =4/5, then P(A) equals
(a) 3/10
(b) 1/5
(c) 1/2
(d) 3/5
Answer
C
Question. The probability distribution of a discrete random variable X is given below:

The value of k is
(a) 8
(b) 16
(c) 32
(d) 48
Answer
C
Question. Two dice are thrown together. Let A be the event ‘getting 6 on the first die’ and B be the event ‘getting 2 on the second die’, then P(A∩B) is
(a) 1/36
(b) 7/4
(c) 9/20
(d) None of these
Answer
A
Question. In a college, 30% students fail in Physics, 25% fail in Mathematics and 10% fail in both. One student is chosen at random. The probability that she fails in Physics if she has failed in Mathematics is
(a) 1/10
(b) 2/5
(c) 9/20
(d) 1/3
Answer
Question. Two cards are drawn from a well shuffled deck of 52 playing cards with replacement. The probability, that both cards are queens, is
(a) 1/13 x 1/13
(b) 1/13 x 1/12
(c) 1/13 x 1/17
(d) 1/13 x 4/51
Answer
A
Question. A and B are two students. Their chances of solving a problem correctly are 1/3 and 1/4 respectively. If the probability of their making a common error is, 1/20 and they obtain the same answer, then the probability of their answer to be correct is
(a) 1/12
(b) 1/40
(c) 13/120
(d) 10/13
Answer
D
Question. A die is thrown and a card is selected at random from a deck of 52 playing cards. The probability of getting an even number on the die and a spade card is
(a) 1/2
(b) 1/4
(c) 1/8
(d) 3/4
Answer
C
Question. A multiple choice examination has 5 questions. Each question has three alternative answers of which exactly one is correct. The probability that a student will get 4 or more correct answers just by guessing is
(a) 17/35
(b) 13/35
(c) 11/35
(d) 10/35
Answer
C
Question. Three numbers are chosen at random without replacement from {1, 2, 3,…,8}. The probability that their minimum is 3, given that their maximum is 6,is
(a) 3/8
(b) 1/5
(c) 1/4
(d) 2/5
Answer
B
Question. One ticket is selected at random from 50 tickets numbered 00, 01, 02, …, 49. Then, the probability that the sum of the digits on the selected ticket is 8, given that the product of these digits is zero, equals to
(a) 1/14
(b) 1/7
(c) 5/14
(d) 1/50
Answer
A
Question. Consider 5 independent Bernoulli’s trials each with probability of success p. If the probability of at least one failure is greater than or equal to 31/32, then p lies in the interval

Answer
B
Question. In a binomial distribution B (n, p =1/4), if the probability of atleast one success is greater than or equal to 9/10

Answer
A
The probability of happening of an event in one trial being known, then the probability of its happening exactly x times in n trials is given by n Cx q n-x. Px where
p = probability of happening the event
q = probability of not happening the event = 1− p
Now, nCx qn-x Px is (x +1) th term in the expansion of (q +P)n
whose expansion gives the happening of the event 0, 1, 2, …, n times, respectively.
Question. A man takes a forward step with probability (.8) and backward step with probability (.2). What is the probability that at the end of 9 steps he is exactly three steps away from starting point.
(a) 69888/58
(b) 5377/58
(c) 5378/58
(d) 5376/58
Answer
A
Question. Unbiased coin is tossed 6 times. The probability of getting at most 4 heads is
(a) 7/64
(b) 57/64
(c) 21/32
(d) 11/32
Answer
B
Question. In four throws with a pair of dice, the chance of throwing doublets at least twice is
(a) 19/144
(b) 125/144
(c) 17/144
(d) 18/144
Answer
A
Assertion and Reason
Each of these questions contains two statements : Statement I (Assertion) and Statement II (Reason). Each of these questions also has four alternative choices, only one of which is the correct answer. You have to select one of the codes (a), (b), (c) and (d) given below.
(a) Statement I is true, Statement II is true; Statement II is a correct explanation for Statement I.
(b) Statement I is true, Statement II is true; Statement II is not a correct explanation for Statement I.
(c) Statement I is true; Statement II is false.
(d) Statement I is false; Statement II is true.
Question. Consider the system of equations ax by + = 0, cx+ dy = 0, where a, b, c, d ∈{0 ,1 }
Statement I The probability that the system of equations has a unique solution 3/8 and
Statement II The probability that the system of equations has a solution is 1.
Answer
B
Question. Let A and B are two events such that P (A) =3/5 and P B=2/3, then
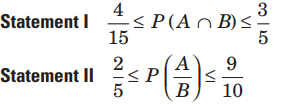
Answer
A
Question. Consider a natural number x is chosen at random from the first 100 natural numbers.

Answer
B
Question. Consider the relation

Statement I 20 persons are sitting in a row. These persons are selected at random. The probability that two selected persons are not together is 0.7.
Statement II If A is an event, then P(not A)=1-P(A)
Answer
D
Question. Statement I If 12 coins are thrown simultaneously, then probability of appearing exactly five head is equal to probability of appearing exactly 7 heads.
Statement II n Cr= n Cs ⇒either r =s or r +s =n and P(H) = P(T) in a single trial.
Answer
A

We hope the above multiple choice questions for Class 12 Mathematics for Chapter 13 Probability provided above with answers based on the latest syllabus and examination guidelines issued by CBSE, NCERT and KVS are really useful for you. Probability is an important chapter in Class 12 as it provides very strong understanding about this topic. Students should go through the answers provided for the MCQs after they have themselves solved the questions. All MCQs have been provided with four options for the students to solve. These questions are really useful for benefit of class 12 students. Please go through these and let us know if you have any feedback in the comments section.
