MCQs for Mathematics Class 12 with Answers Chapter 6 Application of Derivatives
Students of class 12 Mathematics should refer to MCQ Questions Class 12 Mathematics Application of Derivatives with answers provided here which is an important chapter in Class 12 Mathematics NCERT textbook. These MCQ for Class 12 Mathematics with Answers have been prepared based on the latest CBSE and NCERT syllabus and examination guidelines for Class 12 Mathematics. The following MCQs can help you to practice and get better marks in the upcoming class 12 Mathematics examination
Chapter 6 Application of Derivatives MCQ with Answers Class 12 Mathematics
MCQ Questions Class 12 Mathematics Application of Derivatives provided below have been prepared by expert teachers of grade 12. These objective questions with solutions are expected to come in the upcoming Standard 12 examinations. Learn the below provided MCQ questions to get better marks in examinations.
Question. y = x (x – 3)2 decreases for the values of x given by
(a) 1 < x < 3
(b) x < 0
(c) x > 0
(d) 0 < x < 3/2
Answer
A
Question. The function f (x) = x +cos x is
(a) always increasing
(b) always decreasing
(c) increasing for certain range of x
(d) None of the above
Answer
A
Question. The tangent at (1,7) to the curve x2 =y- 6 touches the circle x2 +y2 +16x+12y + c=0 at
(a) (6,7 )
(b) -6,7 ) −6 7
(c) (6,-7)
(d) (-6,-7)
Answer
D
Question. The function f (x) =x(x+3)e-(1/2)x satisfies all the conditions of Rolle’s theorem in [-3,0]. The value of c is
(a) 0
(b) −1
(c) −2
(d) −3
Answer
C
Question. Let f (x) satisfy all the conditions of mean value theorem in [0 ,2 ]. If f(0)= 0 = and|f’ (x)| ≤ 1/2 for all x, in [0,2] then
(a) f(x) < 2
(b) |f(x)| ≤ 1
(c) f (x)=2x
(d) f (x ) = 3 for at least one x in [0 ,2]
Answer
B
Question. The function f (x)= x3-6×2+ ax + b satisfy the conditions of Rolle’s theorem in [ 1,3 ]. The values of a and b are
(a) 11, 6
(b) −6, 11
(c) −11, 6
(d) 6-, 11
Answer
A
Question. The function f(x)= x-3)2 satisfies all the conditions of mean value theorem in[3, 4]. A point on y= (x-3)2, where the tangent is parallel to the chord joining (3, 0) and (4,1) is
(a) (7/2,1/2)
(b) (7/2,1/4)
(c) (1,4 )
(d) (4 ,1)
Answer
B
Question. The function f (x)= cos x − 2px is monotonically decreasing for
(a) p <1/2
(b) p >1/2
(c) p < 2
(d) p > 2
Answer
B
Question. Let a b + = 4, a < 2 and g (x ) be a monotonically increasing function of x. Then,

(a) increases with increase in (b-a )
(b) decreases with increase in (b-a)
(c) increases with decreases in (b-a)
(d) None of the above
Answer
A
Question. In the mean value theorem, f(b)-f(a)=(b-a)f’ (c), if a =4,b=9 and f(x)=√x, then the value of c is
(a) 8.00
(b) 5.25
(c) 4.00
(d) 6.25
Answer
D
Question. The function which is neither decreasing nor increasing in [π/2,3π/2]
(a) cosec x
(b) tan x
(c) x2
(d) |x − 1|
Answer
A
Question. The values of a in order that f(x)=√3 sin x -cos x-2ax+b decreases for all real values of x, is given by
(a) a < 1
(b) a ≥ 1
(c) a ≤ √2
(d) a < √2
Answer
B
Question. The abscissa of the points of the curve y= x3 in the interval [−2, 2], where the slope of the tangents can be obtained by mean value theorem for the interval
[−2, 2], are
(a) ±2/√3
(b) + √3
(c) ±√3/2
(d) 0
Answer
A
Question. The sum of intercepts on coordinate axes made by tangent to the curve √x+√y =√a is
(a) a
(b) 2a
(c) 2√a
(d) None of these
Answer
A
Question. The equation of the tangent to the curve y=1- ex/2 at the point of intersection with the y-axis is
(a) x+ 2y + = 2 0
(b) 2x+y=0
(c) x- y = 2
(d) None of these
Answer
A
Question. The total number of parallel tangents of f1 (x) =x2-x+1 and f2(x) = x3-x2-2x+1 are
(a) 2
(b) 0
(c) 1
(d) infinite
Answer
D
Question. The chord joining the points, where x p = and x q = on the curve y= ax2+ bx +c is parallel to the tangent at the point on the curve whose abscissa is
(a) p+ q /2
(b) p- q /2
(c) p q/2
(d) None of these
Answer
A
Question. In [0, 1], Lagrange’s mean value theorem is not applicable to

Answer
D
Question.
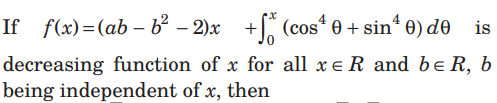
(a) a ∈( 0,√6)
(b) a ∈ (- √6,√6 )
(c) a ∈ (-√6,0)
(d) None of these
Answer
B
Question.
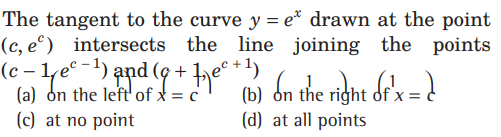
Answer
A
Question. For the curve y = 4x3-2x5, the points at which the tangent passes through the origin are
(a) (0, 0), (1,2) and (-1,-2)
(b) (0,0), (2 ,4) and (-1,-3)
(c) (0 ,0), (2,3 ) and (-3,-1)
(d) None of the above
Answer
A
Question. The approximate value of f( 5.001), where
f(x)=x3-7x2+15,i(a) − 34.995
(b) − 33.995
(c) − 33.335
(d) − 35.993
Answer
A
Question. The length of sub tangent to the curve x2 y2=a4 at the point (-a ,a) is
(a) 3 a
(b) 2 a
(c) a
(d) 4a
Answer
C
Question. The point at which the tangent to the curve y= 2x2-x+1 is parallel to y = 3x+9, will be
(a) (2, 1)
(b) (1, 2)
(c) (3, 9)
(d) (-2,1)
Answer
B
Question. For the curve x y = c2, the subnormal at any point varies
(a) x2
(b) x3
(c) y2
(d) y3
Answer
D
Question. The abscissa of the points, where the tangent to the curve y=x3-3×2-9x+5 is parallel to x-axis, are
(a) x = 0 and 0
(b) x = 1and −1
(c) x = 1and −3
(d) x = −1and 3
Answer
D
Question. If tangent to the curve x = at2, y=2at is perpendicular to x-axis, then its point of contact is
(a) (a ,a)
(b) (0,a )
(c) (0, 0)
(d) (a ,0)
Answer
C
Question. The slope of the tangent to the curve x=3t2 + 1,y = t3-1, at x =1 is
(a) 0
(b) 1/2
(c) ∞
(d) −2
Answer
A
Question. The point on the curve √x +√y =√a at which the normal is parallel to the x-axis, is
(a) (0,0)
(b) (0,a)
(c) (a,0)
(d) (a, a)
Answer
B
Question. The equation of the tangent to the curve (1+ x2) y=2-x,where it crosses the x-axis, is
(a) x+ 5y=2
(b) x-5y=2
(c) 5x-y=2
(d) 5x +2 y-2=0
Answer
A
Question. Coordinates of a point on the curve y = x log at are
(a) (0, 0)
(b) (e ,e )
(c) (e2,2e2)
(d) (e-2,-2e-2)
Answer
D
Question. The tangent drawn at the point (0,1) on the curve y= e2x , meets x-axis at the point
(a) (1/2,0)
(b) (−1/2,0)
(c) (2, 0)
(d) (0, 0)
Answer
B
Question. The length of the normal at point ‘t’ of the curve x=a (t+ sin t), y=a(1-cost) is
(a) a sin t
(b) 2a sin3(t/2) sec(t/2)
(c) 2a sin (t/2) tan (t/2)
(d) 2a sin (t/2)
Answer
C
Question. The tangent to the curve y= 2×2-x+1 at a point P is parallel to y =x3+ 4, then the coordinates of Pare
(a) (2, 1)
(b) (1, 2)
(c) (-1,2)
(d) (2,-1)
Answer
B
Question. Tangent of the angle at which the curves y= ax= and

Answer
B
Question. The product of the lengths of sub tangent and subnormal at any point of a curve is
(a) square of the abscissa
(b) square of the ordinate
(c) constant
(d) None of these
Answer
B
Question. If the normal to the curve y =f (x) at the point (3,4) makes an angle 3π/2 with the positive x-axis, then f ′(3) is equal to
(a) −1
(b) −3/3
(c) 4/3
(d) 1
Answer
D
Question. The curve y- e xy + x=0 has a vertical tangent at the point
(a) (1, 0)
(b) at no point
(c) (0,1)
(d) (0, 0)
Answer
A
Question. The equation of tangent to the curve y=be-x/a the point where it crosses y-axis, is
(a) ax+ by + = 1
(b) ax- by − = 1
(c) x/a-y/b=1
(d) x/a +y/b=1
Answer
D
Question. The abscissa of the point on the curve 3y = 6x – 5x3, the normal at which passes through origin is
(a) 1
(b) 1/3
(c) 2
(d) 1/2
Answer
A
Question. A ladder, 5 meter long, standing on a horizontal floor, leans against a vertical wall. If the top of the ladder slides downwards at the rate of 10 cm/sec, then the rate at which the angle between the floor and the ladder is decreasing when lower end of ladder is 2 metres from the wall is
(a) 1/10 radian/sec
(b)1/20 radian/sec
(c) 20 radian/sec
(d) 10 radian/sec
Answer
B
Question. The curve y = x1/5 has at (0, 0)
(a) a vertical tangent (parallel to y-axis)
(b) a horizontal tangent (parallel to x-axis)
(c) an oblique tangent
(d) no tangent
Answer
A
Question. The rate of change of the area of a circle with respect to its radius r at r = 6 cm is
(a) 10p
(b) 12p
(c) 8p
(d) 11p
Answer
B
Question. f(x) = xx has a stationary point at
(a) x = e
(b) x=1/ e
(c) x = 1
(d) x = e
Answer
B
Question. The total revenue in rupees received from the sale of x units of a product is given by R(x) = 3x2 + 36x + 5. The marginal revenue, when x = 15 is
(a) 116
(b) 96
(c) 90
(d) 126
Answer
D
Question. The maximum value of (1/x)x is
(a) e
(b) ee
(c) e1/e
(d) (1/e)1/e
Answer
C
Question. The two curves x3 – 3xy2 + 2 = 0 and 3x2y – y3 = 2 [NCERT Exemplar]
(a) touch each other
(b) cut at right angle
(c) cut at an angle π/3
(d) cut at an angle π/4
Answer
B
Question. The equation of normal to the curve 3x2 – y2 = 8 which is parallel to the line x + 3y = 8 is
(a) 3x – y = 8
(b) 3x + y + 8 = 0
(c) x + 3y ± 8 =0
(d) x + 3y = 0
Answer
C
Question. The tangent to the curve given by x = et.cos t, y = et. sint at t = π/4 makes with x-axis an angle
(a) 0
(b) π/4
(c) π/3
(d) π/2
Answer
D
Question. The interval in which the function f given by f(x) = x2 e–x is strictly increasing, is
(a) (– ∞, ∞)
(b) (– ∞, 0)
(c) (2, ∞)
(d) (0, 2)
Answer
D
Question. The slope of normal to the curve y = 2x2 + 3 sin x at x = 0 is
(a) 3
(b) 1/3
(c) –3
(d) 1/3
Answer
D
Question. The equation of the normal to the curve y = sinx at (0, 0) is
(a) x = 0
(b) y = 0
(c) x + y = 0
(d) x – y = 0
Answer
C
Question. The point on the curve y2 = x, where the tangent makes an angle of π/4 with x-axis is
(a) (1/2 , 1/4)
(b) (1/2 , 1/4)
(c) (4, 2)
(d) (1, 1)
Answer
B
Question. The tangent to the curve y = e2x at the point (0, 1) meets x-axis at
(a) (0, 1)
(b) b(–1/2, 0l
(c) (2, 0)
(d) (0, 2)
Answer
B
Question. The point on the curve x2 = 2y which is nearest to the point (0, 5) is
(a) (2√2, 4)
(b) (2√2, 0)
(c) (0, 0)
(d) (2, 2)
Answer
A
Question. If x is real, the minimum value of x2 – 8x + 17 is [NCERT Exemplar]
(a) – 1
(b) 0
(c) 1
(d) 2
Answer
C
Question. The line y = x +1 is a tangent to the curve y2 = 4x at the point
(a) (1, 2)
(b) (2, 1)
(c) (1, – 2)
(d) (–1, 2)
Answer
A
Question. The points at which the tangents to the curve y = x3 – 12x + 18 are parallel to x-axis are
(a) (2, –2), (–2, –34)
(b) (2, 34), (–2, 0)
(c) (0, 34), (–2, 0)
(d) (2, 2), (–2, 34)
Answer
D
Question. The sides of an equilateral triangle are increasing at the rate of 2 cm/sec. The rate at which the area increases, when side is 10 cm is
(a) 10 cm2/s
(b) 3 cm2/s
(c) 10√3 cm2/s
(d) 10/3 cm2/s
Answer
C
Question. The maximum value of slope of the curve y = – x3 + 3x2 + 12x – 5 is [CBSE 2020 (65/3/1)]
(a) 15
(b) 12
(c) 9
(d) 0
Answer
A
Question. If the function f(x) = 2x2 – kx + 5 is increasing on [1, 2], then k lies in the interval
(a) (– ∞, 4)
(b) (4, ∞)
(c) (– ∞, 8)
(d) (8, ∞)
Answer
A
Question. If the curve ay + x2 = 7 and x3 = y, cut orthogonally at (1, 1), then the value of a is
(a) 1
(b) 0
(c) – 6
(d) 6
Answer
D
Question. The approximate value of (33)1/5is
(a) 2.0125
(b) 2.1
(c) 2.01
(d) none of these
Answer
A
Question. The equation of the normal to the curve y = x (2 – x) at the point (2, 0) is
(a) x – 2y = 2
(b) x – 2y + 2 = 0
(c) 2x + y = 4
(d) 2x + y – 4 = 0
Answer
A
Question. The angle of intersection of the parabolas y2 = 4ax and x2 = 4ay at the origin, is
(a) π/6
(b) π/3
(c) π/2
(d) π/4
Answer
C
Question. The slope of the tangent to the curve y = x3 – x at the point (2, 6) is _____________ .
Answer
11
Question. The maximum value of f (x)=x+1/x , x< 0 is _____________ .
Answer
2
Question. The rate of change of the area of a circle with respect to its radius r, when r = 3 cm, is_____________ .
Answer
6πcm2/cm
Question. If f (x) = 1/4x2+ 2x+ 1 , then its maximum value is _____________ .
Answer
4/3

We hope the above multiple choice questions for Class 12 Mathematics for Chapter 6 Application of Derivatives provided above with answers based on the latest syllabus and examination guidelines issued by CBSE, NCERT and KVS are really useful for you. Application of Derivatives is an important chapter in Class 12 as it provides very strong understanding about this topic. Students should go through the answers provided for the MCQs after they have themselves solved the questions. All MCQs have been provided with four options for the students to solve. These questions are really useful for benefit of class 12 students. Please go through these and let us know if you have any feedback in the comments section.
