MCQs for Mathematics Class 12 with Answers Chapter 8 Application of Integrals
Students of class 12 Mathematics should refer to MCQ Questions Class 12 Mathematics Application of Integrals with answers provided here which is an important chapter in Class 12 Mathematics NCERT textbook. These MCQ for Class 12 Mathematics with Answers have been prepared based on the latest CBSE and NCERT syllabus and examination guidelines for Class 12 Mathematics. The following MCQs can help you to practice and get better marks in the upcoming class 12 Mathematics examination
Chapter 8 Application of Integrals MCQ with Answers Class 12 Mathematics
MCQ Questions Class 12 Mathematics Application of Integrals provided below have been prepared by expert teachers of grade 12. These objective questions with solutions are expected to come in the upcoming Standard 12 examinations. Learn the below provided MCQ questions to get better marks in examinations.
Question. The area of the region bounded by the y-axis, y = cos x and y = sin x, 0≤x≤ π/2 is
(a) √2 sq units
(b) (√2 + 1) sq units
(c) (√2 – 1) sq unit
(d) (2√2 – 1) sq units
Answer
C
Question. The area between x =y2 and x = 4 is divided into two equal parts by the line x a = , the value of a is
(a) (2 )2/3
(b) √2
(c) (4)4/3
(d) (4 )2/3
Answer
D
Question. The area of the region bounded by the curve y2=4x and the line x = 3 is
(a) 2 √3 sq units
(b) 8 √3 sq units
(c) 4 √3 sq units
(d) 3 √3 sq units
Answer
B
Question. The area of the region bounded by y2=9x, x=2,x=4 and the X-axis in the first quadrant is
(a) 16 sq units
(b) 4 √2 sq units
(c) 4 (4- √2 sq units
(d) 4 (4+ √2) + sq units
Answer
C
Question. Sketch the graph of y = + |x+3 |and the value of

(a) 9 sq units
(b) 9/2 sq units
(c) 3 sq units
(d) 11 sq units
Answer
A
Question. The area bounded by the curve y = x| x|, -axis and the coordinates x = -1 and x = 1 is given by
(a) 0
(b) 1/3
(c) 2/3
(d) 4/3
Answer
C
Question. Area lying in the first quadrant and bounded by the circle x2 +y2=4 and the lines x = 0 and x = 2 is
(a) π units
(b) π/2 units
(c) π/3 units
(d) π/4 units
Answer
A
Question. Draw a rough sketch of the curve y= √x-1 in the interval[1,5]. The area under the curve and between the lines x = 1 and x = 5 is
(a) 4/3 sq units
(b) 8/3 sq units
(c) 16/3 sq units
(d) None of these
Answer
C
Question. The area of the region bounded by the curve ay2 =x3,the Y-axis and the lines y = a and y= 2a is

Answer
A
Question. Using integration, the area of the region bounded by the line 2y= 5x+ 7, x axis and the lines x = 2 and x = 8 is
(a) 96 sq units
(b) 72 sq units
(c) 84 sq units
(d) None of these
Answer
A
Question. The area of the region bounded by the curve xy- 3x- 2y -10=0, X-axis and the lines x=3,x=4
(a) 3 sq units
(b) 3 + 16 log 2 sq units
(c) 16 log 2 sq units
(d) None of these
Answer
B
Question. The area bounded by the curve x=2- y-y2 and Y-axis is
(a) 3/2 sq units
(b) 5/2 sq units
(c) 9/2 sq units
(d) None of these
Answer
C
Question. The area bounded by the curve |x| +y = 1 and axis of x is
(a) 1 sq unit
(b) 2 sq units
(c) 8 sq units
(d) None of these
Answer
A
Question. The area bounded by the curves f (x)= cex(c>0), the X-axis and the two ordinates x= p = and x= q = , is proportional to
(a) f (p) f(q)
(b) |f (p)- f(q)|
(c) f (p) +f(q)
(d) √f(p f(q)
Answer
B
Question. The area bounded by x=1, x=2, xy =1 and X-axis is
(a) (log )2 sq unit
(b) 2 sq units
(c) 1 sq unit
(d) None of these
Answer
A
Question. The area included between the curves y=1/x2+1 and X-axis is
(a)π/2 sq units
(b) π sq units
(c) 2π sq units
(d) None of these
Answer
B
Question. The area between the curve y=4+3x-x2 and X-axis is
(a) 125/6 sq units
(b) 125/3 sq units
(c) 125/2 sq units
(d) None of these
Answer
A
Question. If the area above X-axis, bounded by the curves y=2 kx and x = 0 and x = 2 is 3/log2, then the value of k is
(a) 1/2
(b) 1
(c) -1
(d) 2
Answer
B
Question. The area bounded by y =tan-1 x, x=1 and X- axis is
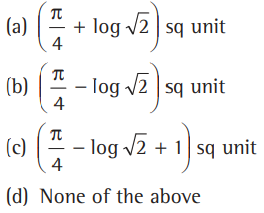
Answer
B
Question. Area enclosed between the curve y2(2a-x)= x3 and line x= 2a above X-axis is
(a)πa2 sq units
(b) 3πa2/2 sq units
(c) p πa2 sq units
(d) 32a2 sq units
Answer
B
Question. The area bounded by the curve y = sin2 x and lines x= π/2,x= π and X-axis is
(a) π/2 sq unit
(b) π/4 sq unit
(c) π/8 sq unit
(d) None of these
Answer
B
Question. The area bounded by the curve y x y = = sec2 x, y=0 0 and |x| =p/3 is
(a) √3 sq units
(b) √2 sq units
(c) 2 √3 sq units
(d) None of these
Answer
C
Question. The area bounded by y= sin-1 x, x=1/√2 and X-axis is

Answer
D
Question. The area bounded by y= e -x, X- axis and x≥ 0 is
(a) 1
(b) 2
(c) 1/e
(d) e
Answer
A
Question. The area bounded by the curve y = f(x)loge x, the X-axis and the straight line x = e is
(a)1- 1/e sq unit
(b) 1 sq unit
(c) 1-1/e sq unit
(d) 1+1/e sq unit
Answer
B
Question. The area of the smaller part of the circle x2 +y2=a2 cut-off by the line x=a/√2 is

Answer
B
Question. The area bounded by y =x3-4x and X-axis is
(a) 5
(b) 9
(c) 8
(d) 12
Answer
C
Question. Area of the region in the first quadrant enclosed by the x-axis, the line y = x and the circle x2 + y2 = 32 is
(a) 16π sq units
(b) 4π sq units
(c) 32π sq units
(d) 24 sq units
Answer
B
Question. The area of the region bounded by the line y – 1 = x, the x-axis and the ordinates x = – 2 and x = 3 is
(a) 4/3 sq units
(b) 7/2 sq units
(c) 17/2 sq units
(d) 16/3 sq units
Answer
C
Question. Area of the region bounded by the curve y = cos x between x = 0 and x = π is
(a) 2 sq units
(b) 4 sq units
(c) 3 sq units
(d) 1 sq unit
Answer
A
Question. The area of the circle x2 + y2 = 16 exterior to the parabola y2 = 6x is
(a) 4/3 (4π – √3h sq. units
(b) 4/3 (4π + √3h sq. units
(c) 4/3 (8π – √3h sq. units
(d) 4/3 (8π + √3h sq. units
Answer
C
Question. The area of the region bounded by the curve x = 2y + 3 and the lines y = 1 and y = –1 is
(a) 4 sq units
(b) 3/2 sq units
(c) 6 sq units
(d) 8 sq units
Answer
C
Question. The area of the region bounded by the parabola y2 = x and the straight line 2y = x is
(a) 4/3 sq. units
(b) 1 sq. unit
(c) 2/3 sq. unit
(d) 1/3 sq. unit
Answer
A
Question. The area of the curve y = sin x between 0 and π is
(a) 2 sq units
(b) 4 sq units
(c) 12 sq units
(d) 14 sq units
Answer
A
Question. The area enclosed by the circle x2 + y2 = 2 is equal to
(a) 4π sq units
(b) 2 2r sq units
(c) 4π2 sq units
(d) 2π sq units
Answer
D
Question. The area of the region bounded by the curve ay2 = x3, the y-axis and the lines y = a and y = 2a is
(a) 3 sq units
(b) 3/5 a2 |2X22/3–1 | sq units
(c) 3/5 a |22/3–1 | sq units
(d) 1 sq unit
Answer
B
Question. The area bounded by the curve y = |sin x|, x-axis and ordinates x = p and x = 10p is equal to
(a) 8 sq. units
(b) 10 sq. units
(c) 18 sq. units
(d) 20 sq. units
Answer
C
Question. The area enclosed by the curve x = 3 cos t, y = 2 sin t is
(a) 4π sq units
(b) 6π sq units
(c) 14π sq units
(d) 7π sq units
Answer
B
Question. The area bounded by the curve y = x |x|, x-axis and the ordinates x = – 1 and x = 1 is given by
(a) 0 sq. units
(b) 1/3 sq. unit
(c) 2/3 sq. unit
(d) 4/3 sq. units
Answer
C
Question. The area enclosed by the ellipse x2/a2 + y2/b2 =1+ = is equal to
(a) π2 ab sq units
(b) π ab sq units
(c) πa2 b sq units
(d) π ab2 sq units
Answer
Question. Area lying in the first quadrant and bounded by the circle x2 + y2 = 4 and the line x = 0 and x = 2 is
(a) r sq. units
(b) π/2 sq. units
(c) π/3 sq. units
(d) π/4 sq. units
Answer
A
Question. The area of the region bounded by the curve y = x2 and the line y = 16 is
(a) 37/3sq units
(b) 256/3 sq units
(c) 64/3sq units
(d) 128/3sq units
Answer
B
Question. The area of the region bounded by the curve x2 = 4y and the straight line x = 4y – 2 is
(a) 3/8 sq unit
(b) 5/8 sq unit
(c) 7/8 sq unit
(d) 9/8 sq units
Answer
D
Question. The area of the region bounded by the curves x = at2 and y = 2at between the ordinate corresponding to t = 1 and t = 2 is
(a) 56/3 a2 sq units
(b) 40/3 a2 sq units
(c) 5π sq units
(d) None of these
Answer
A
Question. The area of a minor segment of the circle x2 + y2 = a2 cut off by the line x = a/2 is
(a) a2/12(4π -3√3) sq units
(b) a2/4(4π -3√3) sq units
(c) a2/12(3π -4) sq units
(d) None of these
Answer
A
Question. The area of the region bounded by the curve y = x3 and y = x + 6 and x = 0 is
(a) 7 sq units
(b) 6 sq units
(c) 10 sq units
(d) 14 sq units
Answer
C
Question. The area under the curve y = 2√x included between the lines x = 0 and x = 1 is
(a) 4 sq units
(b) 3 sq units
(c) 4/3 sq units
(d) None of these
Answer
C
Question. The area under the curve y = √(a2 – x2) included between the lines x = 0 and x = a is
(a) πa2/4 sq units
(b) a2/4 sq units
(c) πa2 sq units
(d) 4π sq units
Answer
A
Question. The area of the region bounded by the curve y = √(16 – x2) and x-axis is
(a) 8 p sq units
(b) 20π sq units
(c) 16π sq units
(d) 256π sq units
Answer
A
Question. The area of the region bounded by the triangle whose vertices are (–1, 1), (0, 5) and (3, 2) is
(a) 15/2 sq units
(b) 15 sq units
(c) 4 sq units
(d) 10 sq units
Answer
A
Question. The area of the region bounded by the curve y2 = 9x, y = 3x is
(a) 1 sq unit
(b) 1/2sq unit
(c) 4 sq units
(d) 14 sq units
Answer
B
Question. The area of the region bounded by the curve x = y2, y-axis and the line y = 3 and y = 4 is ___________.
Answer
37/3 sq. units
Question. The area bounded by the curve y = sin x, x-axis and the ordinates x = 0 and x = p is ___________.
Answer
2 sq. units
Question. The area of the region bounded by the curve y = x – x2 between x = 0 and x = 1 is ___________. 1/6 sq. unit
Answer
Question. The area of the region bounded by the ellipse x2/25 + y2/16 =1 is ___________. 20p sq. units
Answer

We hope the above multiple choice questions for Class 12 Mathematics for Chapter 8 Application of Integrals provided above with answers based on the latest syllabus and examination guidelines issued by CBSE, NCERT and KVS are really useful for you. Application of Integrals is an important chapter in Class 12 as it provides very strong understanding about this topic. Students should go through the answers provided for the MCQs after they have themselves solved the questions. All MCQs have been provided with four options for the students to solve. These questions are really useful for benefit of class 12 students. Please go through these and let us know if you have any feedback in the comments section.
