Students of Class 9 Mathematics should refer to MCQ Questions Class 9 Mathematics Areas of Parallelogram and Triangle with answers provided here which is an important chapter in Class 9 Mathematics NCERT textbook. These MCQ for Class 9 Mathematics with Answers have been prepared based on the latest CBSE and NCERT syllabus and examination guidelines for Class 9 Mathematics. The following MCQs can help you to practice and get better marks in the upcoming Class 9 Mathematics examination

Chapter 9 Areas of Parallelogram and Triangle MCQ with Answers Class 9 Mathematics

MCQ Questions Class 9 Mathematics Areas of Parallelogram and Triangle provided below have been prepared by expert teachers of grade 9. These objective questions with solutions are expected to come in the upcoming Standard 9 examinations. Learn the below provided MCQ questions to get better marks in examinations.

Question. ABCD is a trapezium in which AB ∥ DC. A line through A parallel to BC meets diagonal BD at P. If ar(ΔBPC) = 5 cm², then ar (ΔABD) is

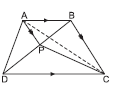
(a) 5 cm²
(b) 2.5 cm²
(c) 7.5 cm²
(d) 10 cm²

Question. PQRS is a trapezium with PQ ∥ SR. A line parallel to PR intersects PQ at X and QR at Y. If ar(ΔPYR) = 5 cm², then ar(ΔPXS) is

(a) 10 cm²
(b) 5 cm²
(c) 2.5 cm²
(d) 7.5 cm²

Question. Two parallelograms are on equal base and between the same parallels. The ratio of their areas is
(a) 1 : 2
(b) 2 : 1
(c) 1 : 1
(d) 3 : 1

Question. ABCD is a parallelogram. P is any point on CD. If ar(ΔDPA) = 15 cm² and ar (ΔAPC) = 20 cmm², then ar(ΔAPB) is
(a) 15 cm²
(b) 20 cm²
(c) 35 cm²
(d) 30 cm²

Question. In the given figure, PQRS is a rectangle. If PS = 8 cm and SR = 4 cm, then the area of ΔABC is

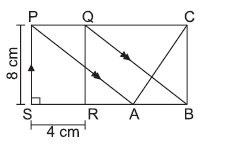
(a) 32 cm²
(b) 12 cm²
(c) 20 cm²
(d) 16 cm²

Question. PQRS is a parallelogram. A and B are any points on PQ and RQ respectively. If ar(ΔSBR) = 16 cm2 and ar(ΔPBQ) = 8 cm², then the area of ΔRAS is

(a) 8 cm²
(b) 16 cm²
(c) 24 cm²
(d) 32 cm²

Question. In the given figure, the area of quadrilateral ABCD is

(a) 24 cm²
(b) 13 cm²
(c) 21 cm²
(d) 42 cm²

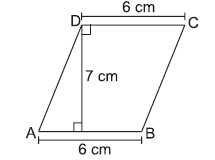
Question. ABCD is a parallelogram. If AB = 12 cm, AE = 7.5 cm, CF = 15 cm, then AD is equal to

(a) 6 cm
(b) 3 cm
(c) 10.5 cm
(d) 8 cm

Question. PQRS is a parallelogram and A and B are any points on PQ and QR respectively. If ar(∥gm PQRS) = 48 cm², then ar(ΔPBS) + ar(ΔASR) is equal to

(a) 24 cm²
(b) 96 cm²
(c) 36 cm²
(d) 48 cm²

Question. In the given figure, if ar(∥gm ABCD) = 29 cm² and AB = 5.8 cm, then the height of ∥gm ABEF is

(a) 4.8 cm
(b) 6 cm
(c) 5 cm
(d) 5.8 cm

Question. ABCD is a square. P and Q are mid-points of AB and DC respectively. If AB = 8 cm, then ar(ΔBPD) is

(a) 16 cm²
(b) 18 cm²
(c) 24 cm²
(d) 32 cm²

Question. ABC is a triangle in which D is the mid‑point of BC. E and F are mid‑points of DC and AE respectively. If ar (ΔABC) = 16 cm², then ar(ΔDEF) is

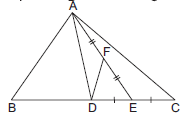
(a) 2 cm²
(b) 1 cm²
(c) 4 cm²
(d) 8 cm²

Question. ABCD and ABEF are parallelograms. M is any point of EB. If ar(∥gm ABCD) = 28 cm², then ar (ΔFAM) is

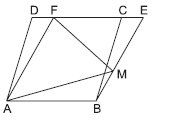
(a) 7 cm²
(b) 14 cm²
(c) 21 cm²
(d) 28 cm²

Question. The mid-point of the sides of a triangle along with any of the vertices as the fourth point make a parallelogram of area equal to
(a) ar(ΔABC)
(b) 1/2 ar(ΔABC)
(c) 1/3 ar(ΔABC)
(d) 1/4 ar(ΔABC)

Question. In quadrilateral PQRS, M is the mid-point of PR.If ar(quad SMQR) is 18 cm2, then ar (quad PQMS) is

(a) 24 cm²
(b) 18 cm²
(c) 12 cm²
(d) 36 cm²

Question. In the given figure, ABCD and AGEF are parallelograms. If ar(gm AGEF) = 27 cm², then ar(ΔADG) + ar(ΔGCB) is

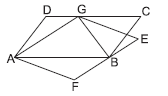
(a) 13.5 cm²
(b) 27 cm²
(c) 9 cm²
(d) 18 cm²

Question. In the given figure, ABCD is a parallelogram and its area is 64 cm2. If P is any point in the interior of ∥gm ABCD, then ar(ΔAPD) + ar(ΔPBC) is equal to

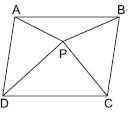
(a) 64 cm²
(b) 48 cm²
(c) 32 cm²
(d) 16 cm

Question. PQRS is a trapezium. A line drawn parallel to QP through R meets a line parallel to RP drawn through S at X. If ar(trap PQRS) is 22 cm² and ar (ΔPQR) = 8 cm², then ar(ΔPXR) is

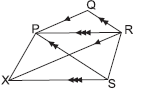
(a) 15 cm²
(b) 30 cm²
(c) 14 cm²
(d) 8 cm²

Question. D and E are mid-points of BC and AD respectively.If ar(ΔABC) = 10 cm², then ar (ΔEBC) is

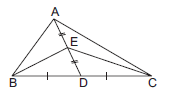
(a) 2.5 cm²
(b) 10 cm²
(c) 5 cm²
(d) 7.5 cm²

Question. ABCD is a trapezium with parallel sides AB = a cm and DC = b cm. E and F are the mid-points of the non-parallel sides. The ratio of ar(ABFE) to ar(EFCD) is

(a) a : b
(b) (a + 3b) : (3a + b)
(c) (3a + b) : (a + 3b)
(d) (2a + b) : (3a + b)

Question. Points A, B, C and D are collinear. AB = BC = CD.XY ∥ AD. If P and M lie on XY and ar(ΔMCD) = 7 cm², then ar(ΔAPB) and ar(ΔAPD) respectively are

(a) 7 cm² , 21 cm²
(b) 7 cm² , 14 cm²
(c) 14 cm² , 21 cm²
(d) 14 cm² , 14 cm²

Question. The median of a triangle divides it into two
(a) equilateral triangles
(b) isosceles triangles
(c) right triangles
(d) triangles of equal areas

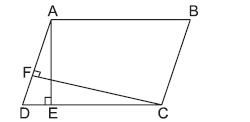
Question. In the given figure, if BC ∥ AE, CD ∥ BE, and ar(ΔBED) = 6 cm², then ar(ΔABC) is

(a) 6 cm²
(b) 8 cm²
(c) 10 cm²
(d) 12 cm²

Question. M and N are the mid-points of sides DC and AB respectively, of a rectangle ABCD. If ar(rectangle ABCD) = 48 cm², then ar(ΔEMC) is

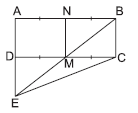
(a) 36 cm²
(b) 48 cm²
(c) 24 cm²
(d) 12 cm²

Question. ABCD is a square. DEGH is a rectangle. Two equal parallelograms on the base DE are

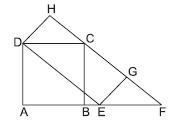
(a) DCFE and DCBA
(b) DEGC and DEFH
(c) ABCD and HDEG
(d) DEGH and DEFC

Question. ABCD is a rectangle in which AB = 8 units and AD = 3 units. If DCEF is a parallelogram, then the area of ΔEFG in sq units is

(a) 16
(b) 6
(c) 24
(d) 12

Question. In the given figure, if AD ∥ BC, then the triangle which is equal in area to ΔCOD is

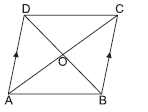
(a) ΔADC
(b) ΔBOA
(c) ΔAOD
(d) ΔCOB

Question. ABCD is a quadrilateral. A line through D, parallel to AC meets BC produced at E. If ar(ΔABE) = 36 cm2, then the ar(quad ABCD) is

(a) 18 cm²
(b) 36 cm²
(c) 72 cm²
(d) 9 cm²

Question. ABCD is a parallelogram and E and F are mid‑points of AD and BC respectively. P is any point on EF. If area of ΔEFC = 8 cm², then ar(ΔAEP + ΔBFP) is

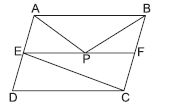
(a) 16 cm²
(b) 8 cm²
(c) 4 cm²
(d) 12 cm²

Question. PQRS and ADEQ are rectangles. RE ∥ AP.If ar(ACPQ) = 25 cm² and ar(ABEP) = 10 cm²,then ar(PQRS) is

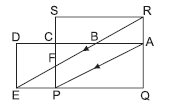
(a) 25 cm²
(b) 10 cm²
(c) 35 cm²
(d) 30 cm²

Question. ABCD is a quadrilateral whose diagonal AC divides it into two parts, equal in area, then ABCD
(a) is a rhombus
(b) is a parallelogram
(c) is a rectangle
(d) need not be any of (a), (b) or (c)

Question. ABCD is a parallelogram. O is any point on diagonal BD. If ar(ΔDOP) = 8 cm², ar (ΔBOS) = 3 cm² and ar(ΔAPS) = 6 cm², then ar(∥gm ABCD) is

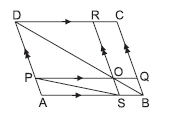
(a) 33 cm²
(b) 45 cm²
(c) 46 cm²
(d) 34 cm²

Question. P is any point on the base BC of ΔABC. D is the mid-point of BC. DE is drawn parallel to PA. If ar (ΔABC) = 12 cm², then ar(ΔEPC) is

(a) 4 cm²
(b) 8 cm²
(c) 9 cm²
(d) 6 cm²

Question. ABCD is a parallelogram in which DC is produced to P such that DC = CP. AP intersects BC at Q. If ar(ΔBQD) = 3 cm², then ar(∥ gm ABCD) is

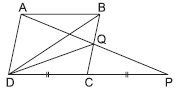
(a) 9 cm²
(b) 12 cm²
(c) 15 cm²
(d) 6 cm²

Question. PQR is a triangle. S is any point on a line through P parallel to QR. If T is any point on a line through R parallel to SQ, then the three triangles equal in area are

(a) ΔPQR, ΔQSR, ΔQST
(b) ΔPQR, ΔQSR, ΔQRT
(c) ΔQRT, ΔSRT, ΔQSR
(d) ΔQSR, ΔTSR, ΔPQR

Question. PQRS is a parallelogram whose diagonals PR and SQ intersect at O. A line segment through O meets PQ at A and SR at B. If ar(∥ gm PQRS) = 25 cm², then ar (quad SBAP) is
(a) 12 cm²
(b) 50 cm²
(c) 25 cm²
(d) 12.5 cm²

Question. In the given figure, ABCD is a parallelogram. If ar(ΔBAP) = 10 cm² and ar(ΔCPD) = 30 cm², then ar(∥gm ABCD) is

(a) 40 cm²
(b) 80 cm²
(c) 60 cm²
(d) 100 cm²

Question. ABCD and ABFE are parallelograms as shown in the figure. If ar(∥ gm ABCD) = 24 cm² and ar (∥ gm ABFE) = 18 cm², then ar(quad EFCD) is

(a) 33 cm²
(b) 42 cm²
(c) 30 cm²
(d) 36 cm²

Question. In the given figure, ABCD is a rectangle and EFGH is a trapezium DE = CH. If ar(rect ABCD) = 26 cm², then ar(trap EFGH) is

(a) 52 cm²
(b) 26 cm²
(c) 39 cm²
(d) 34 cm²

Question. PQRS is a trapezium. A is any point on PQ and AB ∥ QR. If ar(ΔPBQ) = 17 cm², then ar(ΔASR) is

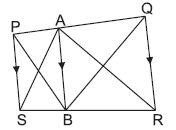
(a) 17 cm²
(b) 8.5 cm²
(c) 10 cm2
(d) 18.5 cm²

Question. ABCD is a parallelogram. P is the mid-point of AB. BD and CP intersect at Q. CQ : QP = 3 : 1. If ar(ΔBQC) = 10 cm², then ar(∥ gm ABCD) is

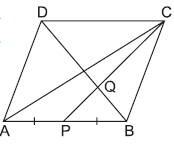
(a) 130 cm²
(b) 160 cm²
(c) 120 cm²
(d) 90 cm²

Question. In the given figure, QA = AB = BC = CR. If ar(ΔPQR) = 24 cm², then ar(ΔPAR) is

(a) 18 cm²
(b) 12 cm²
(c) 20 cm²
(d) 16 cm²

Question. ABCD is a parallelogram. M is any point on AD.P is the mid-point of BM. If the area of parallelogram ABCD = 28 cm², then the area of ΔMPC is

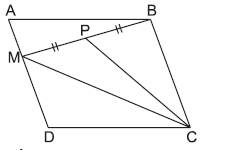
(a) 14 cm²
(b) 12 cm²
(c) 7 cm²
(d) 16 cm²

Question. ABCD, ABEF and AGHF are parallelograms. If ar(∥gm ABCD) = 23 cm², then ar(DFGH) is

(a) 12 cm²
(b) 12.5 cm²
(c) 11.5 cm²
(d) 23 cm²

Question. In the given figure, if ar (∥gm ABEF) = ar (∥gm ABCD) = 50 c m² , AFGH is a parallelogram and points E, B, G and H are collinear points, then ar(∥gm AFGH) is

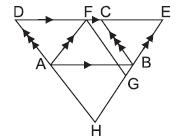
(a) 25 cm²
(b) 50 cm²
(c) 100 cm²
(d) 75 cm²

We hope the above multiple choice questions for Class 9 Mathematics for Chapter 9 Areas of Parallelogram and Triangle provided above with answers based on the latest syllabus and examination guidelines issued by CBSE, NCERT and KVS are really useful for you. Areas of Parallelogram and Triangle is an important chapter in Class 9 as it provides very strong understanding about this topic. Students should go through the answers provided for the MCQs after they have themselves solved the questions. All MCQs have been provided with four options for the students to solve. These questions are really useful for benefit of Class 9 students. Please go through these and let us know if you have any feedback in the comments section.