SECTION – A

1. If

Solution: We have

2. Find the angle between the vectors î – ĵ and – k̂ .
Solution: We’ve

3. Find the distance of a point (2, 5, –3) from the plane r̅.(6î – 3ĵ + 2k̂) = 4 .
Solution: We have

4. Write the element a₁₂ of the matrix A = [aij ]_2×2 , whose elements a_ij are given by a_ij = e^2ix sin jx .
Solution: Since a_ij = e^2ix sin jx so, a₁₂ = e^2x sin 2x .

5. Find the differential equation of the family of lines passing through the origin.
Solution: The equation of the family of lines passing through the origin is y = mx…(i)
On diff. w. r. t. x, dy/dx = m Replacing value of m from (i), we get : dy/dx = y/x .

6. Find the integrating factor for the following differential equation : x log x dy/dx + y = 2 log x .
Solution: 

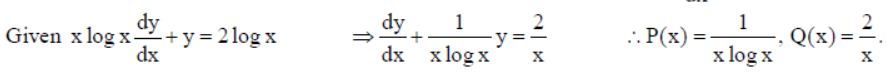
SECTION – B

7. If

Solution: 

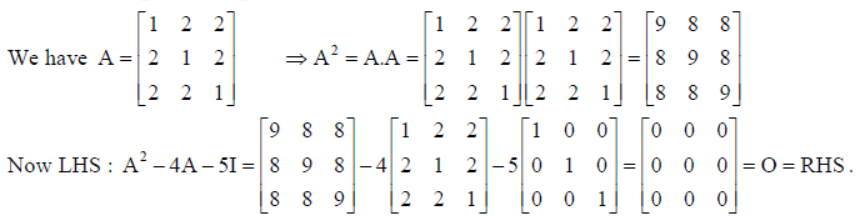
OR

If A =

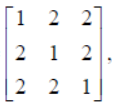
then show that A² – 4A – 5I = O, and hence find A^-1 .
Solution: We have A =

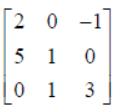
Using elementary row operations, A = I A we have,

8. Using the properties of determinants, solve the following for x :

Solution: 

9. Evaluate :

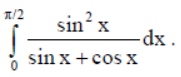
Solution: 

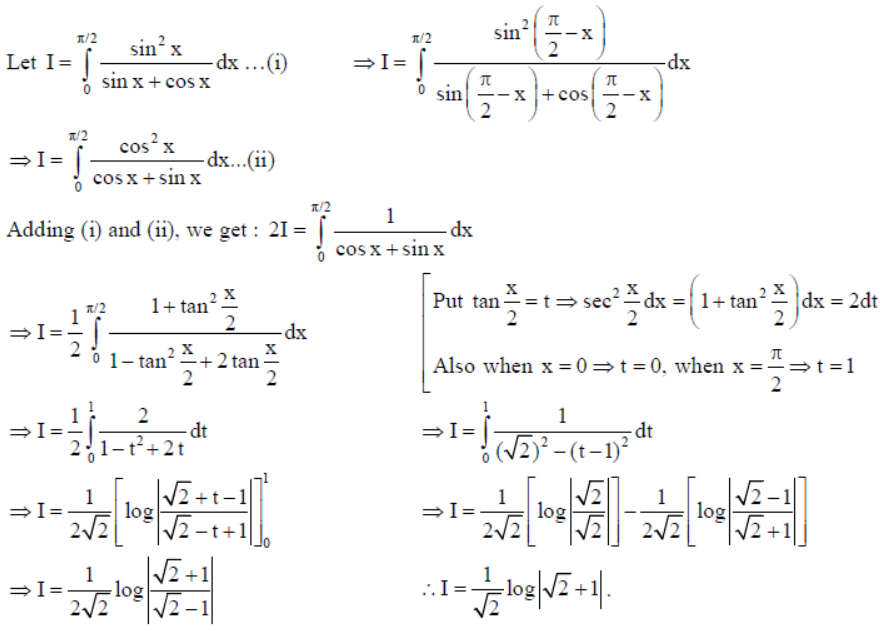
OR

Evaluate

Solution: 

10. Evaluate :

Solution:  

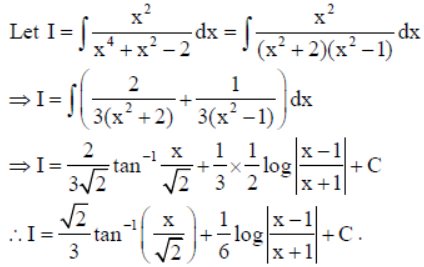
11. In a set of 10 coins, 2 coins are with heads on both the sides. A coin is selected at random from this set and tossed five times. If all the five times, the result was heads, find the probability that the selected coin had heads on both the sides.
Solution: Let E₁ and E₂ be the events that two headed coin and unbiased coin is chosen respectively. Also let E be the event that all 5 tosses are heads.

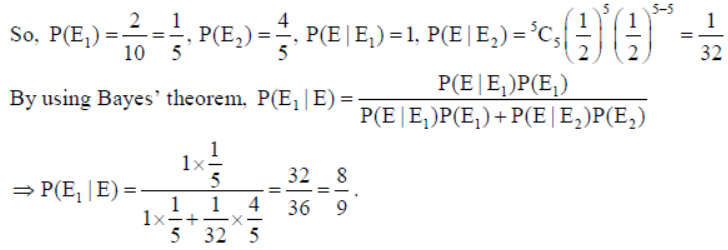
OR

How many times must a fair coin be tossed so that the probability of getting at least one head is more than 80%.
Solution: Let the coin is tossed n times ∴ Probability of getting head, p = 1/2, q = 1 – p = 1/2.

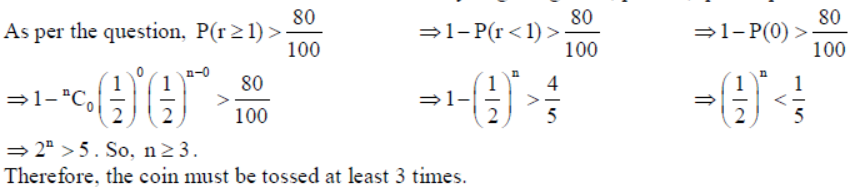
12. Find x such that the four points A (4, 1, 2), B (5, x, 6), C (5, 1, –1) and D(7, 4, 0) are coplanar.
Solution: Given A (4, 1, 2), B (5, x, 6), C (5, 1, –1) and D(7, 4, 0)

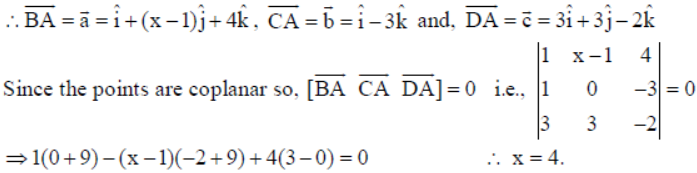
13. A line passing through the point A with position vector a̅ = 4î + 2ĵ + 2k̂is parallel to the vector b̅ = 2î + 3ĵ + 6k̂. Find the length of the perpendicular drawn on this line from a point P with position vector r̅1 = î + 2ĵ + 3k̂.
Solution: Equation of the line through a̅ = 4î + 2ĵ + 2k̂is parallel to b̅ = 2î + 3ĵ + 6k̂is

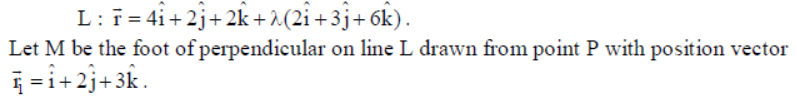
14. Solve for x : sin^-1|(1-x)-2sin^-1 x = π/2 .
Solution:

OR

Show that :

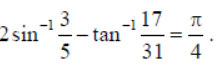
Solution: 

15. If y = e^ax cos bx , then prove that d²y/dx² -2a dy/dx + (a²+b²) y = 0
Solution:  

16. If x^x + x^y + y^x = a^b , then find dy/dx .
Solution: 

17. If x = a sin 2t(1+ cos²t) and y = bcos²t(1- cos²t) , then find dy/dx at t = π/4 
Solution: We have x = a sin 2t(1+ cos²t) and y + bcos2t(1- cos²t)

18. Evaluate :

Solution: 

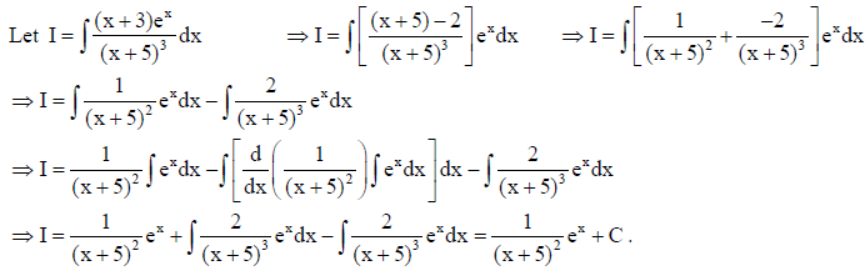
19. Three schools X, Y and Z organized a fete (mela) for collecting funds for flood victims in which they sold hand-held fans, mats and toys made from recycled material, the sale price of each being ₹ 25, ₹ 100 and ₹ 50 respectively. The following table shows the number of articles of each type sold :

Using matrices, find the funds collected by each school by selling the above articles and the total funds collected. Also write any one value generated by the above situation.
Solution: Let the funds collected by schools X, Y and Z be x, y and z (in ₹) respectively.

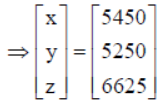
By equality of matrices, we get : x = 5450, y = 5250, z = 6625 .
So the funds collected by school X is ₹5450, by school Y is ₹ 5250 and by school Z is ₹6625.
And, total funds collected = ₹17325.

SECTION – C

Q20. Let A = QxQ, where Q is the set of all rational numbers, and * be a binary operation on A defined by (a, b)*(c,d) = (ac, b + ad) for (a, b),(c,d)∈A. Then find
(i) The identity element of * in A.
(ii) Invertible elements of A, and hence write the inverse of elements (5, 3) and (1/2 ,4)
Solution: Given A = QxQ, where Q is the set of all rational numbers, and * be a binary operation on A defined by (a, b)*(c,d) = (ac, b + ad) for (a, b),(c,d)∈A.
(i) Let (e,e’) be the identity element of * in A. Then (a, b)*(e,e’) = (a,b) = (e,e’)*(a, b)

OR

Let f :W → W be defined as

Show that f is invertible and find the inverse of f. Here, W is the set of all whole numbers.
Solution: Given f :W → W given by

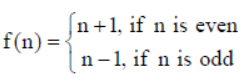
For one-one : Let n,m∈W.
If n and m are both even, then f (n) = f (m)⇒ n +1 = m+1 = n = m
If n and m are both odd, then f (n) = f (m)⇒ n +1 = m+1 = n = m
Thus in both the cases, we have f (n) = f (m)⇒ n = m.
If n is odd and m is even then f (n) = n -1 is even and f (m) = m+1 is odd.
Therefore, n ≠ m ⇒ f (n) ≠ f (m) .
Similarly if n is even and m is odd, then also n ≠ m ⇒ f (n) ≠ f (m) .
Hence f is one-one.
For onto : Let n ∈ W be an arbitrary element. If n is an odd natural number then ∃ an even natural number n -1 ∈ W (domain) s. t. f (n -1) = n – 1+1= n.
If n is an even natural number then ∃ an odd natural number n + 1∈ W (domain) s. t.
f (n +1) = n +1-1 = n.
Also note that f (1) = 0.
So every element of W (codomain) has its pre-image in the domain W.
Hence f is onto. Therefore, f is bijection.
Now let n,m ∈ W s. t. f (n) = m which implies that n + 1= m,if n is even and n – 1 = m, if n is odd .

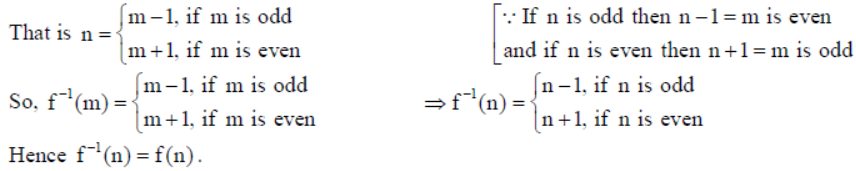
21. Sketch the region bounded by the curves y = √5 – x² and y = |x -1| and find its area using integration.
Solution: 

22. Find the particular solution of the differential equation 
x²dy = (2xy+y²)dx , given that y =1 when x =1.
Solution: 

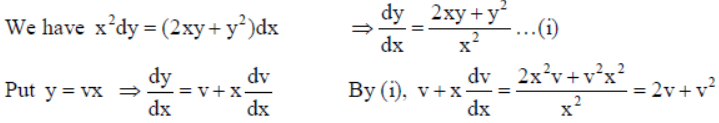
OR

Find the particular solution of the differential equation (1+x²)dy/dx = (e^mtan-1 x – y) , given that y =1 when x = 0 .
Solution: 

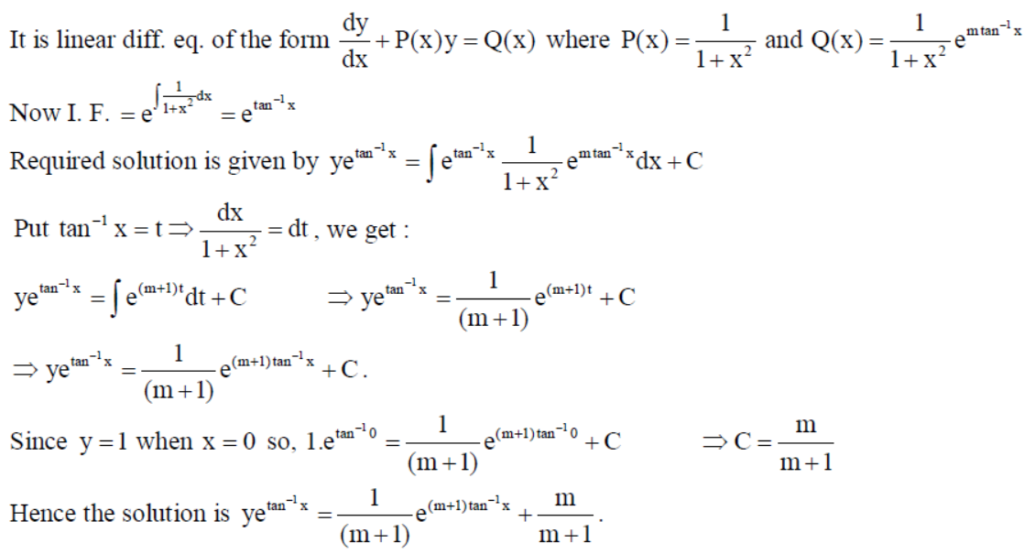
23. Find the absolute maximum and absolute minimum values of the function f given by f (x) = sin² x – cos x, x ∈ [0,π].
Solution: Given f (x) = sin² x – cos x, x∈[0,π]
⇒ f ‘(x) = 2sin x cos x + sin x = sin x(2cos x +1)
For critical points, f ‘(x) = sin x(2cos x +1) = 0 ⇒ sin x = 0, 1+ 2cos x = 0 
⇒ x = 0, 2π/3 , π ∈[0,π]
Now, f (0) sin2 0 – cos0 = -1 , f(2π/3) = sin2 2π/3 – cos 2π/3 = 3/4 + 1/2 = 5/4 ,
f (π) = sin2 π – cosπ =1.
So, absolute maximum value = 5/4 and absolute minimum value = -1.

24. Show that the lines :

Also, find the equation of the plane containing these lines.
Solution: 

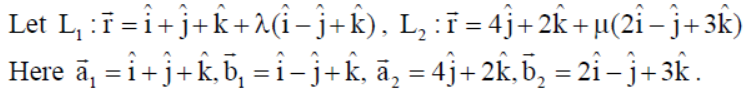
If these lines are coplanar then, (a̅₂ – a̅₁).(b̅₁ x b̅₂) = 0

25. Minimise and maximize z = 5x + 2y subject to the following constraints :
x – 2y ≤ 2
3x + 2y ≤ 12
– 3x + 2y ≤ 3
x ≥ 0, y ≥ 0.
Solution: We have z = 5x + 2y
And subject to the constraints :

x – 2y ≤ 2
3x + 2y ≤ 12
– 3x + 2y ≤ 3
x ≥ 0, y ≥ 0.

Hence, the maximum value of z is 19 at (7/2,3/4)
And, the minimum value of z is 3 at(0,3/2)

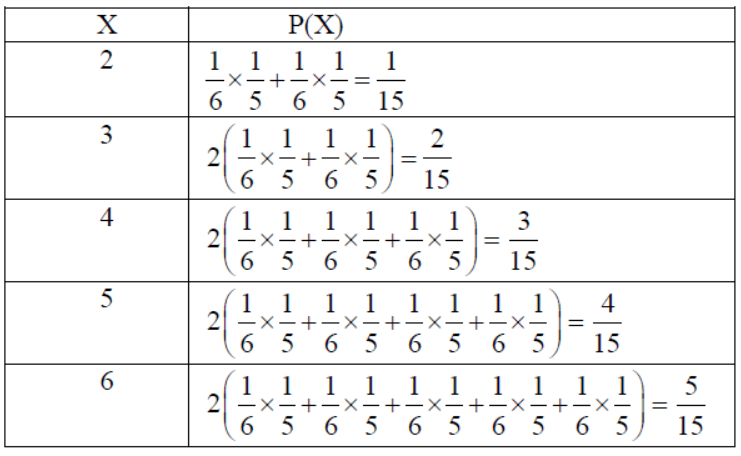
26. Two numbers are selected at random (without replacement) from first six positive integers. Let X denote the larger of the two numbers obtained. Find the probability distribution of X. Find the mean and variance of this distribution.
Solution: Since X denotes the larger of the two numbers obtained from 1, 2, 3, 4, 5 and, 6.
So values of X : 2, 3, 4, 5, 6.