Sample Paper Class 12 Mathematics Term 1 Set D
Section A
In this section, attempt any 16 questions out of Questions 1-20. Each question is of 1 mark weightage.
1. The point at which the tangent to the curve y =√4x-3 – 1 has its slope 2/3 , is
(a) (2, 3)
(b) (3, 2)
(c) (3, 1)
(d) (1, 3)
Answer
B
2. The value of
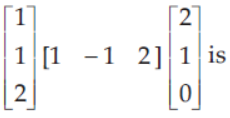

Answer
C
3. If for any 2 x 2 square matrix A, A adj(A) =

(a) 64
(b) 1
(c) 5
(d) 32
Answer
B
4. If

then the value of xyz is
(a) 10
(b) 12
(c) 15
(d) 0
Answer
B
5. If x = sinθ, y = tanθ, then dy/dx at θ = π/3 is equal to
(a) 1
(b) 8
(c) 3
(d) 4
Answer
B
6. If A is a square matrix such that A2 = I , then A +A-1 is equal to
(a) A+ I
(b) A
(c) 0
(d) 2A
Answer
D
7. The equation of tangent to the curve y = 2x2 + 3 sin and (0, 0) is
(a) y = 3x
(b) y = – 3x
(c) x = 3y
(d) x = – 3y
Answer
A
8. If [x 1]

= 0 , then x2 is equal to
(a) 2
(b) 4
(c) 8
(d) 1
Answer
B
9. The value of cos(1/2 sin-1 √3/2) is
(a) 1/2
(b) √3/2
(c) 1/√2
(d) None of these
Answer
B
10. The principal value of sin-1(-√3/2) is
(a) -2π/3
(b) -π/3
(c) 4π/3
(d) 5π/3
Answer
B
11. Let X be the set of all persons living in a city. Persons x, y in X are said to be related as x < y, if y is atleast 5 yr older than x. Which one of the following is correct?
(a) The relation is an equivalence relations on X
(b) The relation is transitive but neither reflexive nor symmetric
(c) The relations is reflexive but neither transitive nor symmetric
(d) The relation is symmetric but neither transitive nor reflexive
Answer
B
12. Let S denote set of all integers. Define a relation R on S as ‘aRb’ if ab ≥ 0, where a, b ∈ S.
Then, R is
(a) reflexive but neither symmetric nor transitive relation
(b) reflexive, symmetric but not transitive relation
(c) an equivalence relation
(d) symmetric but neither reflexive nor transitive relation
Answer
C
13. If

(a) (1, 1)
(b) (1, – 1)
(c) (- 1, 1)
(d) (- 1, – 1)
Answer
C
14. If Δ =
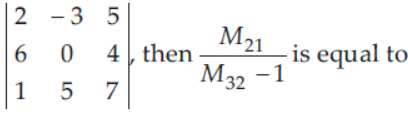
(a) 1
(b) 2
(c) 3
(d) 4
Answer
B
15. If

then x is equal to
(a) 6
(b) ± 3
(c) – 3
(d) 3
Answer
B
16. The function f (x) = log x is strictly increasing on
(a) [- 1, 0]
(b) (0, ∞)
(c) (- ∞, ∞)
(d) None of these
Answer
B
17. The function f (x) = x3 – 3x2 + 3x – 10 in the interval (- ∞, ∞) is
(a) decreasing
(b) increasing
(c) strictly increasing
(d) strictly decreasing
Answer
B
18. The slope of the tangent to the curve x = 3t2 + 1 , y = t3 – 1 at x = 1 is
(a) – 1
(b) 1
(c) 0
(d) 2
Answer
C
19. If x

(a) 4
(b) 16
(c) 2
(d) 1
Answer
B
20. The point on the curve y = x2 – 4x + 5, where tangent to the curve is parallel to the X-axis is
(a) (0, 5)
(b) (- 1, 0)
(c) (1, 2)
(d) (2, 1)
Answer
D
Section B
In this section, attempt any 16 questions out of Questions 21-40. Each question is of 1 mark weightage.
21. If y =(cot-1 x2) and (x2+1)2 d2y/dx2 + 2x (x2+1) dy/dx = k , then K is equal to
(a) 1
(b) 2
(c) 5
(d) 7
Answer
B
22. If A =

then A2 + 3A – 2I is equal to

Answer
A
23. The equation of normal at the point (1, 1) on the curve 2y + x2 = 3 is
(a) x + y = 0
(b) x – y = 0
(c) x + y + 1 = 0
(d) x – y = 1
Answer
B
24. If x = a(t – sin t), y = a(1 + cos t), then dy/dx at t = π/2 is equal to
(a) – 1
(b) 0
(c) 3
(d) 8
Answer
A
25. If y = log(xy), then dy/dx at (1, 2) is equal to
(a) 1
(b) 2
(c) 3
(d) 4
Answer
B
26. The maximum value of the function f (x) = -(x-1)2 + 8 is
(a) 7
(b) 8
(c) 0
(d) 1
Answer
B
27. The value of sin[π/2 – sin-1(-√3/2)] is
(a) 1/2
(b) -1/2
(c) 1
(d) – 1
Answer
A
28. The function f : R → R defined by f(x) = x/x2+1 , ∀ x ∈ R is
(a) one-one
(b) not one-one
(c) bijective
(d) None of these
Answer
B
29. Let f : [0, 1] → [0, ∞) be defined by f(x) = x/1+x , then f is
(a) one-one but not onto
(b) onto but not one-one
(c) both one-one and onto
(d) neither one-one nor onto
Answer
A
30. If A =

(a) AB= BA
(b) AB ≠ BA
(c) A2 = B
(d) None of these
Answer
A
31. If A =

then |3A|is equal to
(a) 3|A|
(b) 9|A|
(c)|A|
(d) 27|A|
Answer
B
32. If at x = 1, then function f(x) = x4 – 62x2 + ax + 9 attains its maximum value on the interval [0, 2], then the value of a is
(a) 124
(b) 120
(c) – 120
(d) 128
Answer
B
33. If y = 3 cos x + 3 sin x, then d2y/dx2 + y is equal to
(a) 0
(b) 1
(c) 2
(d) 3
Answer
A
34. If y = e-3x and d2y/dx2 = ky , then K is equal to
(a) 1/9
(b) 9
(c) 2
(d) 1
Answer
B
35. If y = 2 log sin x, then d2y/dx2 is equal to
(a) – 2cosec2 x
(b) 2 cosec 2x
(c) 2 cot2 x
(d) sec2x
Answer
A
36. If x = at2 and y = at3 , then d2y/dx2 at t = 3/4 is equal to
(a) a
(b) 1/a
(c) 4
(d) -1
Answer
B
37. If y = a cos3 t and x = a sin3 t , then dy/dx at t = π/4 is
(a) 1
(b) -1
(c) 0
(d) 2
Answer
B
38. The function f(x) = (x-1)ex + 2 on [0, ∞) is
(a) increasing
(b) decreasing
(c) strictly decreasing
(d) None of these
Answer
A
39. For real numbers x and y, define a relation R, xRy if only if x – y + √2 is an irrational number. The, the relation R is
(a) reflexive
(b) symmetric
(c) transitive
(d) an equivalence relation
Answer
A
40. The function f (x) = x3 + x2 + x + 1 has
(a) maximum value at x = – 1
(b) minimum value at x = – 1
(c) neither maximum nor minimum value
(d) None of these
Answer
C
Section C
In this section, attempt any 8 questions. Each question is of 1 mark weightage. Questions 46-50 are based on Case-Study.
41. If x = tan(1/a log y) and (1+x2) d2y/dx2 + 2x dy/dx = k dy/dx , then k is equal to
(a) a
(b) a/2
(c) 2a
(d) 1
Answer
A
42. If A =

then A50 is equal to
(a) 2 49 A
(b) 2A
(c) 49A
(d) 299 A
Answer
A
43. The function f given by f (x) = x2 – x + 1 on (- 1, 1) is
(a) strictly decreasing
(b) strictly increasing
(c) neither strictly increasing nor strictly decreasing
(d) None of these
Answer
C
44. If y = sin-1 x and (1-x2) d2y/dx2 = k dy/dx , then k is equal to
(a) x
(b) x2
(c) 1
(d) 0
Answer
A
45. If λ3 = – 2, then the value of

(a) – 11
(b) – 12
(c) – 13
(d) 0
Answer
C
CASE STUDY
Suppose a dealer in rural area wishes to propose a number of sewing machines. He has some money to invest and has space for few items for storage.
Let x denotes the number of electronic sewing machines and y denotes the number of manually operated sewing machines purchased by the dealer. For the same, constraint related to investment is given by 3x +2y ≤ 48.

And objective function is Z = 22x +18y.
And other constraints consists the following x + y ≤ 20, x, y ≥ 0.
Based on above information, answer the following questions.
46. Number of corner points of the feasible region is
(a) 3
(b) 4
(c) 5
(d) 6
Answer
B
47. Sum of values of Z at all the corner points is
(a) 1008
(b) 1104
(c) 1100
(d) 1108
Answer
B
48. To get the maximum profit (i.e. maximise Z) how many electronic sewing machines should be purchased by the dealer.
(a) 12
(b) 8
(c) 10
(d) 5
Answer
B
49. To get the maximum profit (i.e. maximise Z) how many manually operated sewing machines should be purchased by the dealer.
(a) 10
(b) 5
(c) 8
(d) 12
Answer
D
50. Z| max – Z| min is equal to
(a) 360
(b) 392
(c) 352
(d) None of these
Answer
B
