Sample Paper Class 12 Mathematics Term 1 Set C
Section A
1. If a matrix has 16 elements, then the number of its possible order is
(a) 1
(b) 5
(c) 4
(d) 2
Answer
B
2. If A is a symmetric matrix, then A5 is a
(a) symmetric matrix
(b) skew-Symmetric matrix
(c) identity matrix
(d) null matrix
Answer
A
3. The equation of tangent at (3, 22) to the curve y = x2 + 4x + 1 is
(a) 10x + y + 8 = 0
(b) 10x – y + 8 = 0
(c) 10x – y – 8 = 0
(d) None of these
Answer
C
4. The critical point of the function f (x) = 2x3 – 21x2 + 36x – 20 is/are
(a) 1
(b) 6
(c) 1, 6
(d) None of these
Answer
C
5. The interval in which f (x) = x2 + x – 2 5 is increasing is
(a) (- ∞, – 1)
(b) (- 1, ∞)
(c) (- 1, 1)
(d) R
Answer
B
6. A coin is biased so that the head is 2 times as likely to occur as tail. If the coin is tossed twice, get the probability distribution of number of tails. Hence, the mean of the distribution is
(a) 1/4
(b) 2/3
(c) 3/4
(d) 1/3
Answer
B
7. If X follows Binomial distribution with parameters n = 5, p and P (X = 2) = 9P(X = 3), then p is equal to ……… .
(a) 1/20
(b) 1/40
(c) 1/10
(d) 1/5
Answer
C
8. The income of a group of 10000 persons was found to be normally distributed with mean ₹ 1750 per month and standard deviation ₹ 50.
The percentage of persons having income exceeding ₹ 1668 is
(a) 90%
(b) 92%
(c) 89%
(d) 95%
Answer
D
9. Assume that the probability of a bomb dropped from an aeroplane will strike a certain target is 1/5. If 6 bombs are dropped, the probability that atleast 2 will strike the target is
(a) 0.301
(b) 0.3612
(c) 0.3762
(d) 0.3378
Answer
D
10. The cost of living index is always
(a) value index
(b) quantity index
(c) weighted index
(d) price index
Answer
C
11. Unit test for constructing an index number is satisfied by
(a) simple aggregative method
(b) except simple aggregative method
(c) simple average of price relative
(d) except simple average of price relative
Answer
B
12. For the given data, ∑R = 1134 , ∑W = 310 and ∑RW = 38400. Consumer price index is
(a) 123.87
(b) 140.42
(c) 118.68
(d) 133.73
Answer
A
13. If, A is a non singular matrix of order 3 and |A|= – 8, then the value of |adj A| is
(a) – 8
(b) 64
(c) – 64
(d) 24
Answer
B
14. The demand matrix which is consistent with the technology matrix


Answer
B

(a) x/y
(b) y/x
(c) – x/y
(d) – y/x
Answer
B
16. In a 600 m race, A can give a start of 6 m to B and A start of 14 m to C. In the same race B give the start to C
(a) 8.09 m
(b) 9 m
(c) 9.08 m
(d) 7.08 m
Answer
A
17. The solution set of the inequality 37 – (3x + 5) > 9x – 8(x – 3) is
(a) (- ∞,2)
(b) (- ∞, – 2)
(c) (- ∞, 2]
(d) (- ∞,- 2]
Answer
C
18. A motorboat travelling with some speed, can cover 25 km upstream and 39 km downstream in 8 h. With the same speed, it can travel 35 km upstream and 52 km downstream in 11 h. The speed of the stream is
(a) 2 km/h
(b) 3 km/h
(c) 4 km/h
(d) 5 km/h
Answer
C
19. A chemist has prepared a solution in which the volume of water is 30% of the total volume. It is observed that on adding 5 L of water in the solution, the volume of water increases to 40%. The quantity of water (in L) in original solution is
(a) 35 L
(b) 30 L
(c) 14 L
(d) 9 L
Answer
D
20. If A is a square matrix such that A2 = I , where I is the identity matrix, then what is the value of A 1?
(a) A+ i
(b) Null matrix
(c) A
(d) Transpose of A
Answer
C
Section B
21. If A and B are square matrices of the same order and BA = 5I, then B-1 is equal to

Answer
B
22. A monopolistic demand function for one of its product is p(x) = ax + b. He knows that he can sell 1400 units when the price is ₹ 4 per unit and he can sell 1800 units at a price of ₹ 2 per unit. Then, the marginal revenue function is given by

Answer
B
23. If the curve ay + x2 = 7 and x3 = y, cut orthogonally at (1, 1), then the value of a is
(a) 1
(b) 0
(c) – 6
(d) 6
Answer
D
24. A bag consists of 10 balls each marked with one of the digits 0 to 9. If four balls are drawn successively with replacement from the bag. Then, the probability that none is marked with the digit 0 is

Answer
D
25. Two biased dice are thrown together. For the first die P(6) = 1/2, the other scores being equally likely while for the second die P(1) = 2/5 and the other scores are equally likely.
The probability distribution of ‘the number of one’s seen’ is
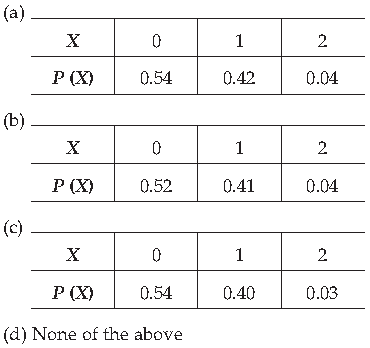
Answer
A
26. The mean weight of an item is 130 kg and the standard deviation of the item is 10 kg.
A factory produce 5000 items in a day. Assuming the normal distribution, the number of items which are expected to weight less than 142 kg is
(a) 4425
(b) 4156
(c) 3445
(d) 3872
Answer
A
27. Between the 3 pm and 5 pm the average number of phone calls per minute coming into the switchboard of a company is 3.5. The probability that during one particular minute there will be no phone call at all is
(a) 0.03
(b) 0.04
(c) 0.05
(d) 0.06
Answer
A
28. For the given data ∑p0q0 = 232, ∑p1q0 = 240, ∑p0q1 = 236 and ∑p1q1 = 255, where subscript 0 and 1 are used for base year and current year respectively, the Bowley’s index number is
(a) 1.06
(b) 1.15
(c) 1.71
(d) 1.92
Answer
A
29. The price of group of commodities is given in the following table
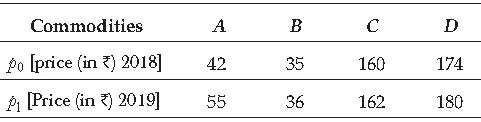
The price index for 2019 taking 2018 as base year using simple aggregative method is
(a) 101.64
(b) 110.42
(c) 105.35
(d) 112.67
Answer
C
30. Given that ∑p0q0 = 122, ∑p1q1 = 165, ∑p0q1 = 136 and ∑p1q0 = 145, where subscript 0 and 1 are used for base year and current year respectively. The Edgeworth’s index number is
(a) 119
(b) 121
(c) 124
(d) 142
Answer
A
31. For the given data, ∑p1q1 = 5453, ∑p1q0 = 5142, ∑p0q1 = 5012 and ∑p0q0 = 4956, where subscript 0 and 1 are used for base year and current year respectively, then Laspeyre’s index number is
(a) 108.86
(b) 103.75
(c) 101.10
(d) 107.08
Answer
B
32. If area of triangle is 35 sq units with vertices (2, – 6), (5, 4) and (k, 4), then k is
(a) 12
(b) – 2
(c) – 12 and – 2
(d) 12 and – 2
Answer
D
33. For the system of equations 2x – y + 3z = 9, x + y + z = 6 and x – y + z = 2 then the values of x, y and z are respectively
(a) 1, 2 and 3
(b) 1, 3 and 2
(c) 2, 1 and 3
(d) 1, 1 and 1
Answer
A
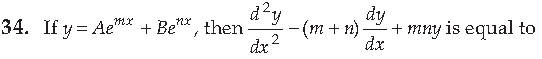
(a) 1
(b) – 1
(c) m+ n
(d) 0
Answer
D
35. Suppose a book of 614 pages contains 43 typographical errors. If these errors are randomly distributed throughout the book, the probability that 10 pages, selected at random will be free from errors is
(a) 0.974
(b) 0.947
(c) 0.479
(d) 0.497
Answer
D
36. Three pipes A, B and C together can fill a tank in 6 h. After working together for 2 h, C is closed and A and B fill the tank in 8 h. The time (in h) in which the tank can be filled by pipe C alone, is
(a) 8
(b) 9
(c) 10
(d) 12
Answer
D
37. Aman can row 9(1/3) km/h in still water and finds that it takes him thrice as much time to row up than as to row down the same distance in the river. The speed of the current is

Answer
C
38. Sanskar, Srinivas and Manohar start a business with ₹ 40000, ₹ 30000 and ₹ 70000, respectively. Srinivas and Manohar leave after 5 months and 7 months, respectively.
Who will get the largest share of profit at the end of the year of business?
(a) Sanskar
(b) Srinivas
(c) Manohar
(d) Both Manohar and Sanskar
Answer
C
39. There are three bottles of mixture of syrup and water in ratios 2 : 3, 3 : 4 and 7 : 5. 10 L and 21 L mixture are taken out from first and second bottles, respectively. How much quantity from third bottle is to be taken so that final mixture from three bottles may contain syrup and water in the ratio of 1 : 1 ?
(a) 25 L
(b) 20 L
(c) 35 L
(d) 30 L
Answer
D

Answer
A
Section C
41. The random variable X can take only the values 0, 1, 2. Given that, P(X = 0) = P(X = 1) = p and that E(X2) = E[X] = , then value of p is
(a) 1/5
(b) 3/10
(c) 2/5
(d) 1/2
Answer
D
42. The total cost function is given by

and the selling price per unit is ₹ 6. The value of x for which the profit is maximum, is
(a) 2
(b) 3
(c) 4
(d) 6
Answer
D
43. For the given data Sp0ω = 5432 and Sp1ω = 6745, where subscript 0 and 1 are used for base year and current year respectively, the index number is
(a) 121.69
(b) 128.43
(c) 124.17
(d) 129.68
Answer
C
44. In a 800 m race, B is beaten by A by 74 m and In 600 m race C is beaten by B by 50 m, then C is beaten by A in 500 m race by a distance of
(a) 85.06 m
(b) 86.06 m
(c) 84.06 m
(d) 83 m
Answer
C
45. A , B and C start a business by investing ₹ 2000, ₹ 6000 and ₹ 4000 for 6, 8 and 12 months respectively. C as an active partner receives 20% of the total profit and at the end of the year, he receives total profit of ₹ 2800. The difference between the profit received by A and B is
(a) ₹1344
(b) ₹1644
(c) ₹1400
(d) ₹1500
Answer
A
Case Study
To increase the awareness of Delhi people, the government nominates you and your friend to set a webinar. There are three auditoriums-auditorium A, auditorium Band auditorium C of a hall. There are 290 people in auditorium A, 360 people in Auditorium Band 530 people in Auditorium C.
Based on above information, answer the following questions.
46. The remainder when total number of people is divided by 7 is
(a) 3
(b) 4
(c) 5
(d) 6
Answer
B
47. The unit digit of 31180 is
(a) 6
(b) 7
(c) 8
(d) 1
Answer
D
48. The value of x in set {1, 2, 3, 4} such that number of people in auditorium A and C is equal to x (mod9) is
(a) 1
(b) 3
(c) 2
(d) 4
Answer
A
49. If all the people were arranged in 15 rows and each row have equal number of people, then the number of remaining people should be
(a) 3
(b) 5
(c) 10
(d) 13
Answer
C
50. The remainder when (290 X 360 X 530) is divided by 11 is
(a) 2
(b) 10
(c) 1
(d) 9
Answer
D
