Exam Question for Class 12 Mathematics Chapter 2 Inverse Trigonometric Functions
Please refer to below Exam Question for Class 12 Mathematics Chapter 2 Inverse Trigonometric Functions. These questions and answers have been prepared by expert Class 12 Mathematics teachers based on the latest NCERT Book for Class 12 Mathematics and examination guidelines issued by CBSE, NCERT, and KVS. We have provided Class 12 Mathematics exam questions for all chapters in your textbooks. You will be able to easily learn problems and solutions which are expected to come in the upcoming class tests and exams for standard 10th.
Chapter 2 Inverse Trigonometric Functions Class 12 Mathematics Exam Question
All questions and answers provided below for Exam Question Class 12 Mathematics Chapter 2 Inverse Trigonometric Functions are very important and should be revised daily.
Exam Question Class 12 Mathematics Chapter 2 Inverse Trigonometric Functions
Very Short Answer Type Questions
Question.

Answer.

Question. Write the principal value of
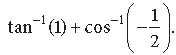
Answer.

Question. Using principal values, write the value of
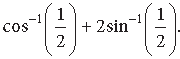
Answer. Principal value of
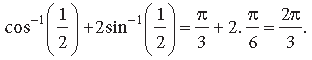
Question.
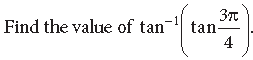
Answer.

Question. Write the principal value of
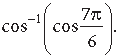
Answer.
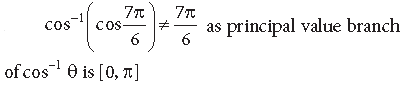
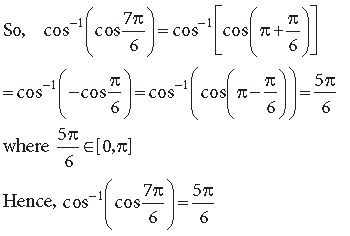
Question.
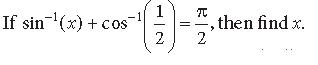
Answer.

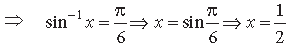
Question. Using principal value, nd the value of

Answer.
Question. If tan−1 (√3) + cot−1 (x) = π/2, then find x.
Answer.
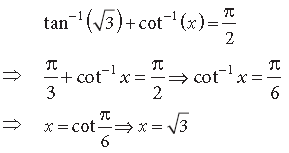
Question.
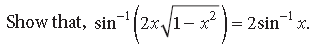
Answer.
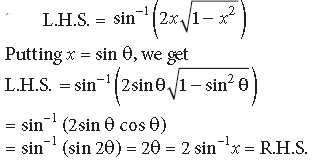
Question. Write the principal value of
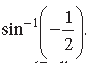
Answer.

Question. Find the principal value of

Answer. Principal value of
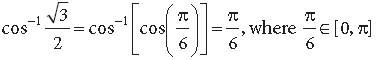
Question. Write the principal value of tan−1 (√3)− cot−1 (−√3)
Answer. tan−1 (√3)− cot−1 (−√3)
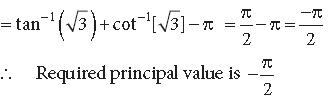
Question.
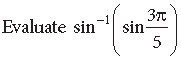
Answer. We know that, sin–1(sin x) = x
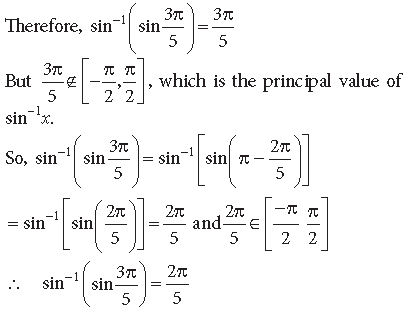
Question.
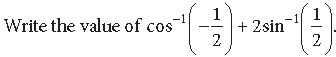
Answer.
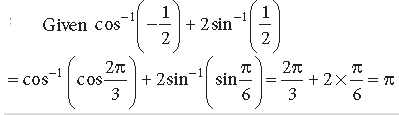
Question.

Answer.
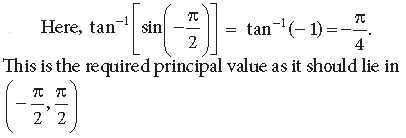
Question. Find the value of the following :
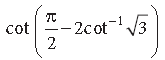
Answer.
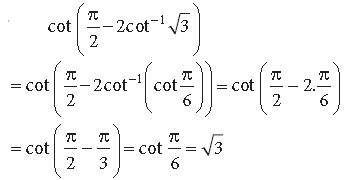
Question. If cos(tan-1 x + cot-1 √3) = 0 then the value of x is ………
Answer. cos(tan-1 x + cot-1 √3) = 0

Question. The set of values of sec-1 1/2 is ……… .
Answer. Since, domain of sec-1 x is R – (-1, 1).
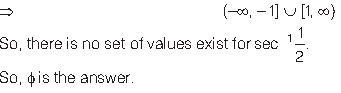
Question. The value of cos(sin-1 x + cos-1 x) where |x| ≤ 1, is ……… .
Answer.

Question.
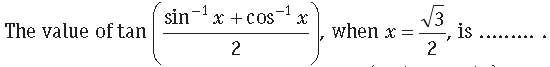
Answer.

Question. The value of cot-1 (-x ) x ∈ R in terms of cot-1 x is ……… .
Answer. We know that,

Short Answer Type Questions
Question.
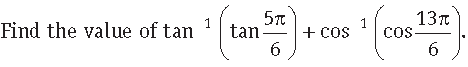
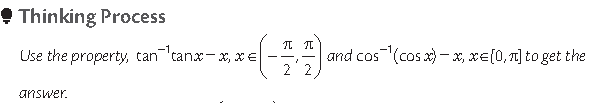
Answer.

Question.
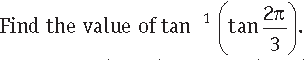
Answer.
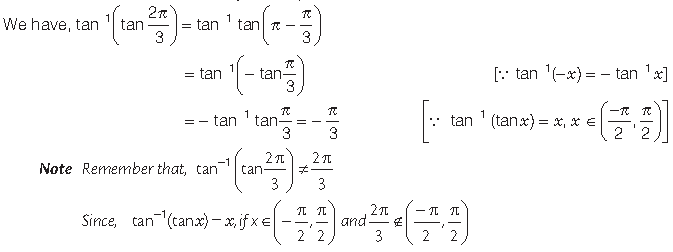
Question.
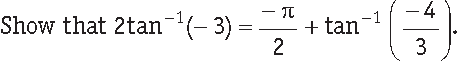
Answer.
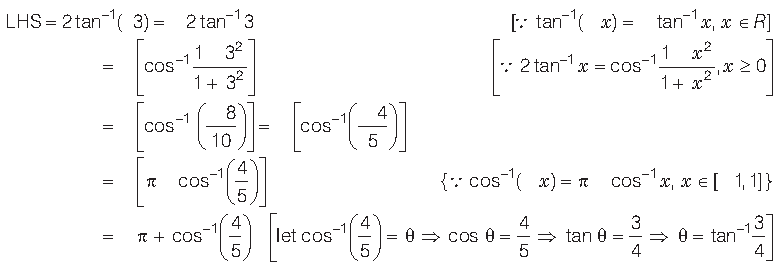
Question. If 2tan-1 (cos θ) tan-1 (2cosec θ) then show that θ = π/4, where n is any integer.
• Thinking Process
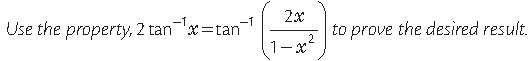
Answer.
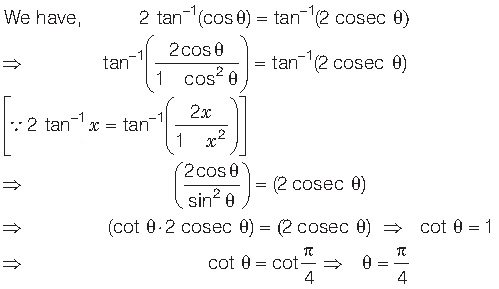
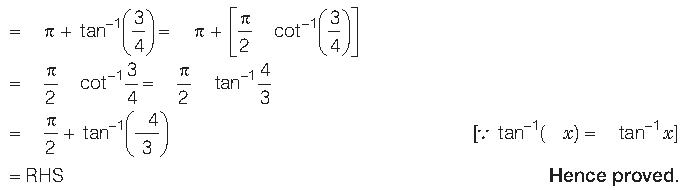
Question.

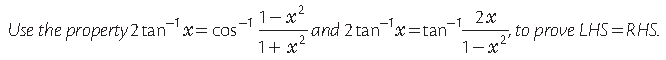
Answer.
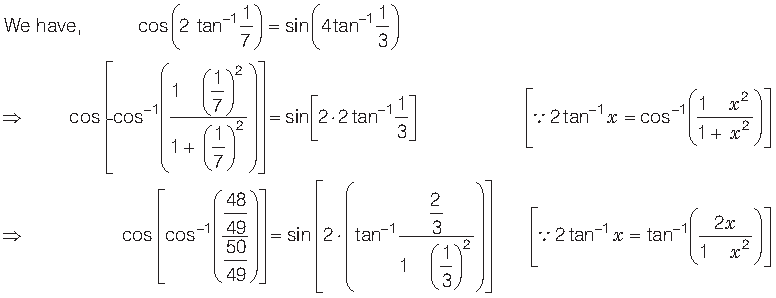

Question.
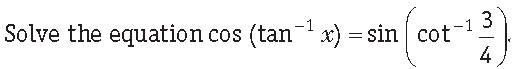
Answer.
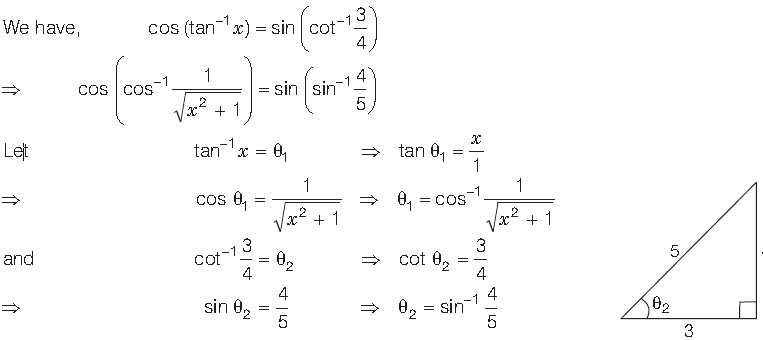
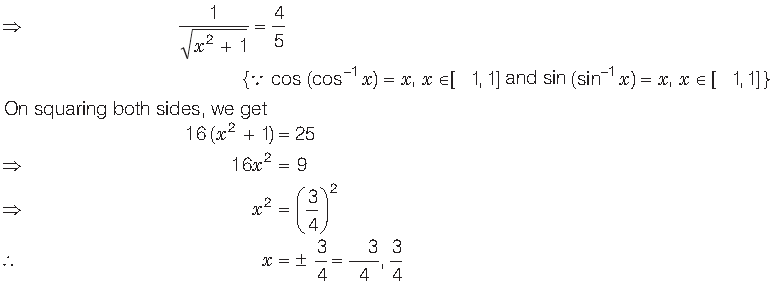
Question. Prove that
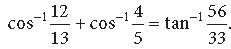
Answer.


Question. Prove that :
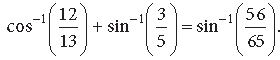
Answer.
Question. Prove that

Answer.
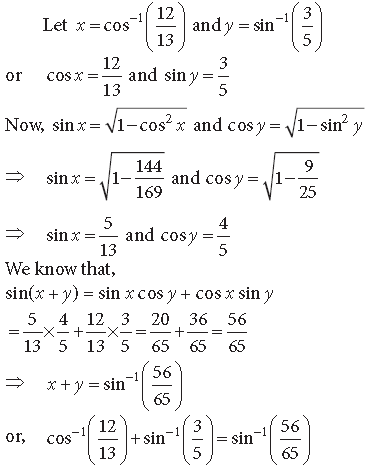
Question. Solve for x : 2 tan–1(cos x) = tan–1(2cosec x)
Answer. tan–1(cos x) = tan–1(2cosec x)
⇒ 2 tan–1 (cosx) – tan–1 (2cosecx) = 0
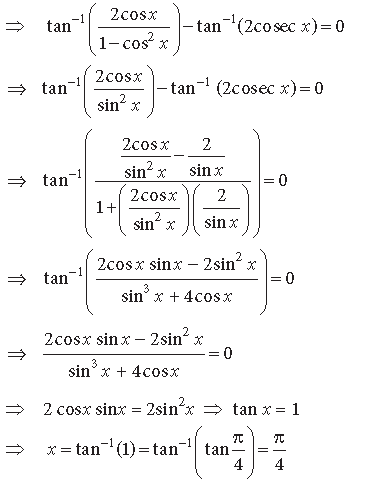
Question. Prove that
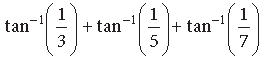
Answer.

Question. Solve the equation for x :
sin–1x + sin–1(1–x) = cos–1x
Answer.
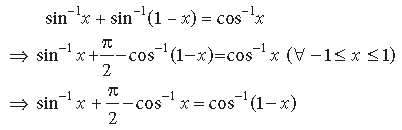
⇒ sin–1 x + sin–1 x = cos–1(1− x)
⇒ 2sin–1x = cos–1(1–x) ⇒ cos(2sin–1x) = (1 – x)
⇒ 1 – 2 sin2(sin–1 x) = (1 – x) ⇒ 2sin2 (sin–1 x) = x
⇒ 2x2 = x ⇒ 2x2 – x = 0 ⇒ x (2x –1) = 0
⇒ x = 0 or 2x – 1 = 0 ⇒ x = 0 or x = 1/2
Question.
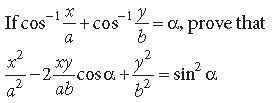
Answer.

Question. Solve for x :
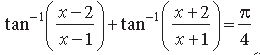
Answer.
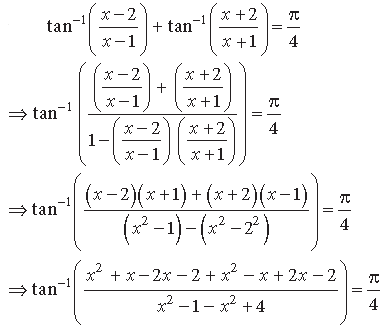

Question. Prove that :
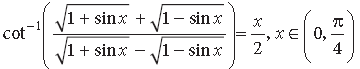
Answer. L.H.S.
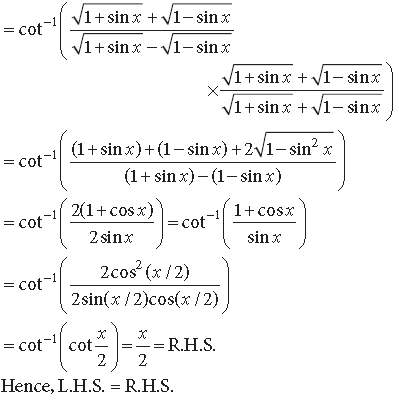
Question. If sin [cot–1 (x + 1)] = cos (tan–1 x), then find x.
Answer. We have, sin[cot–1 (x + 1)] = cos (tan–1x) … (1)
Let cot–1 (x + 1) = A and tan–1 x = B

Question. If (tan–1x)2 +(cot−1x)2 = 5π2/8 then find x.
Answer.
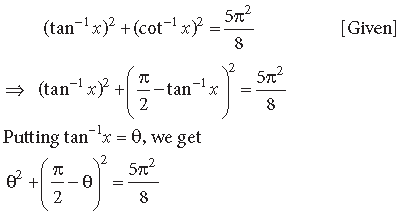
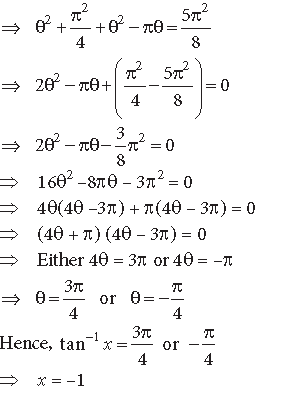
Question. Prove the following:
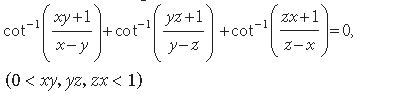
Answer. L.H.S.
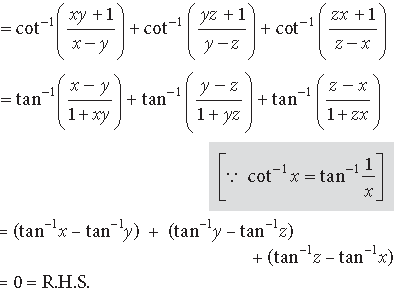
Question. Solve for x :
tan−1 (x + 1) + tan−1 (x – 1) = tan−1 8/31
Answer. We have, tan−1 (x + 1) + tan−1 (x – 1) = tan−1 8/31
Question.
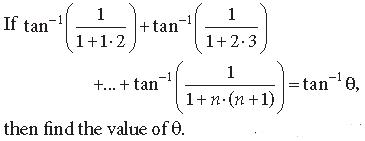
Answer.

Question. Solve for x : tan−1(2 ) + tan−1(3x) = π/4
Answer. We have, tan−1(2 ) + tan−1(3x) = π/4

Question.

Answer.

Question. Prove that
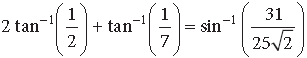
Answer.

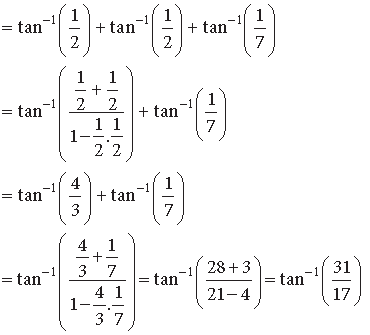

Question. Solve for x :

Answer. We have,

Question. Prove that
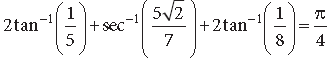
Answer. L.H.S.
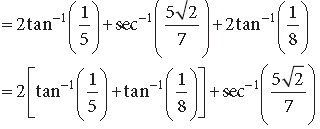
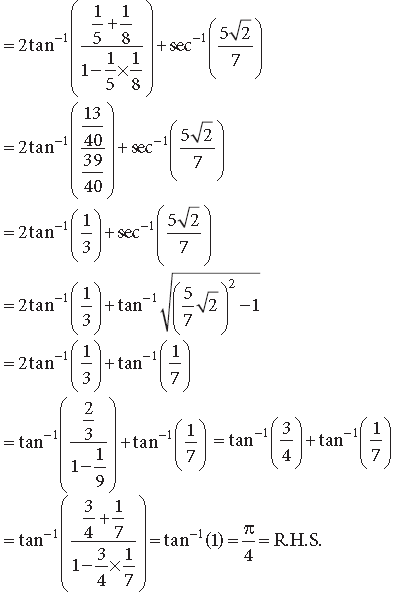
Question. Prove that

Answer. Putting x = cos θ, we get
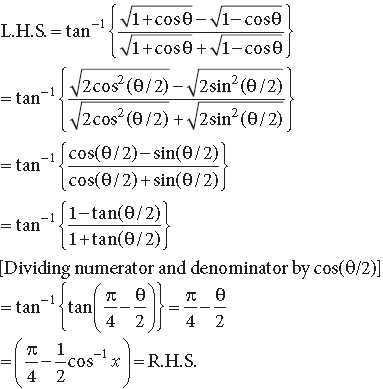
Question. Solve for x : tan−1 x + 2cot−1 x = 2π/3
Answer.

Question. Prove that :
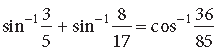
Answer.
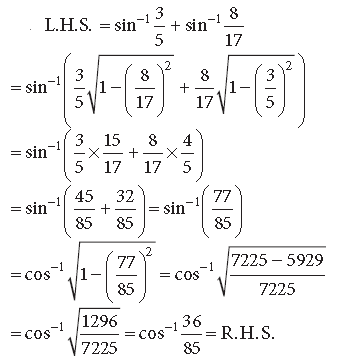
Question. Find the value of the following :
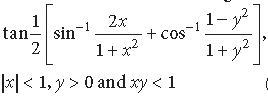
Answer.

Question. Prove that :

Answer.
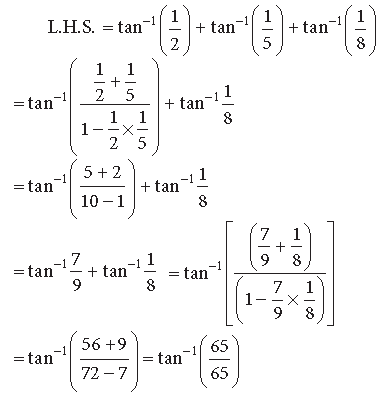
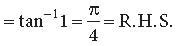
Question. Show that:

Answer.
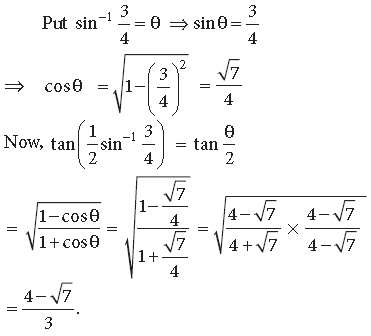

Question. Prove the following

Answer.
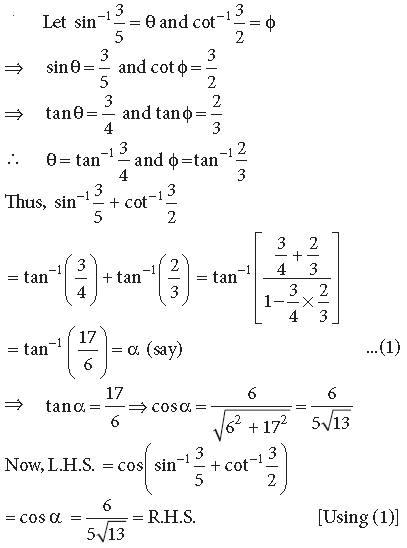
Question. Prove that :
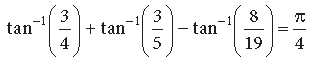
Answer.
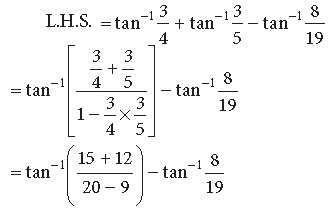
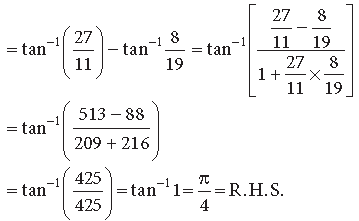
Question. Prove that :

Answer.
Question. Prove that :
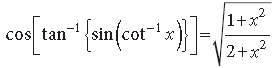
Answer.
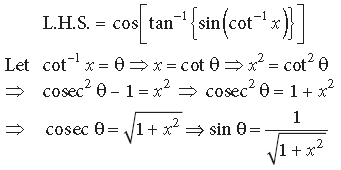

Question. Prove that :
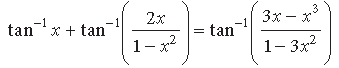
Answer.
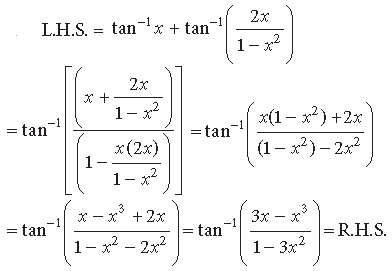
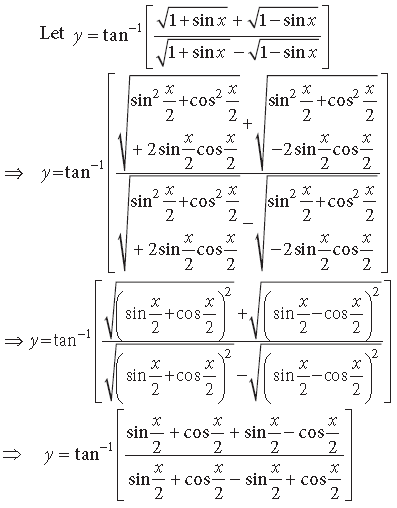
Question. Write into the simplest form:
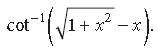
Answer.
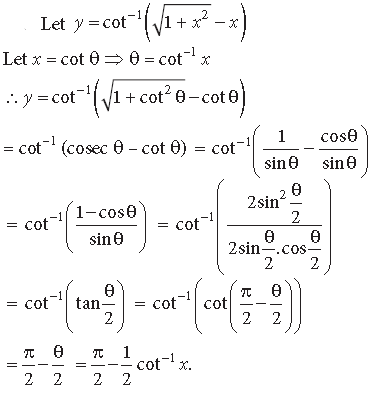
Question. Prove that :

Answer.
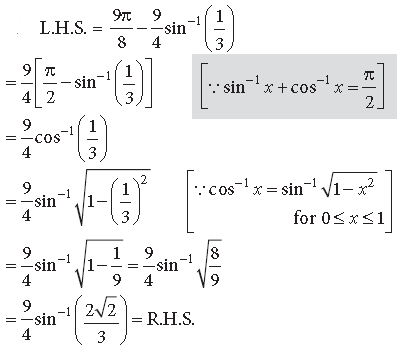
Long Answer Type Questions
Question.
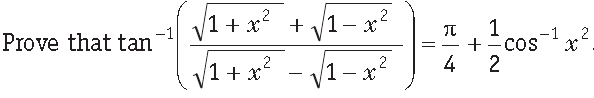
Answer. We have,
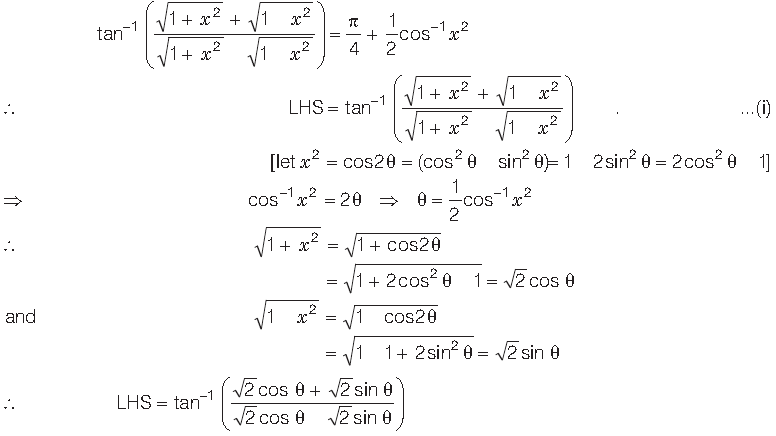

Question.
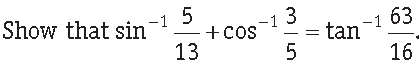
Answer.


Question.
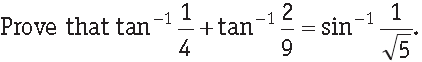
Answer.


Question. If a1, a2, a3, …, an is an arithmetic progression with common difference d, then evaluate the following expression.
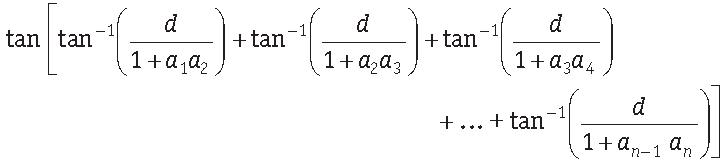
Answer.

Question. Write into the simplest form:
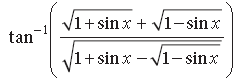
Answer.