Please refer to below Exam Question for Class 12 Mathematics Chapter 3 Matrices. These questions and answers have been prepared by expert Class 12 Mathematics teachers based on the latest NCERT Book for Class 12 Mathematics and examination guidelines issued by CBSE, NCERT, and KVS. We have provided Class 12 Mathematics exam questions for all chapters in your textbooks. You will be able to easily learn problems and solutions which are expected to come in the upcoming class tests and exams for standard 10th.

Chapter 3 Matrices Class 12 Mathematics Exam Question

All questions and answers provided below for Exam Question Class 12 Mathematics Chapter 3 Matrices are very important and should be revised daily.

Exam Question Class 12 Mathematics Chapter 3 Matrices

Very Short Answer Type Questions

Question. The product of any matrix by the scalar ……… is the null matrix.
Answer. The product of any matrix by the scalar 0 is the null matrix. i.e., 0 · A = 0.
                                                                                                                  [where, A is any matrix]

Question. For what value of x, is the matrix

Answer.

Question. If A is a matrix of order 3 x 4 and B is a matrix of order 4 x 3, find the order of matrix (AB).
Answer. the order of matrix A is 3 x 4.
the order of matrix B is 4 × 3.
∴ the order of matrix AB is 3 × 3.

question.

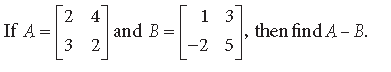
Answer.

Question. If A is a square matrix such that A² = A, then write the value of 7A – (I + A)³, where I is an identity matrix.
Answer. Here A² = A
Now, 7A – (I + A)³
= 7A – (I + A) (I + A) (I + A)
= 7A – (I + A) (I · I + I · A + A · I + (A · A))
= 7A – (I + A) (I + A + A + A)
(∵ I · A = A · I = A and A2 = A)
= 7A – (I + A) (I + 3A)
= 7A – (I · I + I · 3A) + A · I + A · (3A))
= 7A – (I + 3A + A + 3A)
= 7A – I – 7A = – I.

Question. If (2 4) ,(x/-8) = find the positive value of x.
Answer.

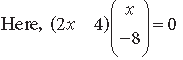
⇒ 2x · x + 4 · (–8) = 0 ⇒ 2x² – 32 = 0
⇒ x² = 16 = 42 ⇒ x = 4
which is the required positive value of x.

Question.

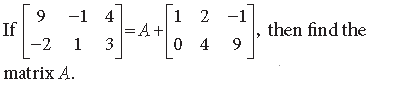
Answer.

Question.

Answer.

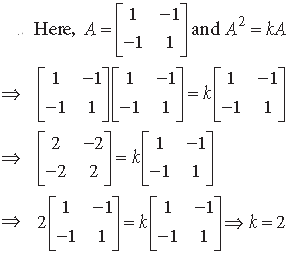
Question.

Answer.

Question. Simplify :

Answer.

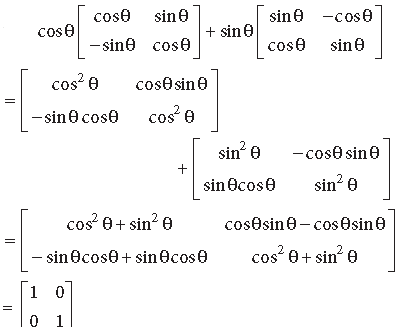
Question.

Answer.

Question. If A is a square matrix such that A² = I, then find the simplified value of (A – I)³ + (A + I)³ – 7A
Answer. Given, A² = I
Consider, (A – I)³ + (A + I)³ – 7A
= A³ – I³ – 3A²I + 3AI² + A³ + I³ + 3A²I + 3AI² – 7A
= 2A³ + 6AI² – 7A = 2AA² + 6AI – 7A
= 2AI + 6A – 7A = 2A + 6A – 7A = A

Question.

Answer.

Question. Solve the following matrix equation for x:

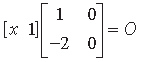
Answer.

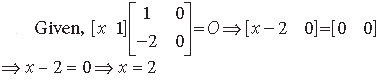
Question.

Answer.

On comparing corresponding elements of the matrices, we get a + b = 6 and b = 2
⇒ a = 4

Question. Use elementary column operation C₂ → C₂ + 2C₁ in the following matrix equation:

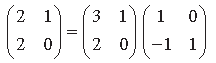
Answer.

Question. A matrix which is not a square matrix is called a ……… matrix.
Answer. A matrix which is not a square matrix is called a rectangular matrix. For example a rectangular matrix is A = [a_ij]_m X n , where m ≠ n.

Question. If A is a skew-symmetric matrix, then A² is a ……… .
Answer. If A is a skew-symmetric matrix, then A² is a symmetric matrix.
∵ A’ = – A
∴ (A²) = (A’)²
= (- A)2                                [ ∵A’ = – A]
= A²
So, A² is a symmetric matrix.

Question. If A and B are square matrices of the same order, then
(i) (AB)’ =………
(ii) (kA)’ =……… (where, k is any scalar)
(iii) [k (A – B)]’ = ………
Answer. (i) (AB)’ = B’A’
(ii) (kA)’ = k A’
(iii) [k(A – B)]’= k(A’ – B’)

Question. If A is symmetric matrix, then B’AB is ………
Answer. If A is a symmetric matrix, then B’AB is a symmetric metrix.
                                   ∵ [B’AB]’ = [B'(AB)]’
= (AB)’ (B’)’               [ ∵ (AB)’ = B’A’]
= B’A’ B
= [B’ A’B]                  [ ∵ A’ = A]
So, B’AB is a symmetric matrix.

Question. If A and B are symmetric matrices of same order, then AB is symmetric if and only if……… .
Answer. If A and B are symmetric matrices of same order, then AB is symmetric if and only if AB = BA.
∴ (AB)’
= B’A’= BA
= AB                           [ ∵ AB = BA]

Short Answer Type Questions

Question. If a matrix has 28 elements, what are the possible orders it can have?
What if it has 13 elements?
Sol. We know that, if a matrix is of order m x n, it has m x n elements, where m and n are natural numbers.
We have, m x n = 28
⇒ (m, n)= {(1, 28), (2, 14), (4, 7), (7, 4), (14, 2), (28, 1)}
So, the possible orders are 1 x 28, 2 x14, 4 x 7, 7 x 4, 14 x 2, 28 x1.
Also, if it has 13 elements, then m x n = 13
⇒ (m, n) = {(1,13), (13,1)}
Hence, the possible orders are 1 x 13, 13  x 1.

Question. Construct a 3 x 2 matrix whose elements are given by a_ij = e^ix = sin jx.
Answer.

Question. Find the values of a and b, if A = B, where

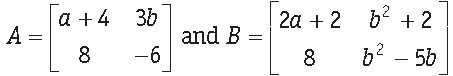
• Thinking Process
By using equality of two matrices, we know that each element of A is equal to corresponding element of B.
Answer.

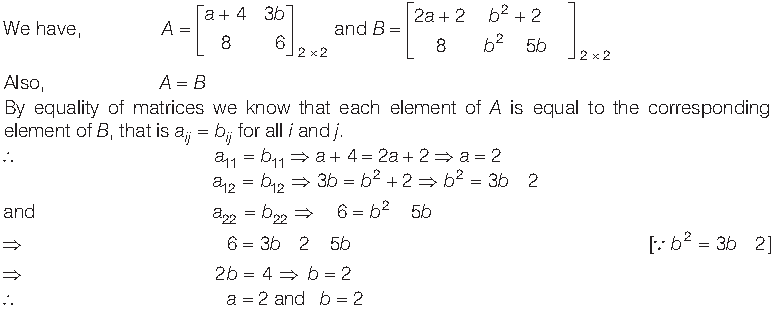
Question. Find non-zero values of x satisfying the matrix equation

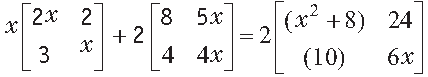
Sol. Given that,

Question.

Answer.

Question. Find the matrix A satisfying the matrix equation

• Thinking Process
We know that, if two matrices A and B of order m x n and p x q respectively are multiplied, then necessity condition to multiplication of A × B is n = p. So, by taking a matrix of correct order we can get the desired elements of the required matrix.
Answer.

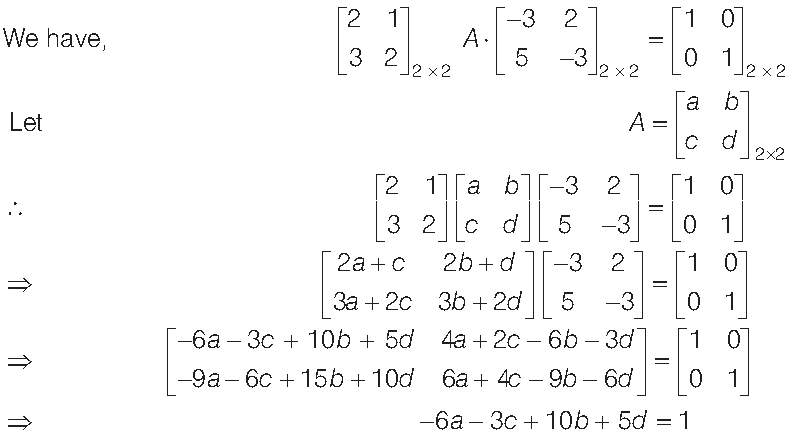
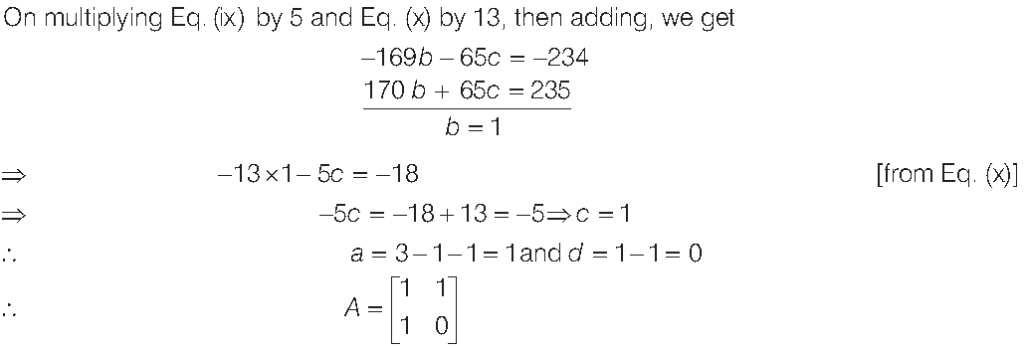
Question. If possible, find the value of BA and AB, where

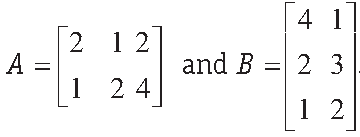
Answer.

Question. Show by an example that for A ≠ 0, B ≠ 0 and AB = 0.
Answer.

Question.

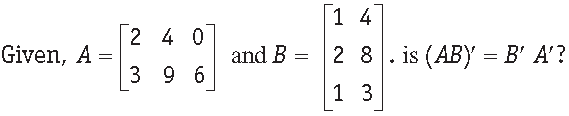
Answer.

Question.

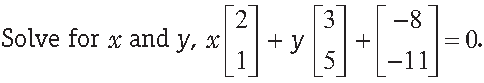
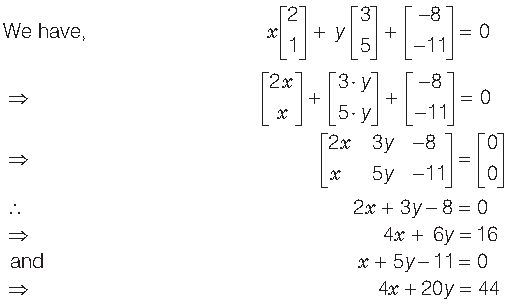
Question. If X and Y are 2 x 2 matrices, then solve the following matrix equations for X and Y

Answer. We have,

Question.

Find a matrix X such that A² – 5A + 4I + X = O
Answer. A² – 5A + 4I

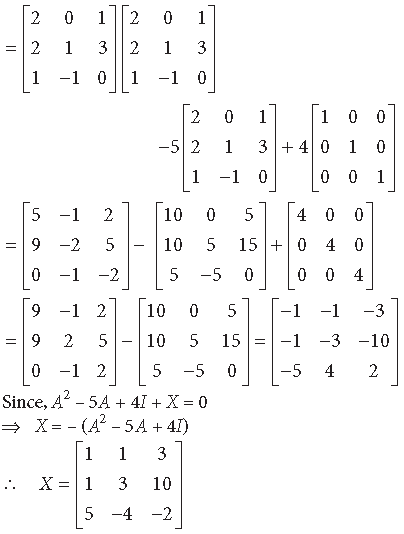
Question. Three schools A, B and C organized a mela for collecting funds for helping the rehabilitation of flood victims. They sold hand made fans, mats and plates from recycled material at a cost of ₹ 25, ₹ 100 and ₹ 50 each. The number of articles sold are given below. 
Article/School         A      B       C
Hand-fans              40    25      35
Mats                      50    40      50
Plates                    20    30      40
Find the funds collected by each school separately by selling the above articles. Also, find the total funds collected for the purpose.
Write one value generated by the above situation.
Answer. The number of articles sold by each school can be written in the matrix form as

Therefore, the funds collected by schools A, B and C are ₹ 7000, ₹ 6125 and ₹ 7875 respectively
Thus, the total fund collected
= ₹ (7000 + 6125 + 7875) = ₹ 21000
The situation highlights the helping nature of the students.

Question. To promote the making of toilets for women, an organisation tried to generate awareness through (i) house calls (ii) letters and (iii)
announcements. The cost for each mode per attempt is given below :
(i) ₹ 50 (ii) ₹ 20 (iii) ₹ 40
The number of attempts made in three villages X, Y and Z are given below:
     (i)  (ii)  (iii)
X 400 300 100
Y 300 250 75
Z 500 400 150
Find the total cost incurred by the organisation for the three villages separately, using matrices. Write one value generated by the organisation in the society.
Answer. Let ₹ A, ₹ B and ₹ C be the cost incurred by
the organisation for villages X, Y and Z respectively.
Then we get the matrix eq. as

∴ A = ₹ 30,000; B = ₹ 23,000 and C = ₹ 39,000
These are respectively the costs incurred by the organisation on villages X, Y and Z respectively.
The value generated by the organisation in the society is cleanliness.

Question.

Answer.

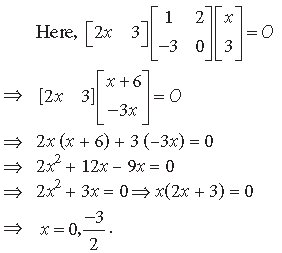
Question.

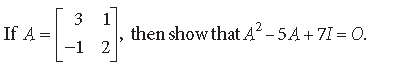
Answer.

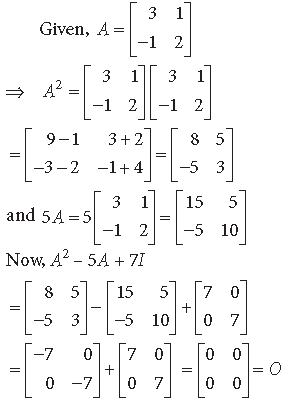
Question. For the following matrices A and B, verify that

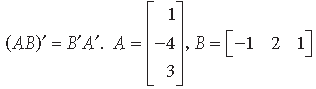
Answer.

Long Answer Type Questions

Question. Using elementary operations, find the inverse of the following matrix :

Answer. We have A = IA

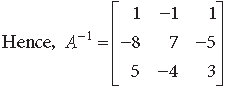
Question. Using elementary transformations, find the inverse of the matrix.

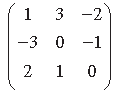
Answer.

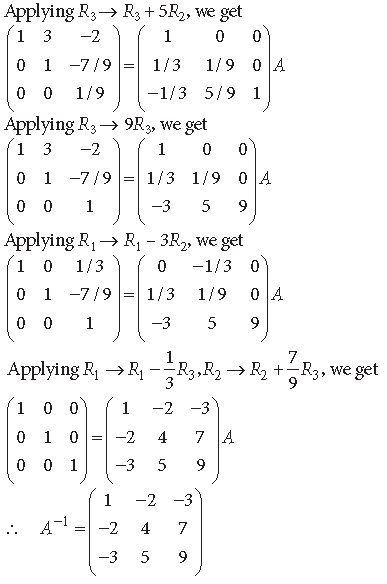
Question. Obtain the inverse of the following matrix using elementary operations :

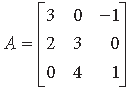
Answer.