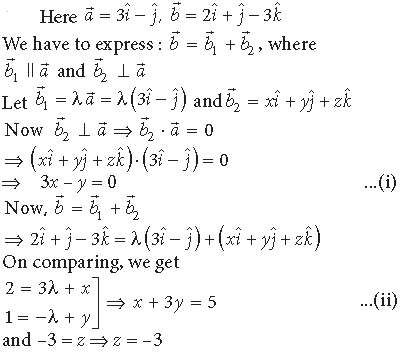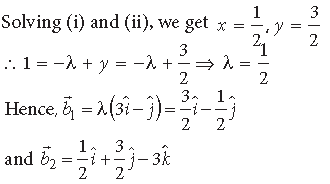Please refer to below Exam Question for Class 12 Mathematics Chapter 10 Vector Algebra. These questions and answers have been prepared by expert Class 12 Mathematics teachers based on the latest NCERT Book for Class 12 Mathematics and examination guidelines issued by CBSE, NCERT, and KVS. We have provided Class 12 Mathematics exam questions for all chapters in your textbooks. You will be able to easily learn problems and solutions which are expected to come in the upcoming class tests and exams for standard 10th.

Chapter 10 Vector Algebra Class 12 Mathematics Exam Question

All questions and answers provided below for Exam Question Class 12 Mathematics Chapter 10 Vector Algebra are very important and should be revised daily.

Exam Question Class 12 Mathematics Chapter 10 Vector Algebra

Very Short Answer Type Questions

Question. Find a vector a̅ of magnitude 5 √2, making an angle of π/4 with x-axis, π/2 with y-axis and an acute angle θ with z-axis.
Answer.

Question. Find the unit vector in the direction of the sum of the vectors 2iˆ + 3jˆ − kˆ and 4iˆ − 3jˆ + 2k
Answer.

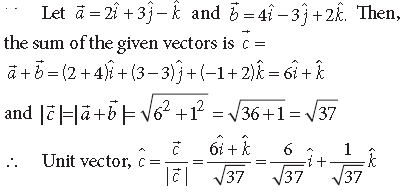
Question. Find a vector in the direction of a̅ = î – 2ĵ that has magnitude 7 units.
Answer. A unit vector in the direction of a̅ = î – 2

Question. Write the direction ratios of the vector 3a̅ + 2b̅ where
Answer.

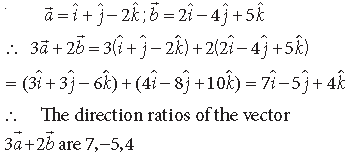
Question. Find the value of 􀁣p􀁣 for which the vectors 3iˆ + 2 jˆ + 9kˆ and iˆ − 2pjˆ + 3kˆ are parallel.
Answer.

Question. Find a vector in the direction of vector 2iˆ − 3jˆ + 6kˆ which has magnitude 21 units.
Answer.

Question. Write a unit vector in the direction of vector PQ, where P and Q are the points(1, 3, 0) and (4, 5, 6) respectively.
Answer.

Question.

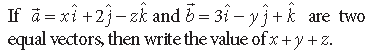
Answer. Given, a̅ = b̅

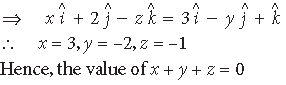
Question. Find the scalar components of the vector AB^— with initial point A(2, 1) and terminal point B(–5, 7).
Answer.

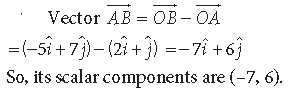
Question. Find a unit vector parallel to the sum of the vectors iˆ + jˆ + kˆ and 2iˆ − 3jˆ + 5k
Answer.

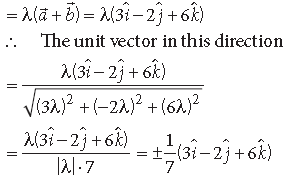
Question. Find a unit vector in the direction of the vector a̅ = 3iˆ − 2 jˆ + 6kˆ .
Answer. The given vector is a̅ = 3iˆ − 2 jˆ + 6k

Question. Write the direction cosines of the vector −2iˆ + jˆ − 5kˆ. 
Answer. We have, a̅ = −2iˆ + jˆ − 5kˆ
Direction cosines of the given vector are

Question. For what value of ‘a’, the vectors 2iˆ − 3jˆ + 4kˆ and aiˆ + 6 jˆ − 8kˆ are collinear. 
Answer. We have, 2iˆ − 3jˆ + 4kˆ and aiˆ + 6 jˆ − 8kˆ
Two vectors are collinear if and only if,

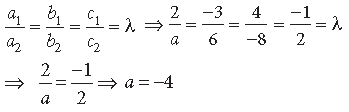
Question. Write a unit vector in the direction of the vector a̅ = 2iˆ + jˆ + 2kˆ
Answer. a̅ = 2iˆ + jˆ + 2kˆ

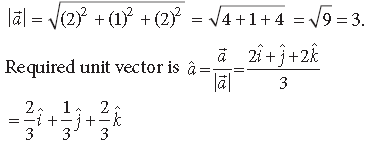
Question. Write a vector of magnitude 15 units in the direction of vector iˆ − 2 jˆ + 2kˆ.
Answer. We have, a̅ = iˆ − 2 jˆ + 2kˆ
The unit vector in the direction of given vector a̅ is

Question. Find the position vector of the mid-point of the line-segment AB, where A is the point (3, 4, –2) and B is the point (1, 2, 4).
Answer.

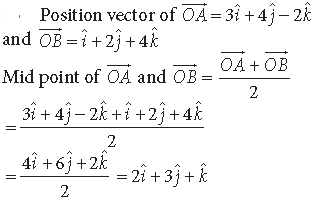
Question. Write the value of p for which a̅ = 3iˆ + 2 jˆ + 9kˆ and b̅ = iˆ + pjˆ + 3kˆ are parallel vectors.
Answer. We have, a̅ = 3iˆ + 2 jˆ + 9kˆ and b̅ = iˆ + pjˆ + 3kˆ Two vectors are parallel if

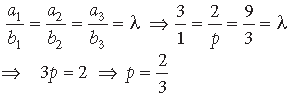
Question. Write a unit vector in the direction of a̅ = 2iˆ − 6 jˆ + 3k
Answer. We have,

Question. If P(1, 5, 4) and Q(4, 1, –2), then find the direction ratios of PQ^—
Answer. We have, P(1, 5, 4) and Q(4, 1, – 2) Since the vector is to be directed from P to Q, clearly P is the initial point and Q is the terminal point.

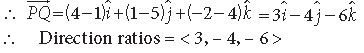
Question. If a̅ = iˆ + 2 jˆ − kˆ and b̅ = 3iˆ + jˆ − 5kˆ , then find a unit vector in the direction of a̅, – b̅,
Answer.

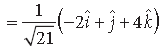
Question. Write the number of vectors of unit length perpendicular to both the vectors a̅ = 2î + ĵ + 2k̂ and b̅ = ĵ + k̂.
Answer. Given, a̅ = 2î + ĵ + 2k̂ and b̅ = ĵ + k̂.
Unit vectors perpendicular to

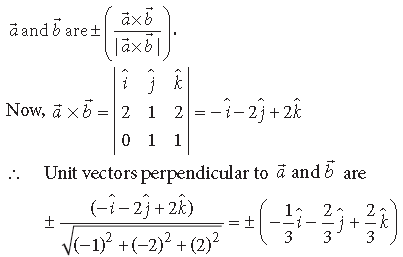
So, there are two unit vectors perpendicular to the given vectors.

Question.

Answer.

Question.

Answer.

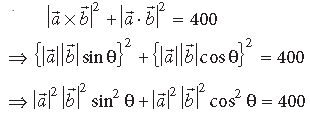
Question. Find the angle between x-axis and the vector iˆ + jˆ + kˆ.
Answer. Here, a̅ =iˆ + jˆ + kˆ and vector along x-axis is iˆ .
∴ Angle between a̅ and iˆ is given by

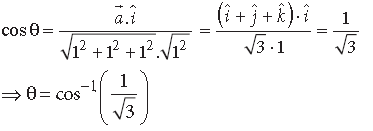
Question. Find |x̅| if for a unit vector a̅ ,

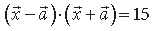
Answer.

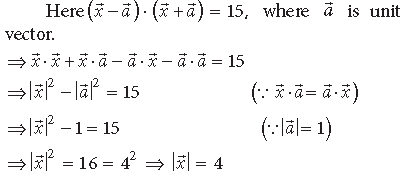
Question. Write the value of λ so that the vectors a̅ =2iˆ +λjˆ +kˆ and b̅ = iˆ −2 jˆ +3kˆ are perpendicular to each other.
Answer.

Question. Write the projection of b̅ + c̅ on a̅, where a̅ = 2iˆ −2 jˆ + kˆ, b̅ = iˆ +2 jˆ −2kˆ and c̅ = 2iˆ − jˆ + 4k̂
Answer. a̅ = 2iˆ −2 jˆ + kˆ, b̅ = iˆ +2 jˆ −2kˆ and c̅ = 2iˆ − jˆ + 4k̂

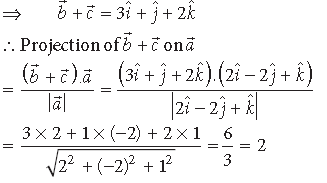
Question. Find ‘λ’ when the projection of

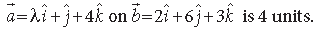
Answer.

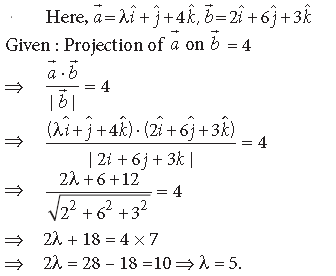
Question. Write the value of (î x ĵ) · kˆ + î · ĵ. 
Answer. (î x ĵ) · kˆ + î · ĵ  = kˆ · kˆ + iˆ · jˆ = 1 + 0 = 1

Question. Write the value of (kˆ x ĵ) · î + ĵ · kˆ
Answer. (kˆ x ĵ) · î + ĵ ·kˆ = −iˆ · iˆ + jˆ · kˆ = −1 + 0 = −1

Question. Write the value of (kˆ x î) · ĵ + î · kˆ
Answer. (kˆ x î) · ĵ + î · kˆ = ĵ · ĵ +0 = 1 + 0 = 1

Question. Write the angle between two vector a̅ and b̅ with magnitudes √3 and 2 respectively having
a̅ · b̅ = √6.
Answer. Let θ be the angle between a̅ and b̅, then

Question. Write the projection of the vector iˆ − jˆ on the vector iˆ + jˆ.
Answer.

Question.

Answer.

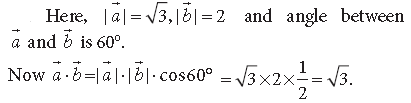
Question. If a̅ and b̅ are two vectors such that |a̅ · b̅| = |a̅ x b̅| then find the angle between a̅ and b̅
Answer.

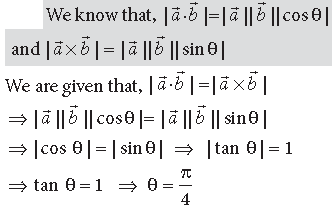
Question. Find λ, if (2î + 6 ĵ +14k̂) λ (î − ĵ + 7k̂) = 0.
Answer.

Question. If |a̅| = 2, |b̅| = 3 and a̅ · b̅ = 2 then find the projection of b̅ on a̅
Answer.

Question. Find the angle between two vectors a̅ and b̅ with magnitudes 1 and 2 respectively and when |a̅ x b̅| = √3
Answer. We have,

Question. Find the projection of a̅ on b̅, if a̅ · b̅ = 8 and b̅ = 2iˆ + 6 jˆ + 3kˆ.
Answer.

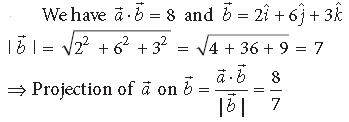
Question. Find the value of p, if (2î+6ĵ+27k̂)x(î+3ĵ+ pk̂) = 0
Answer.

Question.

Answer.

Question. Find a̅ ·b̅, if a̅ =−iˆ + jˆ −2kˆ and b̅ = 2iˆ +3jˆ −kˆ.
Answer.

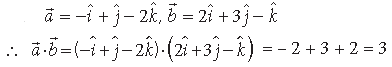
Question. Find the angle between the vectors a̅ = iˆ − jˆ + kˆ and b̅ = iˆ + jˆ − kˆ.
Answer.

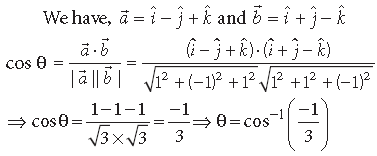
Question.

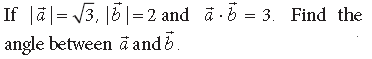
Answer.

Question.

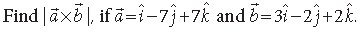
Answer. We have,

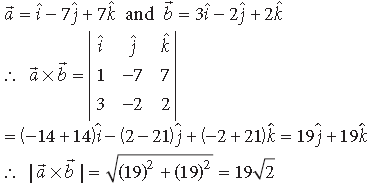
Question. Find the value of the following :
î · ( ĵ x k̂ ) + ĵ · (î x k̂ ) + k̂ · (î x ĵ)
Answer.

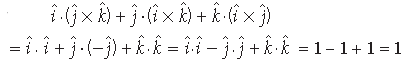
Question, Find the projection of b̅ + c̅ on a̅ where a̅ = iˆ + 2 jˆ + kˆ ,b̅ = iˆ + 3jˆ + kˆ and c̅ = iˆ + kˆ
Answer.

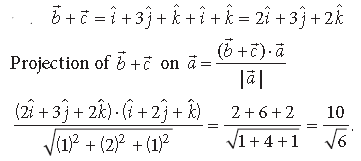
Question.

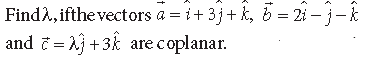
Answer. Since the vectors are coplanar.

⇒ 1(–3 + λ)–3 (6 – 0) + 1(2λ – 0) = 0
⇒ –3 + λ – 18 + 2λ = 0
⇒ 3λ – 21 = 0 ⇒ λ = 7

Question.

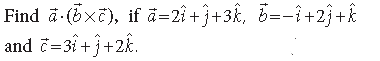
Answer.

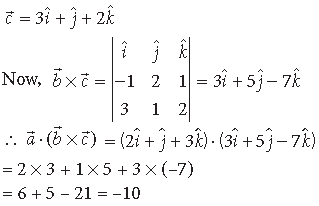
Question. Find the value of λ which makes the

Answer. Since vectors, a̅, b̅, c̅, are coplanar

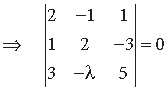
⇒ 2(10 – 3λ) + 1(5+9) + 1(–λ – 6) = 0
⇒ 20 – 6λ + 14 – λ – 6 = 0
⇒ –7λ + 28 = 0 ⇒ λ = 4

Short Answer Type Questions

Question.

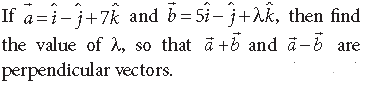
Answer.

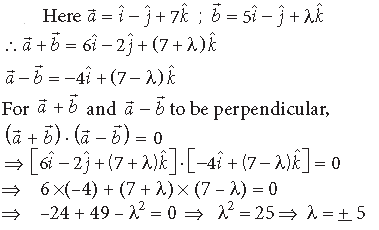
Question. If a̅ b̅ c̅, are three mutually perpendicular vectors of the same magnitude, prove that a̅ + b̅ + c̅, is equally inclined with the vectors a̅, b̅ and c̅
Answer.

Question. Dot product of a vector with vectors iˆ − jˆ + kˆ, 2iˆ + jˆ − 3kˆ and iˆ + jˆ + kˆ are respectively 4, 0 and 2. Find the vector.
Answer. Let the required vector be

Question. Find a vector of magnitude 5 units and perpendicular to each of the vectors (a̅ + b̅) and (a̅ – b̅) where a̅ = iˆ + jˆ + kˆ and b̅ = iˆ + 2 jˆ + 3kˆ
Answer. a̅ = iˆ + jˆ + kˆ and b̅ = iˆ + 2 jˆ + 3kˆ

Question. Show that the vectors a̅, b̅ and c̅ are coplanar if a̅ + b̅, b̅ + c̅ and c̅ + a̅ are coplanar.
Answer. Since, a̅ + b̅, b̅ + c̅ and c̅ + a̅ are coplanar

Question. Find the value of λ so that the four points A, B, C and D with position vectors 4iˆ +5jˆ +kˆ, − jˆ −kˆ , 3iˆ +λjˆ +4k and −4iˆ +4 jˆ +4kˆ respectively are coplanar.
Answer. Here position vectors of A, B, C and D

Question. Find the position vector of a point R which divides the line joining two points P and Q whose position vectors are (2a̅ + b̅) and a̅ + b̅ a̅ − 3b̅  respectively, externally in the ratio 1 : 2. Also, show that P is mid-point of the line segment RQ.
Answer. The position vector of R is given by

Question.

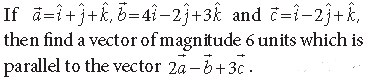
Answer.

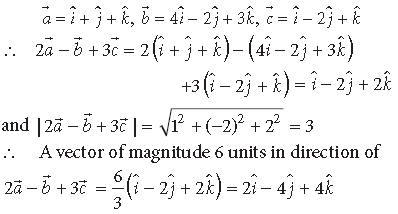
Question. The two adjacent sides of a parallelogram are 2î − 4ĵ − 5k̂ and 2î + 2ĵ + 3k̂ . Find the two unit vectors parallel to its diagonals. Using the diagonal vectors, Find the area of the parallelogram.
Answer. Let a̅ = 2î − 4ĵ − 5k̂ and 2î + 2ĵ + 3k̂

Question.

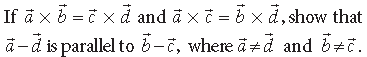
Answer. Two non zero vectors are parallel if and only if their cross product is zero vector.
So, we have to prove that cross product of a̅ − d̅ and b̅ − c̅ is zero vector.

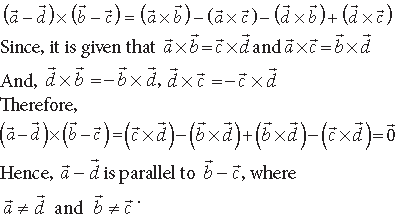
Question. Prove that : [a̅,b̅ + c,d̅][a̅,b̅,d̅] + [a̅,c,d̅].
Answer.

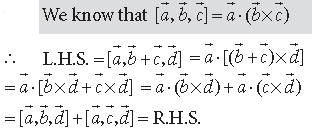
Question. Prove that, for any three vectors a̅ b̅ c̅,

Answer.

Question. Find the values of λ for which the angle between the vectors a̅ = 2λ² iˆ + 4λjˆ + kˆ and b̅ = 7iˆ − 2 jˆ + λkˆ is obtuse.
Answer.

Question. If a̅ ,b̅ and c̅ are three vectors such that each one is perpendicular to the vector obtained by sum of the other two and

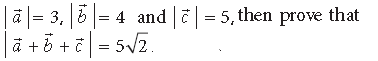
Answer.

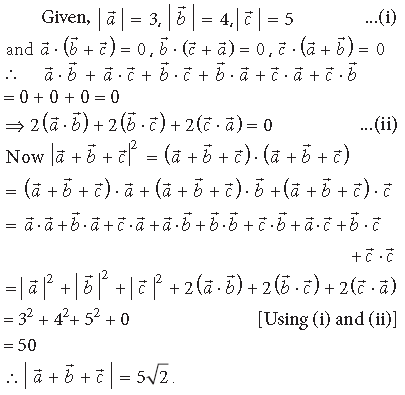
Question.

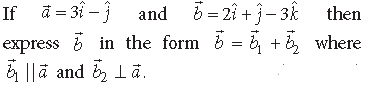
Answer.