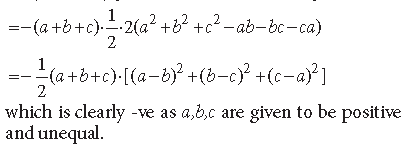Please refer to below Exam Question for Class 12 Mathematics Chapter 4 Determinants. These questions and answers have been prepared by expert Class 12 Mathematics teachers based on the latest NCERT Book for Class 12 Mathematics and examination guidelines issued by CBSE, NCERT, and KVS. We have provided Class 12 Mathematics exam questions for all chapters in your textbooks. You will be able to easily learn problems and solutions which are expected to come in the upcoming class tests and exams for standard 10th.

Chapter 4 Determinants Class 12 Mathematics Exam Question

All questions and answers provided below for Exam Question Class 12 Mathematics Chapter 4 Determinants are very important and should be revised daily.

Exam Question Class 12 Mathematics Chapter 4 Determinants

Very Short Answer Type Questions

Question. Find the maximum value of∴
Answer.

⇒ Δ = 1[(1 + sinθ) (1 + cos θ) – 1]
– 1 (1 + cos θ – 1) +1 (1 – 1 – sin θ)
= 1 + cos θ + sin θ + sin θ cos θ – 1 – cos θ – sin θ
= sin θ cos θ
∴ Maximum value of Δ is 1/2

Question.

Answer.

⇒ (x + 3) (2x) – (–2) (–3x) = 8
⇒ 2x² + 6x – 6x = 8 ⇒ 2x² = 8
⇒ x² = 4 ⇒ x = 2 [x ≠ –2 Q x ∈ N]

Question.

Answer.

⇒ (x + 1)(x + 2) – (x – 3)(x – 1) = 4 × 3 – (1) × (–1)
⇒ x² + x + 2x + 2 – (x² – 3x – x + 3) = 12 + 1
⇒ x² + 3x + 2 – x² +x²– 3 = 13
⇒ 7x = 13 + 1 ⇒ x = 2

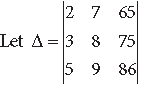
Question.

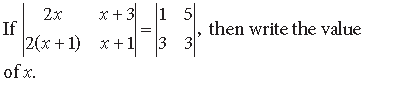
Answer.

⇒ 2x(x + 1) – 2(x + 1) (x + 3) = 3 – 15
⇒ 2x²+ 2x – 2(x² + 4x + 3) = – 12
⇒ 2x²+ 2x – 2x² – 8x – 6 = – 12
⇒ 6x = – 12 + 6 ⇒ x = -6/-6

Question. Evaluate :

Answer.

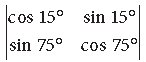
= cos 15° cos75° – sin 75° sin 15°
= cos(15° + 75°) = cos 90° = 0

Question. Evaluate :

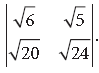
Answer.

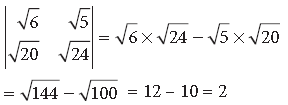
Question. Evaluate :

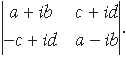
Answer.

= (a + ib) (a – ib) – (c + id) (– c + id)
= (a² + b²) – (– c² – d²)           {∵ i2 = –1}
= a² + b² + c² + d²

Question. Evaluate :

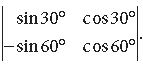
Answer.

= sin30°cos60° + sin60°cos30°.
= sin(30° + 60°) = sin90° = 1

Question. Evaluate :

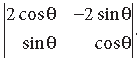
Answer.

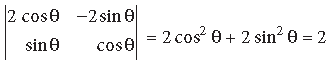
Question.

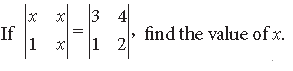
Answer.

⇒ x² – x = 6 – 4 ⇒ x² – x – 2 = 0
⇒ (x – 2) (x + 1) = 0 ⇒ x = 2, x = –1

Question. Write the value of

Answer.

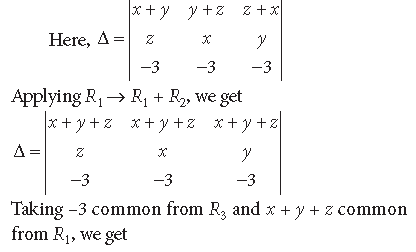
Question. If A is a 3 × 3 matrix, |A| ≠ 0 and |3A| = k |A|, then write the value of k.
Answer. We have, |3A| = k |A|
⇒ 3³ |A| = k |A|
[Using |mA| = mⁿ |A|, where n is order of A]
⇒ k = 27.

Question. Let A be a square matrix of order 3 × 3. Write the value of |2A|, where |A| = 4.
Answer. A is a 3 × 3 matrix and |A| = 4
⇒ |2A| = 2³ · |A| = 8 × 4 = 32.

Question. Write the value of the determinant

Answer. R₁ and R₃ are proportional.
Therefore, value of the determinant is zero.

Question. Show that the following determinant vanishes

Answer.

Question. Without expanding, show that

Answer.

Question.

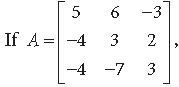
then write the cofactor of the element a₂₁ of its 2^nd row.
Answer.

Question. If A_ij is the cofactor of the element a_ij of the determinant

then write the value of a₃₂ · A_32.

Answer.

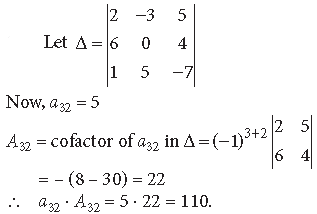
Question.

Answer.

Question.

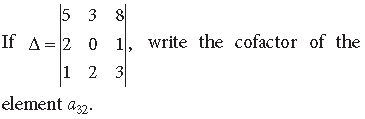
Answer.

Question.

Answer.

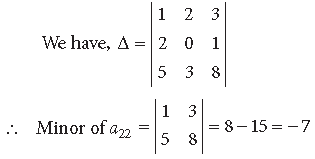
Question. Find the minor of the element of second row and third column (a₂₃) in the determinant

Answer.

Question. If A is a square matrix of order 3 such that |adj A| = 64, find |A|. 
Answer. A is a 3 × 3 matrix s.t. |adj A | = 64.
We know that
|adj A|= |A|^{n – 1}
⇒ 64 = |A|^{3 – 1} ⇒|A|² = 64 ⇒ |A| =± 8.

Question. If A is an invertible square matrix of order 3 and |A| = 5, then find the value of |adj A|.
Answer. Given, |A | = 5 and A is invertible matrix of order 3.
We know that |adj A|= |A|^{n – 1}
⇒ |adj A| = (5)^{3 – 1} ⇒ |adj A| = 25.

Question. For what value of x, is the given matrix

Answer.

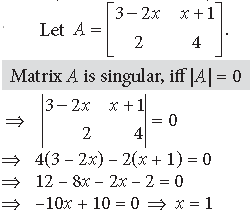
Question. For what value of x, the matrix

is a singular matrix?
Answer.

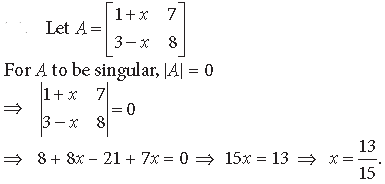
Question. Write A^–1 for

Answer.

Question. For what value of x, the matrix

Answer.

Question.

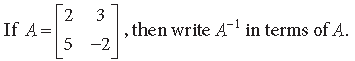
Answer.

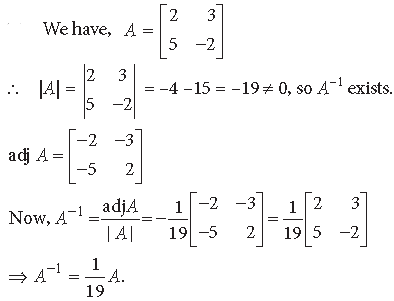
Question. For what value of x is the matrix

Answer.

Question. For what value of x is

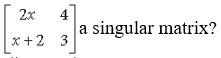
Answer.

⇒ 2(x + 1) (x – 2) – 2x² = 0
⇒ 2(x² – x – 2) – 2x² = 0 ⇒ 2 (– x – 2) = 0
⇒ x = – 2

Question. Write the adjoint of the following matrix :

Answer.

Question.

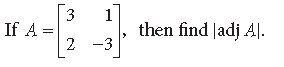
Answer.

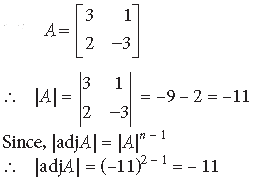
Question. If |A| = 2, where A is a 2 × 2 matrix, find |adj A|.
Answer. |adjA| = |A|^n–1 = (2)^{2– 1} = 2.

Question. If A is a non-singular matrix of order 3 and |adj A| = |A|^k, then write the value of k.
Answer. We know that |adjA| = |A|^{n – 1}
⇒ |adjA| = |A|^{3 – 1} = |A|² = |A|^k
⇒ k= 2

Short Answer Type Questions

Question.

using properties of determinants find the value of f(2x) – f(x).
Answer.

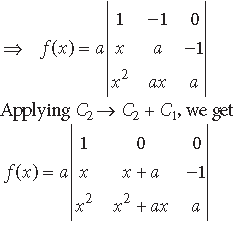
⇒ f(x) = a[a(x + a) + (x² + ax)]
⇒ f(x) = a(a² + ax + ax + x²) = a(a² + 2ax + x²)
Now, f(2x) = a{a² + 2a (2x) + (2x)²} = a(a² + 4ax + 4x²)
∴ f(2x) – f(x) = a( a² + 4ax + 4x² – a² – 2ax – x²)
= ax(3x + 2a)

Question. Using properties of determinants, prove the following :

Answer.

Question. Using properties of determinants, prove the following

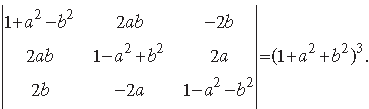
Answer.

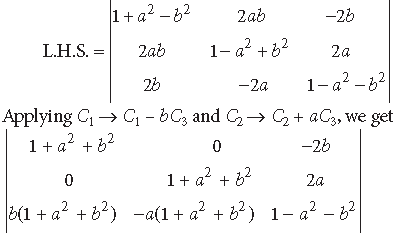
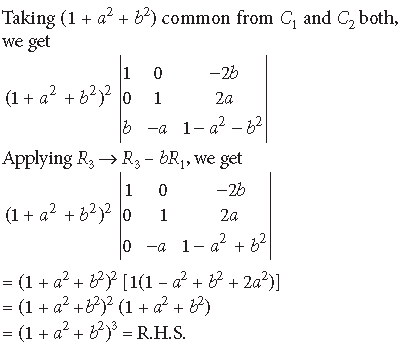
Question. Using properties of determinants, prove the following :

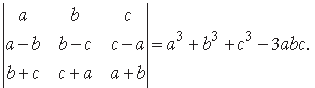
Answer.

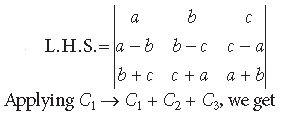
Question. Using properties of determinants, prove the following :

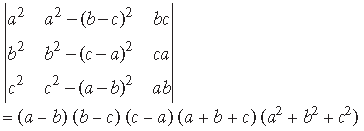
Answer.

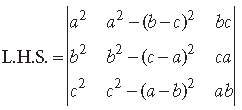
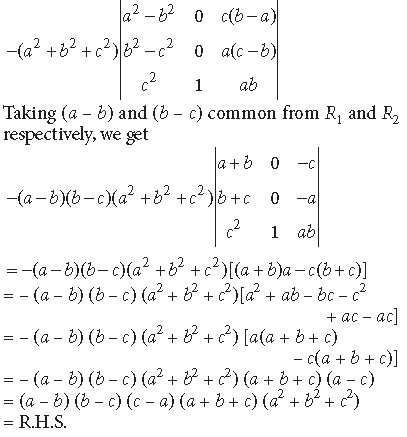
Question. Using properties of determinants, prove the following :

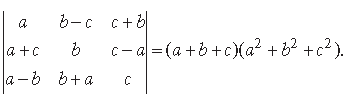
Answer.

Question. Using properties of determinants, prove the following

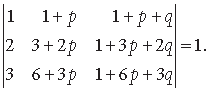
Answer.

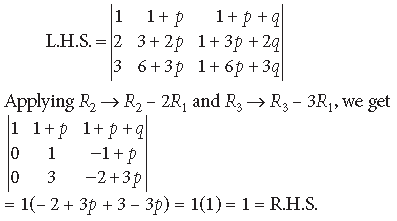
Question.

Answer.

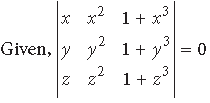
Since each element of third column of determinant is the sum of two elements, therefore determinants can be expressed as the sum of two determinants given by

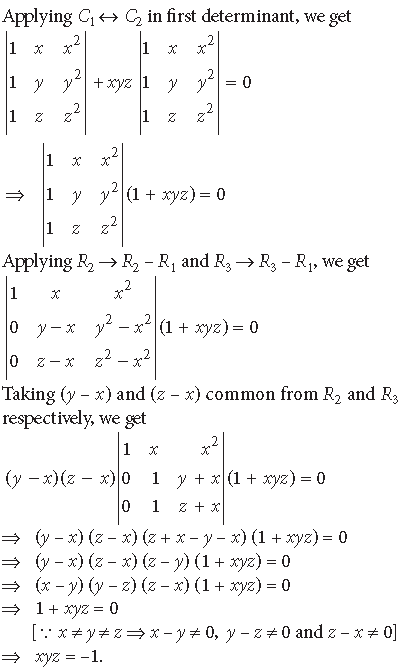
Question. Using properties of determinants, prove the following:

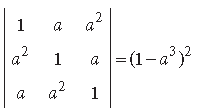
Answer.

Question. Using properties of determinants, prove that

Answer.

Question. Using properties of determinants, solve for x :

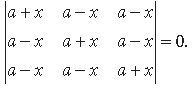
Answer.

Question. Using properties of determinants, prove that

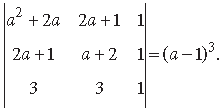
Answer.

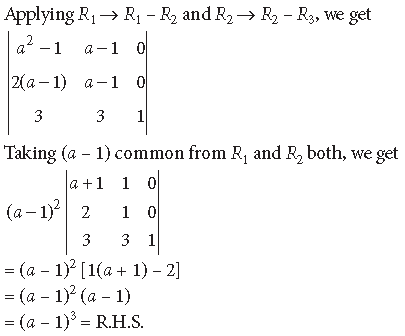
Question. Find the equation of the line joining A(1, 3) and B(0, 0) using determinants and find the value of k if D(k, 0) is a point such that area of ΔABD is 3 square units.
Answer. Using determinants, the line joining A(1, 3)

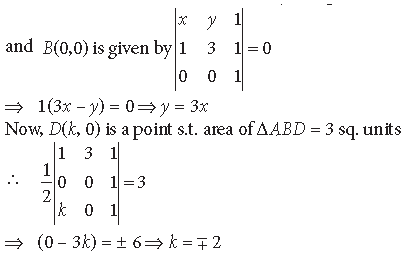
Question.

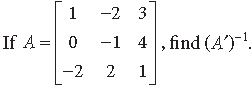
Answer.

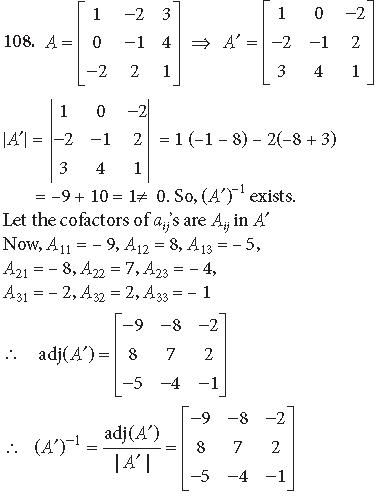
Question. Find the adjoint of the matrix

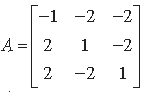
and hence show that A·(adj A) = |A|I₃.
Answer.

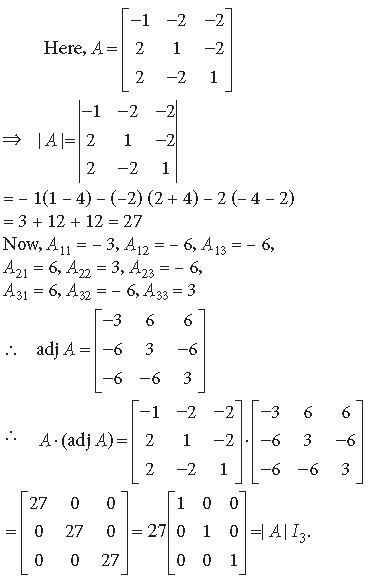
Question. Using properties of determinants, prove that

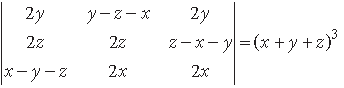
Answer.

Question. Prove the following using properties of determinants :

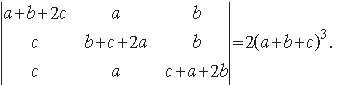
Answer.

Question. Using properties of determinants, prove the following:

Answer.

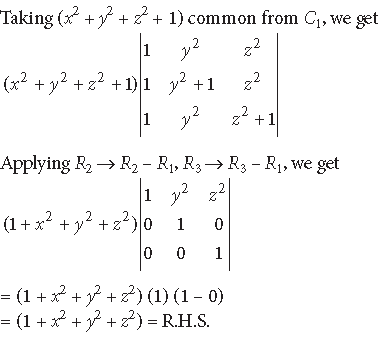
Question. Using properties of determinants, prove the following :

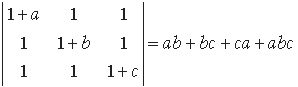
Answer.

Question. Using properties of determinants, prove that

Answer.

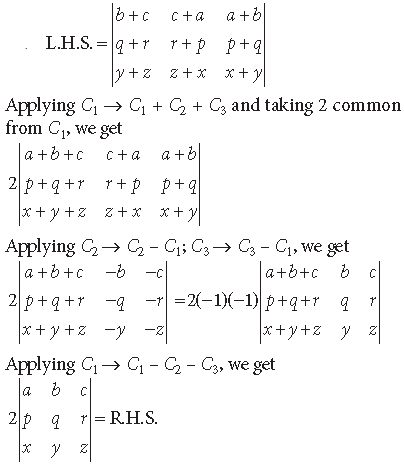
Question. Find the inverse of the matrix

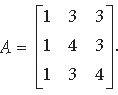
112.

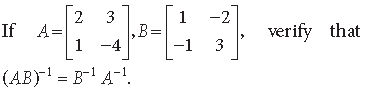
Answer.

Question. Show that the matrix

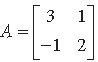
satisfies the equation A² – 5A + 7I = O. Hence, find A^–1.
Answer.

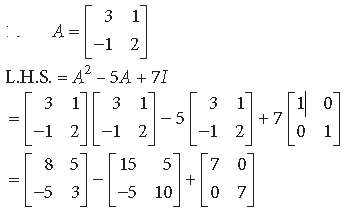
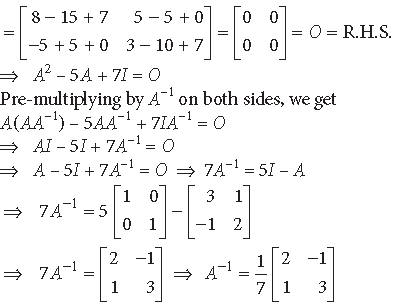
Question. The monthly incomes of Aryan and Babban are in the ratio 3 : 4 and their monthly expenditures are in the ratio 5 : 7. If each saves ₹ 15,000 per month, find their monthly incomes using matrix method. This problem reflects which value? 
Answer. Let the monthly income of Aryan be ₹ 3x and that of Babban be ₹ 4x
Also, let monthly expenditure of Aryan be ₹ 5y and
that of Babban be ₹ 7y
According to question,
3x – 5y = 15000
4x – 7y = 15000
These equations can be written as
AX = B

⇒ x = 30000 and y = 15000
So, monthly income of Aryan = 3 × 30000 = `90000
Monthly income of Babban = 4 × 30000 = `120000
From this question we are encouraged to save a part of money every month.

Question. Using properties of determinants, show that

Answer.

Since each element in the first column of determinant is the sum of two elements, therefore, determinant can be expressed as the sum of two determinants given by

Taking x common from R₁, R₂, R₃ in first determinant and x common from C₂, C₃, y common from C₁ in second determinant, we get

Question. Using properties of determinants, prove that :

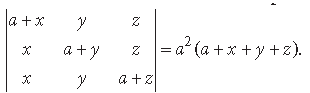
Answer.

Question. Using properties of determinants, prove that :

Answer.

Question. Using properties of determinants, prove the following :

Answer.

Long Answer Type Questions

Question. Using properties of determinants, show that ΔABC is isosceles, if

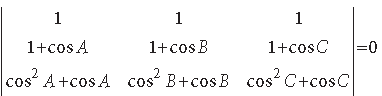
Answer. We have,

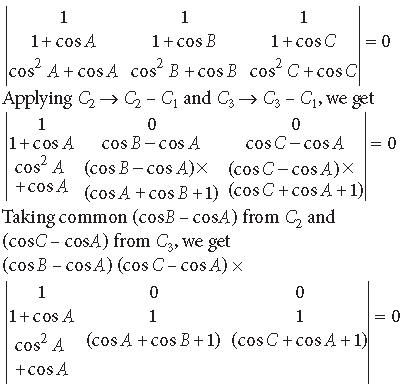
⇒ (cos B – cos A) (cos C – cos A) (cos C – cos B) = 0
⇒ cos B = cos A ⇒ B = A
or cos C = cos A ⇒ C = A or cosC = cosB ⇒ C = B
∴ ΔABC is an isosceles triangle.

Question. If a, b and c are all non-zero and

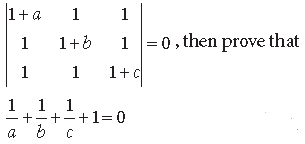
Answer.

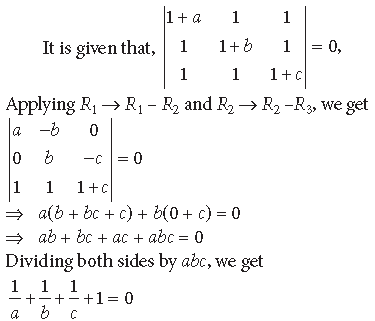
Question. Two schools P and Q want to award their selected students on the values of discipline, politeness and punctuality. The school P wants to award ₹ x each, ₹ y each and ₹ z each for the three respective values to its 3, 2 and 1 students with a total award money of ₹ 1,000. School Q wants to spend ₹ 1,500 to award its 4, 1 and 3 students on the respective values (by giving the same award money for the three values as before). If the total amount of awards for one prize on each value is ₹ 600, using matrices, find the award money for each value. Apart from the above three values, suggest one more value for awards.
Answer. According to question, we have,
3x + 2y + z = 1000          …(i)
4x + y + 3z = 1500         …(ii)
x + y + z = 600              …(iii)
The given system of equations can be written as AX = B

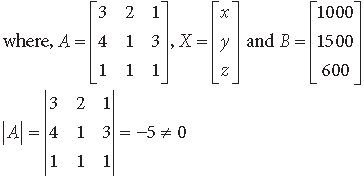
∴ A is invertible and system of equations has a unique solution given by X = A^–1 B
Now, A₁₁ = –2, A₁₂ = –1, A₁₃ = 3,
A₂₁ = –1, A₂₂ = 2, A₂₃ = –1,
A₃₁ = 5, A₃₂ = –5, A₃₃ = –5

⇒ x = 100, y = 200, z = 300
Hence the money awarded for discipline, politeness and punctuality are ₹ 100, ₹ 200 and ₹ 300 respectively.
Apart from the above three values schools can award children for sincerity.

Question. A total amount of ₹ 7,000 is deposited in three different savings bank accounts with annual interest rates of 5%, 8% and 8(1/2)% respectively. The total annual interest from these three accounts is ₹ 550. Equal amounts have been deposited in the 5% and 8% savings accounts. Find the amount deposited in each of the three accounts, with the help of matrices.
Answer. Let x, y and ` z be deposited at the rates of interest 5%, 8% and 8(1/2)% respectively.
According to question,
x + y + z = 7000
x – y = 0

∴ A^–1 exists. So, system of equations has a unique solution and it is given by X = A^–1B
Now, A₁₁ = –17, A₁₂ = –17, A₁₃ = 26,
A₂₁ = –1, A₂₂ = 7, A₂₃ = –6,
A₃₁ = 1, A₃₂ = 1, A₃₃ = –2

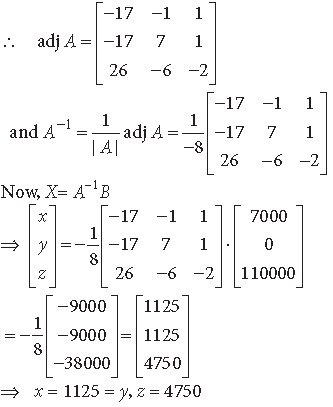
Question. Using matrices, solve the following system of linear equations :
x – y + 2z = 7, 3x + 4y – 5z = – 5
2x – y + 3z = 12
Answer. We have,
x – y + 2z = 7
3x + 4y – 5z = – 5
2x – y + 3z = 12
The given system of equations can be written as
AX = B

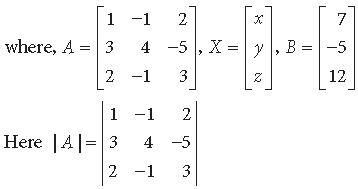
= 1 (12 – 5) – 3(– 3 + 2) + 2(5 – 8)
= 7 + 3 – 6 = 4 􀁺 0.
∴ A^–1 exists. So, system of equations has a unique
solution given by X = A–1B
Now, A₁₁ = 7, A₁₂ = –19, A₁₃ = – 11, A₂₁ = 1, A₂₂ = –1,
A₂₃ = –1, A₃₁ = –3, A₃₂ = 11, A₃₃ = 7

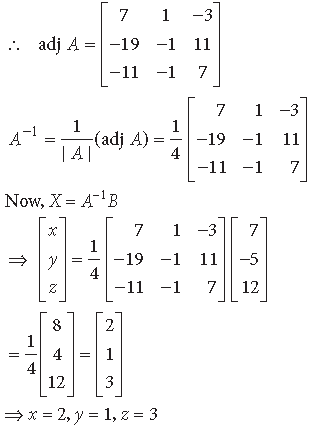
Question. Using matrices, solve the following system of equations :
2x + 3y + 3z = 5, x – 2y + z = – 4,
3x – y – 2z = 3
Answer. We have,
2x + 3y + 3z = 5
x – 2y + z =- 4
3x – y – 3z = 3
The given system of equations can be written as AX = B

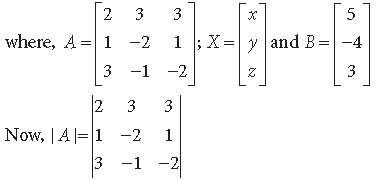
= 2(4 + 1) – 3(– 2 – 3) + 3(– 1 + 6)
= 10 + 15 + 15 = 40 ≠ 0
∴ A^–1 exists. So, system of equations has a unique solution and it is given by X = A^–1B
Now, A₁₁ = 5, A₁₂ = 5, A₁₃ = 5, A₂₁ = 3, A₂₂ = –13,
A₂₃ = 11, A₃₁ = 9, A₃₂ = 1, A₃₃ = –7

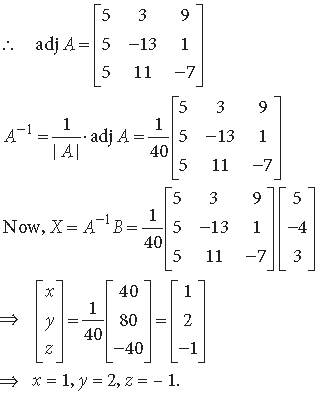
Question. Using matrices, solve the following system of equations :
3x + 4y + 7z = 4; 2x – y + 3z = – 3;
x + 2y – 3z = 8
Answer. We, have
3x + 4y + 7z = 4
2x – y + 3z = – 3
3x + 2y – 3z = 8
The system of equations can be written as AX = B

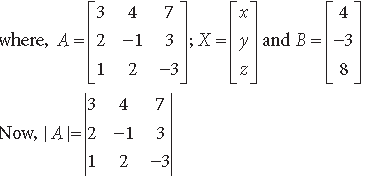
= 3(3 – 6) – 4(– 6 – 3) + 7(4 + 1)
= – 9 + 36 + 35 = 62 ≠ 0
∴ A^–1 exists. So, system of equations has a unique
solution given by X = A^–1B
Now, A₁₁ = –3, A₁₂ = 9, A₁₃ = 5, A₂₁ = 26, A₂₂ = –16,
A₂₃ = –2, A₃₁ = 19, A₃₂ = 5, A₃₃ = –11

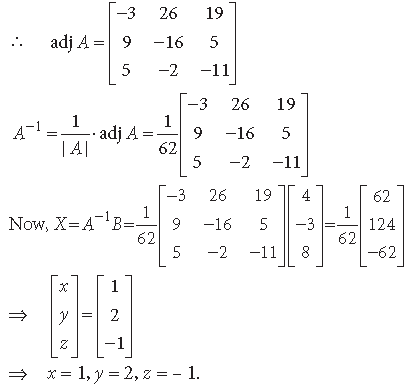
Question. Two schools, P and Q, want to award their selected students for the values of sincerity, truthfulness and hard work at the rate of ₹ x, ₹ y and ₹ z for each respective value per student. School P awards its 2, 3 and 4 students on the above respective values with a total prize money of ₹ 4,600. School Q wants to award its 3, 2 and 3 students on the respective values with a total award money of ₹ 4,100. If the total amount of award money for one prize on each value is ₹ 1,500, using matrices find the award money for each value. Suggest one other value which the school can consider for awarding the students. 
Answer. According to question, we have
x + y + z = 1500
2x + 3y + 4z = 4600
3x + 2y + 3z = 4100
The system of equations can be written as AX = B

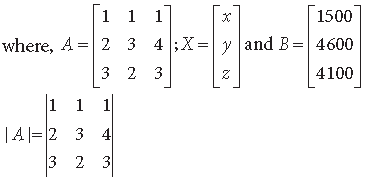
= 1(9 – 8) – 1(6 – 12) + 1(4 – 9)
= 1 + 6 – 5 = 2 􀁺􀀃0
∴ A^–1 exists and so, system of equations has a
unique solution given by X = A^–1B
Now, A₁₁ = 1, A₁₂ = 6, A₁₃ = –5,
A₂₁ = –1, A₂₂ = 0, A₂₃ = 1,
A₃₁ = 1, A₃₂ = –2, A₃₃ = 1

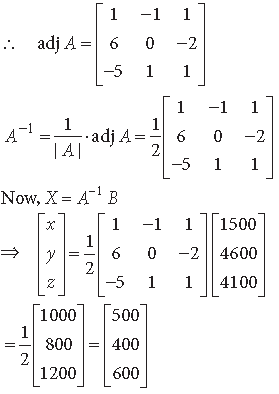
⇒ x = 500; y = 400; z = 600.
Apart from sincerity, truthfulness and hard work,
the schools can include an award for regularity.

Question. If a, b, c are positive and unequal, show that the following determinant is negative.

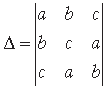
Answer.

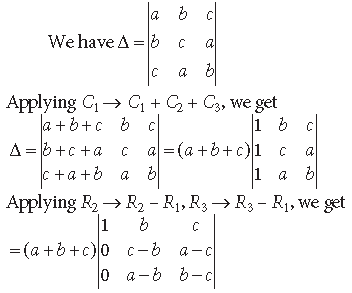
= (a + b + c) [(c – b) (b – c) – (a – b) (a – c)]
= (a + b + c) [(bc – c² – b²+ bc ) – (a² – ac – ab + bc)]
= (a + b + c) [2bc – c² – b² – a² + ac + ab – bc]
= (a + b + c) [–a² – b² – c² + ab + bc +ca]
= –(a + b + c) [a² + b² + c² – ab – bc – ca]