MCQs for Mathematics Class 11 with Answers Chapter 10 Straight Lines
Students of class 11 Mathematics should refer to MCQ Questions Class 11 Mathematics Straight Lines with answers provided here which is an important chapter in Class 11 Mathematics NCERT textbook. These MCQ for Class 11 Mathematics with Answers have been prepared based on the latest CBSE and NCERT syllabus and examination guidelines for Class 11 Mathematics. The following MCQs can help you to practice and get better marks in the upcoming class 11 Mathematics examination
Chapter 10 Straight Lines MCQ with Answers Class 11 Mathematics
MCQ Questions Class 11 Mathematics Straight Lines with answers provided below have been prepared by expert teachers of grade 11. These objective questions with solutions are expected to come in the upcoming Standard 11 examinations. Learn the below provided MCQ questions to get better marks in examinations.
Question. The point on X-axis which is equidistant from the points (3, 2) and (−5, − 2) is
(a) (1, 0)
(b) (2, 0)
(c) (−1,0)
(d) (−2,0)
Answer
C
Question. The equation of line, which passes through point (4, 3) and parallel to the line 2x − 3y = 7 is
(a) 2x − 3y + 1 =0
(b) 2x − 3y −1 =0
(c) 2x + 3y + 1 =0
(d) 2x + 3y −1 =0
Answer
A
Question. The angle between the X -axis and the line joining the points (3, − 1) and (4, − 2) is
(a) 45°
(b) 135°
(c) 90°
(d) 180°
Answer
B
Question. The point (− 3, 2) is located in the quadrant
(a) quadrant I
(b) quadrant II
(c) quadrant III
(d) quadrant IV
Answer
B
Question. The tangent of angle between the lines whose intercepts on the axes are a, −b and b, −a respectively, is
(a) a2-b2 /ab
(b) b2-a2/2
(c) b2-a2/2ab
(d) None of these
Answer
B
Question. Lines through the points (−2, 6) and (4, 8) is perpendicular to the line through the points (8, 12) and (x, 24). Then, the value of x is
(a) 2
(b) 6
(c) 8
(d) 4
Answer
D
Question. The coordinates of a point which divides the line segment joining A (1, − 3) and B (− 3, 9) internally in the ratio 1 : 3, are given by
(a) (−2, 6)
(b) (0,0)
(c) (-6/4, 18/4)
(d) (10/4 ,-30/4)
Answer
B
Question. The equations of the line which have slope 1/2 and cuts-off an intercept 4 on X -axis is
(a) x −2y −4 =0
(b) x + 2y −4 =0
(c) x + 2y + 4 =0
(d) x −2y + 4 =0
Answer
A
Question. If the vertices of a triangle are P (1, 3),Q (2, 5) and R(3, − 5), then the centroid of a DPQR is
(a) (1, 2)
(b) (1, 3)
(c) (3, 1)
(d) (2, 1)
Answer
D
Question. The points (1, − 1), (5, 2) and (9, 5) collinear.
(a) Yes
(b) No
(c) Cannot say
(d) Insufficient information
Answer
A
Question. Area of the triangle whose vertices are (4, 4), (3, −2) and (− 3, 16), is
(a) 54
(b) 27
(c) 53
(d) 106
Answer
B
Question. The equation of the line through (− 2, 3) with slope − 4 is
(a) x + 4y −10 =0
(b)4x + y + 5 =0
(c) x + y −1 =0
(d) 3x + 4y − 6 =0
Answer
B
Question. The equation of the line passing through the point (1, 2) and perpendicular to the line x + y + 1 = 0 is
(a) y − x + 1 =0
(b) y − x −1 =0
(c) y − x + 2 =0
(d) y − x −2 =0
Answer
B
Question. The slope of line, whose inclination is 60°, is
(a) 1/√3
(b) 1
(c) √3
(d) Not defined
Answer
C
Question. The value of y is, if the distance between points P (2, − 3) andQ (10, y ) is 10 units.
(a) 3
(b) 9
(c) − 3
(d) None of these
Answer
A
Question. The slope of that line, which passes through the points (at 22 , 2at2) and (at22, 2at2) is
(a) 2/t2 – t1
(b) 2/t2 + 2t1
(c) 1/t2 – t1
(d) 2/t2 + t1
Answer
D
Question. The distance of the point of intersection of the lines 2x − 3y + 5 = 0 and 3x + 4y = 0 from the line 5x − 2y = 0 is
(a) 130/17 29
(b) 13/7 29
(c) 130/7
(d) None of these
Answer
A
Question. The angle between the lines
y =(2 −√3)(x +5) and y = (2 + √3)(x − 7) is
(a) 30°
(b) 90°
(c) 45°
(d) 120°
Answer
D
Question. The value of y will be, so that the line through (3, y ) and (2, 7) is parallel to the line through (−1, 4) and (0, 6).
(a) 7
(b) 8
(c) 9
(d) 10
Answer
C
Question. If the normal form of the equation √3x + y − 8 = 0 is x cos w + y sin w = p, then p and w respectively are
(a) 4, 45°
(b) 4, 30°
(c) 3, 45°
(d) 3, 30°
Answer
B
Question. The slope of a line whose inclination is 90°, is
(a) 1
(b) 0
(c) −1
(d) not defined
Answer
D
Question. Using slope of line, till, are A(4, 4), B(3, 5) andC(−1, 1) the vertices of a right angled triangle.
(a) Yes
(b) No
(c) Cannot say
(d) Insufficient Information
Answer
A
Question. The points A (x, 4), B (3, − 2) and C (4, − 5) are collinear in the value of x is
(a) 1
(b) 2
(c) −1
(d) 0
Answer
A
Question. The equation of the lines parallel to the X-axis and passing through the point (− 3, 5) is
(a) x = − 3
(b) y = − 3
(c) x =5
(d) y =5
Answer
D
Question. The equation of a line perpendicular to the line x − 2y + 3 = 0 and passing through the point (1, – 2) is
(a) y =2x
(b) x =2y
(c) x = −2y
(d) y = −2x
Answer
D
Question. A line cutting off intercept −3 from the Y-axis and the tangent at angle to the X-axis is 3/5 , its equation is
(a) 5y − 3x + 15 =0
(b) 3y −5x + 15 =0
(c) 5y − 3x −15 =0
(d) None of these
Answer
A
Question. The coordinates of a point which divides externally the line joining (1, −3) and (− 3, 9) in the ratio 1 : 3 are
(a) (3, − 6)
(b) (− 6, 3)
(c) (3, −9)
(d) (−9, 3)
Answer
C
Question. Slope of a line which cuts off intercepts of equal lengths on the axes is
(a) −1
(b)0
(c) 2
(d) 3
Answer
A
Question. If the line x/a + y/b= 1passes through the points (2, −3) and (4, −5), then (a, b) is
(a) (1, 1)
(b) (−1, 1)
(c) (1, −1 )
(d) (−1, −1 )
Answer
D
Question. If the coordinates of the middle point of the portion of a line intercepted between the coordinate axes is (3, 2), then the equation of the line will be
(a)2x + 3y =12
(b) 3x + 2y =12
(c)4x − 3y = 6
(d) 5x −2y =10
Answer
A
Question. Transform the equation of the line 3x + 2y − 7 = 0 to slope intercept form then the slope and y-intercept will be
(a) 3/2 , 7/2
(b) -3/2,-7/2
(c) -3/2, 7/2
(d) None of these
Answer
C
Question. Transform the equation of the line 3x + 2y − 7 = 0 to normal form then the inclination of the perpendicular segment from the origin on the line with the axis and its length is
(a) tan-1 (1/3).7/√13
(b) tan-1 (2/3).7/√13
(c) tan-1 (3/4).7/√13
(d) tan-1 (1/5).7/√13
Answer
B
Question. The line passing through the points (− 4, 5) and (− 5, 7) also passes through the point (l , m), then 2l + m + 3 is equal to
(a) 1
(b) −1
(c) 2
(d) 0
Answer
D
Question. The angle between the lines
y − √3x − 5 = 0 and √3y − x + 6 = 0 will not be
(a) 30°
(b) 150°
(c) 45°
(d) None of these
Answer
C
Question. The angle between the lines
x − 2y + 3 = 0 and 3x + y − 1 = 0 is
(a) − tan−1 ( 7)
(b) tan−1(1/7)
(c) π − tan−1 (7)
(d) 2π − tan−1 (7)
Answer
C
Question. The distance of the point (3, − 5) from the line 3x − 4y − 26 = 0 is
(a) 3/7
(b) 2/5
(c) 7/5
(d) 3/5
Answer
D
Question. The perpendicular distance from origin to the line 5x + 12y − 13 = 0 is
(a) 10 unit
(b) 5 unit
(c) 2 unit
(d) 1 unit
Answer
D
Question. The distance between the parallel lines
3x − 4y + 7 = 0 and 3x − 4y + 5 = 0, is
(a) 3/7
(b) 7/5
(c) 2/5
(d) 3/5
Answer
C
Question. The equation of line passing through the points (−1, 1) and (2, − 4).
(a) 5x + 2y + 2 =0
(b) 5x + 3y −2 =0
(c) 5x + 2y + 3 =0
(d) 5x + 3y + 2 =0
Answer
D
Question. The distance between the lines 3x + 4y = 9 and 6x + 8y = 15 is
(a) 3/10
(b) 2/25
(c) 7/10
(d) 3/25
Answer
A
Question. Population vs Year graph given below.
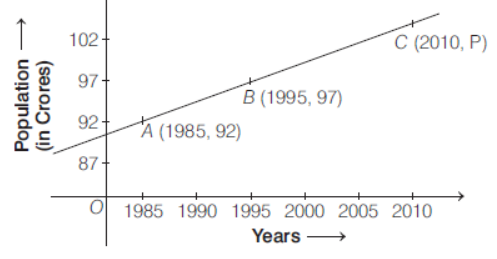
Based on the above information answer the following questions.
(i) The slope of line AB is
(a) 2
(b) 1
(c) 1/2
(d) 1/3
Answer
C
(ii) The equation of line AB is
(a) x + 2y =1791
(b) x −2y =1801
(c) x −2y =1791
(d) x −2y + 1801 =0
Answer
B
(iii) The population in year 2010 is
(in crores)
(a) 104.5
(b) 119.5
(c) 109.5
(d) None of these
Answer
A
(iv) The equation of line perpendicular to line AB and passing through (1995, 97) is
(a) 2x − y =4087
(b) 2x + y =4087
(c) 2x + y =1801
(d) None of the above
Answer
B
(v) In which year the population becomes 110 crores is
(a) 2020
(b) 2019
(c) 2021
(d) 2022
Answer
C
Question. Three girls, Rani, Mansi, Sneha are talking to each other while maintaining a social distance due to covid-19. They are standing on vertices of a triangle, whose coordinates are given.
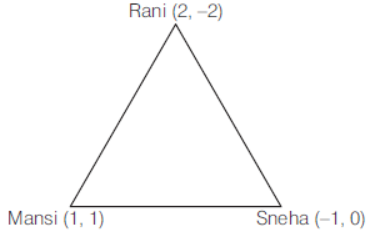
Based on the above information answer the following questions.
(i) The equation of lines formed by Rani and Mansi is
(a) 3x − y =4
(b) 3x + y =4
(c) x − 3y =4
(d) x + 3y =4
Answer
B
(ii) Slope of equation of line formed by Rani and Sneha is
(a) 2/3
(b) − 3/2
(c)−2/3
(d) 1/3
Answer
C
(iii) The equation of median of lines through Rani is
(a) 5x + 4y =2
(b) 5x −4y =2
(c) 4x −5y =1
(d) None of these
Answer
A
(iv) The equation of altitude through Mansi is
(a) 3x −2y =1
(b) 2x + 3y =5
(c) x + 2y = 3
(d) None of these
Answer
A
(v) The equation of line passing through the Rani and parallel to line formed by Mansi and Sneha is
(a) x −2y =4
(b) x + 2y = 6
(c) x −2y = 6
(d) 2x + y =4
Answer
C

We hope the above MCQ Questions Class 11 Mathematics Straight Lines with answers based on the latest syllabus and examination guidelines issued by CBSE, NCERT and KVS are really useful for you. Straight Lines is an important chapter in Class 11 as it provides very strong understanding about this topic. Students should go through the answers provided for the MCQs after they have themselves solved the questions. All MCQs have been provided with four options for the students to solve. These questions are really useful for benefits of class 11 students. Please go through these and let us know if you have any feedback in the comments section.
