MCQs for Mathematics Class 11 with Answers Chapter 4 Principle of Mathematical Induction
Students of class 11 Mathematics should refer to MCQ Questions Class 11 Mathematics Principle of Mathematical Induction with answers provided here which is an important chapter in Class 11 Mathematics NCERT textbook. These MCQ for Class 11 Mathematics with Answers have been prepared based on the latest CBSE and NCERT syllabus and examination guidelines for Class 11 Mathematics. The following MCQs can help you to practice and get better marks in the upcoming class 11 Mathematics examination
Chapter 4 Principle of Mathematical Induction MCQ with Answers Class 11 Mathematics
MCQ Questions Class 11 Mathematics Principle of Mathematical Induction with answers provided below have been prepared by expert teachers of grade 11. These objective questions with solutions are expected to come in the upcoming Standard 11 examinations. Learn the below provided MCQ questions to get better marks in examinations.
Question: The value of (1+3/1)(1+5/4)(1+7/9)…(1+2n+1/n2) is
(a) (n + 1)
(b) n + 1)2
(c) 2(n+1)2
(d) None of these
Answer
D
Question: If P (n) is a statement (n∈ N ) such that, if P (k) is true, P (k +1) is true for k ∈ N , then P (n) is true
(a) for all n
(b) for all n > 1
(c) for all n > 2
(d) Nothing can be said
Answer
C
Question: For all n ∈ N ,n (n+1 )(n+5 ) is a multiple of
(a) 4
(b) 3
(c) 5
(d) 7
Answer
A
Question: For n∈ N,(1/5)n5+(1/3)n3+(7/15)n is
(a) an integer
(b) a natural number
(c) a positive fraction
(d) None of these
Answer
B
Question: If P (n ) is a statement such that P(3) is true.
Assuming P(k) is true⇒ p (k+1) is true for all k ≥ 3, then P (n) is true
(a) for all n
(b) for n≥ 3
(c) for n > 4
(d) None of these
Answer
B
Question:
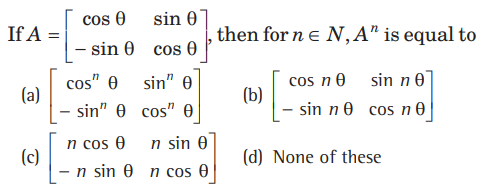
Answer
B
Question: The smallest positive integer n for which n!<(n+1/2)n holds, is
(a) 1
(b) 2
(c) 3
(d) 4
Answer
B
Question: Let P (n): n2+n+1 is an even integer. If P(k) is assumed true ⇒p(k+1) is true. Therefore, P (n) is true
(a) for n > 1
(b) for all n ∈ N
(c) for n > 2
(d) None of these
Answer
B
Question:
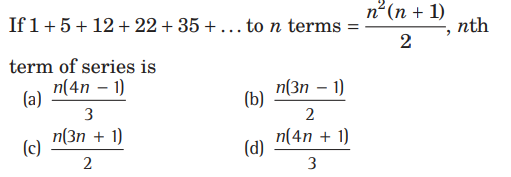
Answer
B
Question: The inequality n !>2n-1 is true for
(a) n > 2
(b) n∈ N
(c) n > 3
(d) None of these
Answer
A
Question: The greatest positive integer, which divides (n+2 )( n+3) (n+4 )(n+5) (n+6) for all n ∈N, is
(a) 4
(b) 120
(c) 240
(d) 24
Answer
B
Question:
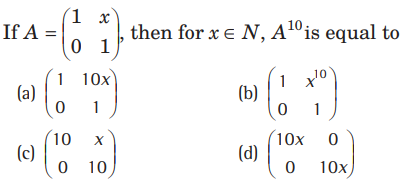
Answer
A
Question: If xn-1 is divisible by x-k, then the least positive integral value of k is
(a) 1
(b) 2
(c) 3
(d) 4
Answer
A
Question: For all n ∈ N,3.52n+1 +23n+1 is divisible by
(a) 19
(b) 17
(c) 23
(d) 25
Answer
B
Question: If m, n are any two odd positive integer with n< m,then the largest positive integers which divides all the numbers of the type m2 -n2 is
(a) 4
(b) 6
(c) 8
(d) 9
Answer
C
Question: For all n ∈ N, 2.42n+1+ 33n+1 is divisible by
(a) 2
(b) 9
(c) 3
(d) 11
Answer
D
Question: 23n– 7n- 1 is divisible by
(a) 64
(b) 36
(c) 49
(d) 25
Answer
C
Question: If x2n-1 +y2n-1 is divisible by x+ y, if n is
(a) a positive integer
(b) an even positive integer
(c) an odd positive integer
(d) None of these
Answer
A
Question: For all n ∈ N,41n -14n is a multiple of
(a) 26
(b) 27
(c) 25
(d) None of these
Answer
B
Question: For each n ∈ N ,102n-1 +1 is divisible by
(a) 11
(b) 13
(c) 9
(d) None of these
Answer
A
Question: x(xn-1 -nα n-1)+ αn(n-1) is divisible by (x-α)2 for
(a) n > 1
(b) n > 2
(c) all n ∈ N
(d) None of the above
Answer
C
Question: For each n ∈ N, 32n-1 is divisible by
(a) 8
(b) 16
(c) 32
(d) None of these
Answer
A
Question: If 49n + 16n + k is divisible by 64 for n ∈ N, then the least negative integral value of k is
(a) –1
(b) –2
(c) –3
(d) –4
Answer
A
Question: If n ∈ N, then 11n+2 +122n+1 is divisible by
(a) 113
(b) 123
(c) 133
(d) None of these
Answer
C
Question: For a positive integer n,let a(n) =1+1/2+1/3+1/4+…+1/n. Then,
(a) a (100) ≤ 100
(b) a (100) >100
(c) a (200) ≤ 100
(d) None of these
Answer
A
Question: For all positive integral values ofn,32n -2n+1 is divisible by
(a) 2
(b) 4
(c) 8
(d) 12
Answer
A
Question: 10n +3(4n+2)+5 is divisible by (n ∈ N)
(a) 7
(b) 5
(c) 9
(d) 17
Answer
C
Question: For natural number n,2n(n-1)! <n ,if
(a) n < 2
(b) n > 2
(c) n≥ 2
(d) never
Answer
B
We hope the above MCQ Questions Class 11 Mathematics Principle of Mathematical Induction with answers based on the latest syllabus and examination guidelines issued by CBSE, NCERT and KVS are really useful for you. Principle of Mathematical Induction is an important chapter in Class 11 as it provides very strong understanding about this topic. Students should go through the answers provided for the MCQs after they have themselves solved the questions. All MCQs have been provided with four options for the students to solve. These questions are really useful for benefit of class 11 students. Please go through these and let us know if you have any feedback in the comments section
