Students of class 11 Mathematics should refer to MCQ Questions Class 11 Mathematics Trigonometric Functions with answers provided here which is an important chapter in Class 11 Mathematics NCERT textbook. These MCQ for Class 11 Mathematics with Answers have been prepared based on the latest CBSE and NCERT syllabus and examination guidelines for Class 11 Mathematics. The following MCQs can help you to practice and get better marks in the upcoming class 11 Mathematics examination

Chapter 3 Trigonometric Functions MCQ with Answers Class 11 Mathematics

MCQ Questions Class 11 Mathematics Trigonometric Functions with answers provided below have been prepared by expert teachers of grade 11. These objective questions with solutions are expected to come in the upcoming Standard 11 examinations. Learn the below provided MCQ questions to get better marks in examinations.

Question. If in a DABC, 3 a = b + c, then cot B/2 cot C/2 is equal to
(a) 1
(b) √3
(c) 2
(d) None of these

Question:

(a) √13√
(b) √14
(c) √17
(d) √15 

Question: The value of sin 36° sin 72° sin108° sin 144°  is equal to
(a) 1/4
(b) 1/16
(c) 3/4
(d) 5/16 

Question: If tan x= b/a,  then find the value of √a+b/a-b +√a-b/a+b·
(a) 2cos x/√cos2x
(b) cos x/√cos 2x
(c) 2 cos 2x/√cos x
(d) None of these 

Question: If A = sin2  θ + cos4 θ, 2 then for all real values of θ
(a) 1 ≤ A ≤ A
(b) 3/4 ≤ A ≤ 1
(c) 13/16 ≤ A≤1
(d) 3/4 ≤ A≤13/16 

Question:

Question: If sinθ  +cosθ = x, then sin⁶ θ +cos⁶ θ=1/4[4-3(x²-1)²]  for
(a) all real x
(b) x² ≤ 2
(c) x²>2
(d) None of these 

Question: If sin θ =√3cos θ,-π<θ <0,  then θ is equal to
(a) -5π/6
(b) -4π/6
(c) 4π/6
(d) 5π/6 

Question: The value of 2cos x – cos 3x- cos 5x  is equal to
(a) 16 cos³ x sin² x
(b) 16 sin³ x cos²x 
(c) 4 cos³x sin² x 
(d) 4sin³ xcos² x 

Question: Consider the following statements :

Which of the statements given above is/are correct ?
(a) Only (I)
(b) Only (II)
(c) Both (I) and (II)
(d) Neither (I) nor (II)

Question:

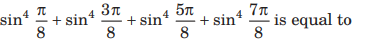
(a) 1
(b) 3/2
(c) 2
(d) 1/4 

Question: The value of cos π/65 cos 2π/65 cos 4π/65…cos 32π/65 is
(a) 1/32
(b) 1/64
(c) -1/32
(d) -1/64 

Question: The value of cos² A(3-4 cos² A)² + sin² A(3-4 sin² A)² is equal to
(a) cos 4 A
(b) sin 4 A
(c) 1
(d) None of these 

Question:

Question:

Question: If in a Δ ABC, ∠C = 90° , then the maximum value of sin A sin B is
(a) 1/2
(b) 1
(c) 2 
(d) None of these 

Question: If y = 1+ 4 sin2x, cos2 x,  then
(a) 1 ≤ y ≤ 2
(b) – 1 ≤ y ≤ 1
(c) – 3 ≤ y ≤ 3
(d) None of these 

Question: If 4nα =π, then the value of tanα· tan2α · tan3·  tan 4α … tan (2n-2)α tan (2n-1) α is
(a) 0
(b) 1
(c) -1
(d) None of these 

Question: The maximum value of cos²(π/3-x)-cos²(π /3+x)  is
(a) -√3/2
(b) 1/2
(c) 3/2
(d) 3/2 

Question: The maximum value of sin(x+π/6) +cos (x+π/6) the interval (0,π/2) is attained at
(a) x = π/12
(b) x = π/6
(c) x = π/3
(d) x = π/2 

Question. If in a Δ ABC, b+c/11 = c+a/12 = a+b/13 ,then cos A is equal to
(a) 1/5
(b) 5/7
(c) 19/35
(d) None of these

Question. In a DABC, 2ca sin A-B+C/2 is equal to
(a) a2 + b2 – c2
(b) c2 + a2 – b2
(c) b2 – c2 – a2
(d) c2 – a2 – b2

Question. If the angles of a triangle be in the ratio 1 : 2 : 7, then the ratio of its greatest side to the least side is
(a) 1 : 2
(b) 2 : 1
(c) (√5 + 1) : (√5 – 1)
(d) (√5 – 1) : (√5 + 1)

Question. The area of the circle and the area of a regular polygon ofnsides and of perimeter equal to that of the circle are in the ratio of
(a) tan :π/n , n/n
(b) cos :π/n , n/n
(c) sin :π/n , n/n
(d) cot :π/n , n/n

Question. The circumradius of an equilateral triangle of side 2√3 cm, is
(a) 1 cm
(b) √3 cm
(c) 2 cm
(d) 2√3 cm

Question. acosA cos bcosB c cosC/a+b+c is equal to
(a) 1/r
(b) rR /
(c) R/r
(d) 1/R

Question. If in a ΔABC, 8R² = a² + b² + c² , then the triangle is
(a) right angled
(b) isosceles
(c) equilateral
(d) None of these

Question. If r1, r2 , r3 have their usual meanings, then value of 1/r1 + 1/r2 + 1/r3 is
(a) 1
(b) 0
(c) 1/r
(d) None of the above

Question. The angle of elevation of the top of an incomplete vertical pillar at a horizontal distance of 100 m from its base is 45°. If the angle of elevation of the top of the complete pillar at the same point is 60°,then the difference in the height of complete and incomplete pillar is
(a) 50√2m
(b) 100 m
(c) 100(√3-1)m
(d) 100(√3+1)m

Question. A flag staff stands in the centre of a rectangular field whose diagonal is 1200 m and subtends angles 15° and 45° at the mid-points of the sides of the field. The height of the flag staff is
(a) 200 m
(b) 300 √2 + √3 m
(c) 300 √2 – √3 m
(d) 400 m

Question. A balloon is coming down at the rate of 4 m/min and its angle of elevation is 45° from a point on the ground which has been reduced to 30° after 10 min. Balloon will be on the ground at a distance of how many metres from the observer?
(a) 20√3
(b) 20(3 + √3)
(c) 10(3 + √3)
(d) None of these

Question. From an aeroplane vertically over a straight horizontal road, the angles of depression of two consecutive milestones on opposite sides of the aeroplane are observed to be a and b. The height in miles of the aeroplane above the road is
(a) tanα + tanβ/tanαtanβ
(b) tanαtanβ/tanα + tanβ
(c) cotαcotβ /cotα + cotβ
(d) None of these

Question. A tree is broken by wind, its upper part touches the ground at a point 10 m from the foot of the tree and makes an angle 45° with the ground. The entire length of tree is
(a) 15 m
(b) 20 m
(c) 10(1+ √2)m
(d) 10 (1+√3/2)

Question. Each side of a square subtends an angle of 60° at the top of a towerh metres high standing in the centre of the square. If ais the length of each side of the square, then
(a) 2a2 = h2
(b) 2h2 = h2
(c) 3a2 = 2h2
(d) 2h2 = 3a2

Question. From a station A due West of a tower the angle of elevation of the top of the tower is seen to be 45°. From a stationB, 10 metre from A and in the direction 45° South of East the angle of elevation is 30°, the height of the tower is
(a) 5√2(√5+1)m
(b) [5√2(√5+1)/2]m
(c) [5(√5+1)/2]m
(d)  None of these

Question. A vertical lamp-post 6 m high, stands at a distance of 2 m from a wall, 4 m high. A 1.5 m tall man starts to walk away from the wall on the other side of the wall, in line with the lamp-post. The maximum distance to which the man can walk remaining in the shadow is
(a) 5/2 m
(b) 3/2 m
(c) 4 m
(d) None of these

Question. If a, b and c are sides of a triangle, then
(a) √a + √b > √c
(b) √a – √b > √c (if c is smallest)
(c) √a + √b < √c
(d) None of the above

Question. In a ΔABC, ÐC = 60°, then 1/α+c + 1/b+c is equal to
(a) 1/a + b + c
(b) 2/a + b + c
(c) 3/a + b + c
(d) None of these

Question. In a ΔABC, if a , b and c are in AP, then the value of (sin A/2 sin C/2) sin B/2 is
(a) 1
(b) 1/2
(c) 2
(d) – 1

Question. In a triangle, the lengths of the two larger sides are 10 cm and 9 cm, respectively. If the angles of the triangle are in AP, then the length of the third side in cm can be
(a) 5 – √6 only
(b) 5 + √6 only
(c) 5 – √6 or 5 + √6
(d) neither 5 – √6 nor 5 + √6

Question. In a ΔABC, if 2 s = a + b + c, then the value of the s(s-a)/bs -(s-b)(s-c)/bc is equal to
(a) sin A
(b) cos A
(c) tan A
(d) None of these

Question. In a ΔABC, (b+c-a) tan A/2 is equal to
(a) 2Δ/s
(b) Δ/s
(c) Δs/bc
(d) (s/a)R

15. In a ΔPQR as shown in figure given that x : y : z : :2 :3 :6, then the value of ∠QPR is

(a) π/6
(b) π/4
(c) π/3
(d) None of the above

Question. In ΔABC, AD is median and ∠A = ^60°, then 4AD² is equal to
(a) b² + c² – bc
(b) 2b² + c² – 2bc
(c) b² + c² + 2bc
(d) None of these

Question. If cos2A+cos2C=sin2B = B, then DABC is
(a) equilateral
(b) right angled
(c) isosceles
(d) None of these

Question. The angle of elevation of the top of the tower observed from each of the three points A, B,C on the ground forming a triangle is the same ∠a. If R is the circumradius of the DABC, then the height of the tower is
(a) R sin α
(b) Rcos α
(c) Rcot α
(d) R tan α

Question. A spherical balloon of radius r subtends an Ða at the eye of an observer. If the angle of elevation of the centre of the balloon be b, then height of the centre of the balloon is
(a) (α/2)
(b) (β/2)
(c) r sin(α/2) cosecβ
(d) r sin α cosec (β/2)

Question. In a ∠ABC, a = 5, b = 7 and sin A = 3/4, then the number of possible triangles are
(a) 1
(b) 0
(c) 2
(d) infinite

Question. If p1 , p2 , and p3 are altitudes of a ΔABC drawn from the vertices A, B and C and Δ the area of the triangle, then p1-2 + p2-2 + p3–2
(a) a+b+c/Δ
(b) a2+b2+c2/4Δ2
(c) a2+b2+c2/Δ2
(d) None of these

Question. If in a ΔABC, sin A : sin B : sin C = 1: 2: 3, if b = 4 cm, then perimeter of the triangle is
(a) 6 cm
(b) 24 cm
(c) 12 cm
(d) 8 cm

Question. If in a ΔABC, atan + btanB = (a+b) tan(A+B/2) then
(a) A = B
(b) A = -B
(c) A = 2B
(d) B = 2A

Question. If two adjacent sides of a cyclic quadrilateral are 2 and 5 and the angle between them is 60°. If the third side is 3, then the remaining fourth side is
(a) 2
(b) 3
(c) 4
(d) 5

Question. If the sides of a triangle are in the ratio 3 : 7 : 8, then R : r is equal to
(a) 2 : 7
(b) 7 : 2
(c) 3 : 7
(d) 7 : 3

Question. In a triangle r1 r2 r3 > > , then
(a) a > b > c
(b) a < b < c
(c) a > b and b < c
(d) a < b and b > c

Question. A flag staff of 5 m high stands on a building of 25 m high. At an observer at a height of 30 m, the flag staff and the building subtend equal angles. The distance of the observer from the top of the flag staff is
(a) 5√3/2 m
(b) 5(√3/2) m
(c) 5(√2/3) m
(d) None of these

Question. The angles of depression of the top and the foot of a chimney as seen from the top of a second chimney, which is 150 m high and standing on the same level as the first areq and f respectively, then the distance between their tops when tan θ = 4/3 and tan Φ = 5/2, is
(a) 150/√3 m
(b) 100/√3 m
(c) 150 m
(d) 100 m

Question. From the tower 60mhigh angles of depression of the top and bottom of a house area andb, respectively. If the height of the house is 60sin(β – α) then x is equal to
(a) sin α sinβ
(b) cos α cosβ
(c) sin α cosβ
(d) cos α sinβ

Question. In a ∠ABC, a cot A + b cot B + c cotC is equal to
(a) r + R
(b) r – R
(c) 2 (r + R)
(d) 2 (r – R)

Question. In ΔABC, (a-b)2 cos2 (C/2) + sin2 C/2 is equal to
(a) a²
(b) b²
(c) c²
(d) None of these

Question. The inradius of the triangle whose sides are 3, 5, 6, is
(a) √(8/7)
(b) √8
(c) √7
(d) √(7/8)

Question. In an equilateral triangle, the ratio of the inradius, circumradius and exradius are
(a) 1 : 3 : 2
(b) 1 : 1 : 1
(c) 2 : 3 : 4
(d) 1 : 2 : 3

Question. If r₁ r₂ r₃ , and are exradii of any triangle, then r1 r2+r2r3+r3r1 is equal to
(a) Δ/r
(b) Δ2/r2
(c) r/Δ
(d) r2/Δ2

Question. In a ΔABC, if 2s = a + b + c and (s-b) (s-c) x sin2, A /2 , then the value of x is
(a) bc
(b) ca
(c) ab
(d) abc

Question. If the angles of a triangle are in the ratio 4 :1 :1, then the ratio of the longest side to the perimeter is
(a) 3 : (2 + 3)
(b) 1 : 6
(c) 1 : (2 + 3)
(d) 2 : 3

Question. In a ΔABC, cos A + cos B + cos C is equal to
(a) 1+r/R
(b) 1-r/R
(c) 1-R/r
(d) 1+R/r

Question. If a flag staff of 6 m high placed on the top of a tower throws a shadow of 2 3 m along the ground, then the angle (in degrees) that the sun makes with the ground is
(a) 60°
(b) 80°
(c) 75°
(d) None of these

Question. Inradius is equal to
(a) 2
(b) 1
(c) 1.5
(d) 2.5

Question. A ladder leaves again a wall at an ∠α to the horizontal. Its foot is pulled away through a distance a1, so that it slides a distance b1 down the wall and rests inclined at ∠β with the horizontal. It foot is further pulled aways through a2, so that it slides a further distance b2 down the wall and is now, inclined at an ∠γ. If a1a2   = b1 b2 , then
(a) α + β + γ is greater than π
(b) α + β + γ is equal to π
(c) α + β + γ is less than π
(d) nothing can be said about α + β + γ

We hope the above MCQ Questions Class 11 Mathematics Trigonometric Functions with answers based on the latest syllabus and examination guidelines issued by CBSE, NCERT and KVS are really useful for you. Trigonometric Functions is an important chapter in Class 11 as it provides very strong understanding about this topic. Students should go through the answers provided for the MCQs after they have themselves solved the questions. All MCQs have been provided with four options for the students to solve. These questions are really useful for benefit of class 11 students. Please go through these and let us know if you have any feedback in the comments section.