MCQs for Mathematics Class 11 with Answers Chapter 7 Permutations and Combinations
Students of class 11 Mathematics should refer to MCQ Questions Class 11 Mathematics Permutations and Combinations with answers provided here which is an important chapter in Class 11 Mathematics NCERT textbook. These MCQ for Class 11 Mathematics with Answers have been prepared based on the latest CBSE and NCERT syllabus and examination guidelines for Class 11 Mathematics. The following MCQs can help you to practice and get better marks in the upcoming class 11 Mathematics examination
Chapter 7 Permutations and Combinations MCQ with Answers Class 11 Mathematics
MCQ Questions Class 11 Mathematics Permutations and Combinations with answers provided below have been prepared by expert teachers of grade 11. These objective questions with solutions are expected to come in the upcoming Standard 11 examinations. Learn the below provided MCQ questions to get better marks in examinations.
Question. If 1/8! + 1/9! = x/10! , then find the value of x.
(a) 90
(b) 100
(c) 80
(d) 95
Answer
B
Question: If nC3+nC4 > n+1C3, , then
(a) n > 6
(b) n > 7
(c) n < 6
(d) None of these
Answer
A
Question:

Answer
C
Question: In how many ways can a student choose a program of 5 courses, if 9 courses are available and 2 specific courses are compulsory for every student?
(a) 34
(b) 36
(c) 35
(d) 37
Answer
C
Question:
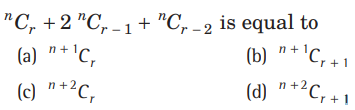
Answer
C
Question: Every body in a room shakes hands with everybody else. The total number of hand shakes is 66. The total number of persons in the room is
(a) 11
(b) 12
(c) 13
(d) 14
Answer
B
Question: A box contains two white balls, three black balls and four red balls. In how many ways can three balls be drawn from the box, if atleast one black ball is to be included in the draw?
(a) 64
(b) 45
(c) 46
(d) None of these
Answer
A
Question: The number of ways in which we can choose a committee from four men and six women so that the committee includes at least two men and exactly twice as many women as men is
(a) 94
(b) 126
(c) 128
(d) None of these
Answer
A
Question: The number of ways in which a team of eleven players can be selected from 22 players always including 2 of them and excluding 4 of them is
(a) 16C11
(b) 16C5
(c) 16C9
(d) 20C9
Answer
C
Question: There are 10 lamps in a hall. Each one of them can be switched on independently. Find the number of ways in which hall can be illuminated.
(a) 2 10-2
(b) 210-1
(c) 2 10 +1
(d) None of these
Answer
B
Question: A five digit number divisible by 3 is to be formed using the numbers 0,1,2,3, 4 and 5, without repetition. The total number of ways this can be done, is
(a) 216
(b) 240
(c) 600
(d) 3125
Answer
A
Question: A sports team of 11 students is to be constituted, choosing at least 5 from Class XI and at least 5 from Class XII. If there are 20 students in each of these classes, in how many ways can the team be constituted?
(a) 20C5x 20C6
(b) 2(20C5x20C6)
(c) 2(20C5)2
(d) None of these
Answer
B
Question: A pack of 52 cards are shuffled together. The number of ways in which a man can be dealt 26 cards so that he does not get two cards of the same suit and same denomination, is
(a) 52C26·226
(b) 104C26
(c) 2·52 C26
(d) None of these
Answer
A
Question: In how many ways can 21 English and 19 Hindi books be placed in a row so that no two Hindi books are together?
(a) 1540
(b) 1450
(c) 1504
(d) 1405
Answer
A
Question: Find the number of positive integers greater than 6000 and less than 7000 which are divisible by 5, provided that no digit is to be repeated.
(a) 111
(b) 112
(c) 113
(d) None of these
Answer
B
Question: 4 buses runs between Bhopal and Gwalior. If a man goes from Gwalior to Bhopal by a bus and comes back to Gwalior by another bus, then the total possible ways are
(a) 12
(b) 16
(c) 4
(d) 8
Answer
A
Question: In an examination, a student has to answer 4 questions out of 5 questions; questions 1 and 2 are however compulsory. Find the number of ways in which the student can make the choice.
(a) 3
(b) 2
(c) 4
(d) 5
Answer
A
Question: In a football championship, there were played 153 matches. Every team played one match with each other. The number of teams participating in the championship is
(a) 17
(b) 18
(c) 9
(d) 13
Answer
B
Question: A question paper is divided into two parts A and B and each part contains 5 questions. The number of ways in which a candidate can answer 6 questions selecting at least two questions from each part is
(a) 80
(b) 100
(c) 200
(d) None of these
Answer
C
Question: A father with 8 children takes them 3 at a time to the zoological gardens, as often as he can without taking the same 3 children together more than once. The number of times he will go the garden, is
(a) 336
(b) 112
(c) 56
(d) None of these
Answer
C
Question: A car will hold 2 in the front seat and 1 in the rear seat. If among 6 persons 2 can drive, then number of ways in which the car can be filled, is
(a) 10
(b) 20
(c) 30
(d) None of these
Answer
B
Question. Seven different letters are given. Then the number of ways in which words of 5 letters can be formed such that atleast one of the letters is repeated, is
(a) 7P5
(b) 14287
(c) 57
(d) 75
Answer
B
Question. If nC9 = nC8, then find nC17.
(a) 1
(b) 2
(c) 0
(d) 3
Answer
A
Question. The value of 10Cr/11Cr , when the numerator and denominator takes its greatest value, is
(a) 6/11
(b) 5/11
(c) 10/6
(d) 10/5
Answer
A
Question. Find the number of arrangements of the mletters of the word INDEPENDENCE when words begin with I and end in P.
(a) 12400
(b) 12420
(c) 12600
(d) 12620
Answer
C
Question. ABC is a triangle. 4, 5, 6 points are marked on the sides AB, BC, CA respectively, the number of triangles having vertices on different sides is
(a) (4 + 5 + 6)!
(b) (4 – 1) (5 – 1) (6 – 1)
(c) 5! 4! 6!
(d) 4 × 5 × 6
Answer
D
Question. Find the number of permutations of the letters of the word AHMEDABAD.
(a) 31250
(b) 28540
(c) 30240
(d) 31500
Answer
C
Question. Evaluate n!/r! (n – r) , then find the value of x.
(a) 10
(b) 12
(c) 14
(d) 16
Answer
A
Question. If 2n + 3C2n – 2n + 2C2n – 1 = 15(2n + 1), then n =
(a) 13
(b) 14
(c) 27
(d) 15
Answer
B
Question. How many different nine digit numbers can be formed from the number 223355888 by rearranging its digits so that the odd digits occupy even positions?
(a) 16
(b) 36
(c) 60
(d) 180
Answer
C
Question. The number of six digit numbers, whose all digits are odd (i.e., 1, 3, 5, 7, 9), is
(a) 65
(b) 56
(c) 6!/2!
(d) None of these
Answer
B
Question. Evaluate : (i) 5! (ii) 7!
(i) (ii) (i) (ii)
(a) 110, 5030
(b) 120, 5040
(c) 115, 5020
(d) 121, 5000
Answer
C
Question. Find the number of arrangements of the letters of the word INDEPENDENCE when vowels never occur together.
(a) 1646400
(b) 1646450
(c) 1640000
(d) 1646430
Answer
A
Question. Compute 9!/6! .
(a) 420
(b) 400
(c) 504
(d) 440
Answer
C
Question. There are four balls of different colours and four boxes of colours same as those of the balls.
The number of ways in which the balls, one in each box, could be placed such that a ball does not go to box of its own colour, is
(a) 8
(b) 7
(c) 9
(d) 10
Answer
C
Question. Four writers must write a book containing 17 chapters. The first and third writer must write 5 chapters each, the second writer must write 4 chapters and fourth writer must write three chapters. The number of ways that can be found to divide the book between four writers, is
(a) 17!/(5!)2 4!3!2!
(b) 17!/5!4!3!2!
(c) 17!/(5!)2 4!3!
(d) 17!/(5!)2 x 4 x 3
Answer
B
Question. Find the value of n such that nP nP n 5 = 42 3, > 4 .
(a) 10
(b) 15
(c) 12
(d) 20
Answer
A
Question. Find the number of permutations of the letters of the word ALLAHABAD.
(a) 7530
(b) 7540
(c) 7560
(d) 7500
Answer
C
Question. The triplet (x, y, z) is chosen from the set {1, 2, 3, … n}, such that x ≤ y < z. The number of such triplets is
(a) n3
(b) nC3
(c) nC2
(d) nC2 + nC3
Answer
D
Question. Evaluate 12C2.
(a) 66
(b) 65
(c) 60
(d) 64
Answer
A
Question. A library has a copies of one book, b copies of each of two books, c copies of each of three books and single copies of d books. The total number of ways in which these books can be arranged in a shelf, is
(a) (a+b+c+d!)/a!b!c!
(b) (a+2b+3c+d)!/a!(b!)2(c!)3
(c) (a+2b+3c+d)!/a!b!c!
(d) None of these
Answer
B
Question. Evaluate 8! – 4!.
(a) 49206
(b) 49400
(c) 49000
(d) 40296
Answer
D
Question. If m points on one straight line are joined to n points on another straight line. The number of points of intersection of the line segments thus formed is
(a) mC2nC 2 /4
(b) mn(m − 1)(n − 1)/4
(c) mC2 nC 2 /2
(d) mC2 + nC2
Answer
B
Question. In how many ways can 4 red, 3 yellow and 2 green discs be arranged in a row, if the discs of the same colour are indistinguishable?
(a) 1200
(b) 1220
(c) 1240
(d) 1260
Answer
D
Question. If 10Cx – 1 > 2 10Cx, then set of values of x is
(a) [1, 10]
(b) (7, ∞)
(c) {1, 2, 3}
(d) {8, 9, 10}
Answer
D
Question. Number of ways in which 3 boys and 3 girls (all are of different heights) can be arranged in a line so that boys as well as girls among themselves are in decreasing order of their heights (from left to right), is
(a) 6!
(b) 3! × 3! × 2!
(c) 10
(d) 20
Answer
D
Question. Find the number of ways of choosing 4 cards from a pack of 52 playing cards when four cards belong to four different suits.
(a) 413
(b) 133
(c) 135
(d) 134
Answer
D
Question. The number of circles that can be drawn out of 10 points of which 7 are collinear, is
(a) 120
(b) 113
(c) 85
(d) 86
Answer
C
Question. In how many ways a committee consisting of 3 men and 2 women can be chosen from 7 men and 5 women?
(a) 45
(b) 350
(c) 4200
(d) 230
Answer
B
Question. Find the number of ways of choosing 4 face cards from a pack of 52 playing cards.
(a) 495
(b) 493
(c) 490
(d) 492
Answer
A
Question. A crocodile is known to have not more than 68 teeth. The total number of crocodiles with different set of teeth, are
(a) 68
(b) 68!
(c) 1617
(d) 6868
Answer
C
Question. Find the number of ways of choosing two red cards and two black cards from a pack of 52 playing cards.
(a) 105620
(b) 105624
(c) 105625
(d) 105600
Answer
C
Question. How many 4-digit numbers can be formed by using the digits 1 to 9, if repetition of digits is not allowed?
(a) 3024
(b) 3026
(c) 3040
(d) 3014
Answer
A
Question. The number of ways you can find to pack 9 different books into five parcels if four of the parcels must contain two books each, is
(a) 945
(b) 9C2 × 7C2 × 5C2 × 3C2
(c) 9C2 × 7C2 × 5C2 × 3C2 ×5!
(d) None of these
Answer
A
Question. In a class, there are 27 boys and 14 girls. The teacher wants to select 1 boy and 1 girl to represent the class for a function. In how many ways can the teacher make this selection?
(a) 378
(b) 377
(c) 375
(d) 379
Answer
A
Question. If n–1C3 + n–1C4 > nC3, then
(a) n > 5
(b) n > 6
(c) n > 7
(d) None of these
Answer
C
Question. Find r, if 5 4Pr = 6 5Pr–1.
(a) 2
(b) 4
(c) 3
(d) 5
Answer
C
Question. The number of ways in which the digits of the number 125453752 can be rearranged such that no two 5’s come together, is
(a) 9!/3! 2!
(b) 7!/3! 2!
(c) 7C3. 6!/2!
(d) None of these
Answer
C
Question. Find the value of n such that nP4/n -1 P4 = 5/3 , n > 4 .
(a) 11
(b) 10
(c) 13
(d) 12
Answer
B
Question. The number of diagonals of a polygon of 30 sides is
(a) 225
(b) 350
(c) 405
(d) 210
Answer
C
Assertion & Reasoning Based
(a) Assertion and Reason both are correct statements and Reason is the correct explanation of Assertion.
(b) Assertion and Reason both are correct statements but Reason is not the correct explanation of Assertion.
(c) Assertion is correct statement but Reason is wrong statement.
(d) Assertion is wrong statement but Reason is correct statement.
Question. Assertion : Number of rectangles on a chess board is 8C2 × 8C2.
Reason : To form a rectangle, we have to select any two of the horizontal line and any two of the vertical line.
Answer
D
Question. Assertion : If n is a positive integer, then n(n2 – 1) (n +2) is divisible by 24.
Reason : Product of r consecutive whole numbers is divisible by r.
Answer
A
Question. Assertion : Number of lines formed by joining n points on a circle (n ≥ 2) is n (n – 1)/2.
Reason : C (n,2) = n(n – 1)/2 .
Answer
C
Question. Assertion : The number of ways of distributing 10 identical balls in 4 distinct boxes such that no box is empty is 9C3.
Reason : The number of ways of choosing any 3 places, from 9 different places is 9C3.
Answer
A
Question. Assertion : Product of five consecutive natural numbers is divisible by 4!
Reason : Product of n consecutive natural numbers is divisible by (n + 1)!.
Answer
C
We hope the above MCQ Questions Class 11 Mathematics Permutations and Combinations with answers based on the latest syllabus and examination guidelines issued by CBSE, NCERT and KVS are really useful for you. Permutations and Combinations is an important chapter in Class 11 as it provides very strong understanding about this topic. Students should go through the answers provided for the MCQs after they have themselves solved the questions. All MCQs have been provided with four options for the students to solve. These questions are really useful for benefit of class 11 students. Please go through these and let us know if you have any feedback in the comments section.
