MCQs for Mathematics Class 12 with Answers Chapter 1 Relations and Functions
Students of class 12 Mathematics should refer to MCQ Questions Class 12 Mathematics Relations and Functions with answers provided here which is an important chapter in Class 12 Mathematics NCERT textbook. These MCQ for Class 12 Mathematics with Answers have been prepared based on the latest CBSE and NCERT syllabus and examination guidelines for Class 12 Mathematics. The following MCQs can help you to practice and get better marks in the upcoming class 12 Mathematics examination
Chapter 1 Relations and Functions MCQ with Answers Class 12 Mathematics
MCQ Questions Class 12 Mathematics Relations and Functions provided below have been prepared by expert teachers of grade 12. These objective questions with solutions are expected to come in the upcoming Standard 12 examinations. Learn the below provided MCQ questions to get better marks in examinations.
Question: The domain of definition of the function y (x ) given by equation 2x +2y =2 is
(a) 0 < x ≤ 1
(b) 0 ≤x ≤1
(c) −∞ < x≤ 0
(d) −∞ < x <1
Answer
D
Question: If f (x)=[x2] -[x,]2, where [⋅] denotes the greatest integer function and x ∈[ 0,2] then the set of values of f (x) is
(a) {-1,0}
(b) { -1,0,1}
(c) {0}
(d) {0,1 2}
Answer
D
Question: Domain and Range of f (x) = x3+3×2+20x- sin x are respectively
(a) R, R
(b) R, R+
(c) R+, R +
(d) None of these
Answer
A
Question: Let f (x)= 1+b2)x2+2bx+1 and let m (b) be the minimum value of f (x) .As b varies, the range of m (b) is
(a) [0, 1]
(b) 0,1/2]
(c) [1/2,1]
(d) (0, 1]
Answer
D
Question: The function f: R → R : → defined by f(x)= |( x-1)(x-2)| is
(a) one one onto
(b) one one into
(c) many one onto
(d) many one into
Answer
D
Question:
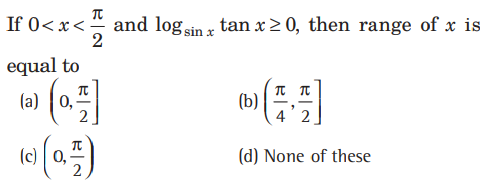
Answer
D
Question: Let R be the set of real numbers and f: R → R be the function defined by f (x) = 4x +5, then f is
(a) injective
(b) surjective
(c) invertible
(d) None of these
Answer
C
Question: Let f :R → R be defined by f (x)= x2+1. Then, pre-images of 17 and –3, respectively are
(a) φ − , {4 ,4 }
(b) {3 ,3 } φ
(c) {4 ,4 }, φ
(d) {4 ,-4 }, {2,-2}
Answer
C
Question: The function f: R → R defined by f (x) =x/x2+1′ ∀ x ∈ R is
(a) one one and onto
(b) neither one one nor onto
(c) one one
(d) on to
Answer
B
Question: Set A has 3 elements and the set B has 4 elements.
Then, the number of injective mappings that can be defined from A to B is
(a) 144
(b) 12
(c) 24
(d) 64
Answer
C
Question: The modulus function f: R→ R, given by f (x)= |x|, where| x| is x, if x is non-negative and|x| is −x, if x is negative is
(a) neither one one nor onto
(b) one one onto
(c) one one but not onto
(d) None of the above
Answer
A
Question: If f:[0, π/2]→[0,∞) be a function defined by y=sin (x/2), then f is
(a) injective
(b) surjective
(c) bijective
(d) None of these
Answer
A
Question: Let A= R− {3 } and B= R- {1 } . Consider the function f: A → B defined by f (x)=(x-2/x-3) is
(a) f is only one one
(b) f is one one but not onto
(c) f is one one and onto
(d) None of these
Answer
C
Question: Let A = {1,2,3}, B = {4 ,5 , 6,7 } and let f = {(1 , 4), (2,5 ), (3, 6)} be a function from A to B, then f is
(a) one one
(b) many one
(c) one one onto
(d) None of these
Answer
A
Question: The greatest integer function f :R → R, given by f (x)= [x], = where [x] denotes the greatest integer less than or equal to x, is
(a) one one onto
(b) one one
(c) on to
(d) neither one one nor onto
Answer
D
Question:

(a) onto
(b) one one
(c) bijective
(d) None of these
Answer
A
Question: Let E = {1, 2, 3, 4} and F = { 1, 2}. Then, the number of onto functions from E to F is
(a) 14
(b) 16
(c) 12
(d) 8
Answer
A
Question: Let the function f : R : → R be defined by f (x )= cos x, ∀ x ∈ R, then f is
(a) one one and onto
(b) only one one
(c) only onto
(d) neither one one nor onto
Answer
D
Question: Which of the following is a bijective function on their ranges?
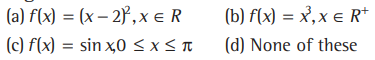
Answer
B
Question: Let f:(e, ∞) → be defined by f (x) = log[log(log x)], then f is
(a) one one onto
(b) many one onto
(c) one one into
(d) many one into
Answer
A
Question. Let A and B be finite sets containing m and n elements respectively. The number of relations that can be defined from A to B is
(a) 2mn
(b) 2m+n
(c) mn
(d) 0
Answer
A
Question. Let A = {1, 2, 3} and consider the relation R = {(1, 1), (2, 2), (3, 3), (1, 2), (2, 3), (1, 3)}. Then R is
(a) reflexive but not symmetric
(b) reflexive but not transitive
(c) symmetric and transitive
(d) neither symmetric nor transitive
Answer
A
Question. For real numbers x and y, define xRy if and only if x – y + 2 is an irrational number. Then the relation R is
(a) reflexive
(b) symmetric
(c) transitive
(d) none of these
Answer
A
Question. Let f : R → R be the functions defined by f(x) = x3 + 5. Then f–1(x) is
(a) (x 5) 1/3
(b) (x – 5) 1/3
(c) (5 – x) 1/3
(d) 5 – x
Answer
B
Question. The maximum number of equivalence relation on the set A = {1, 2, 3} are
(a) 1
(b) 2
(c) 3
(d) 5
Answer
D
Question. Let f : R → R be defined by f(x) = sin x and g : R → R be defined by g(x) = x2, then fog is
(a) x2 sin x
(b) (sin x)2
(c) sin x2
(d) sinx/x2
Answer
C
Question. Let A = {1, 2, 3}. Then number of relations containing (1, 2) and (1, 3) which are reflexive and symmetric but not transitive is
(a) 1
(b) 2
(c) 3
(d) 4
Answer
D
Question. Let f : R –{3/5 R be defined by f (x) = 3x+2 /5x–3. Then
(a) f –1(x) = f(x)
(b) f –1(x) = – f(x)
(c) fo f(x) = – x
(d) f-1 (x) 1/19 f (x)
Answer
A
Question. Let A = {1, 2, 3}. Then number of equivalence relations containing (1, 2) is/are
(a) 1
(b) 2
(c) 3
(d) 4
Answer
B
Question. If f(x) = sin2 x and the composite function g(f(x)) = |sin x|, then g(x) is equal to
(a) √x + 1
(b) √x – 1
(c) √x
(d) –√x
Answer
C
Question. Set A has 3 elements and the set B has 4 elements. Then the number of injective mapping that can be defined from A to B is
(a) 144
(b) 12
(c) 24
(d) 64
Answer
C
Question. If A = {a, b, c, d}, then a relation R = {(a, b), (b, a), (a, a)} on A is
(a) symmetric only
(b) transitive only
(c) reflexive and transitive
(d) symmetric and transitive only
Answer
D
Question. The function f : R → R defined by f(x) = 2x + 2|x| is
(a) One-one and onto
(b) Many-one and onto
(c) One-one and into
(d) Many-one and into
Answer
C
Question. If the set A contains 5 elements and the set B contains 6 elements, then the number of one-one and onto mapping from A to B is
(a) 720
(b) 120
(c) 0
(d) none of these
Answer
C
Question. Consider the non-empty set consisting of children in a family and a relation R defined as aRb if a is brother of b. Then R is
(a) symmetric but not transitive
(b) transitive but not symmetric
(c) neither symmetric nor transitive
(d) both symmetric and transitive
Answer
B
Question. Which of the following functions from z into z is bijection?
(a) f(x) = x3
(b) f(x) = x + 2
(c) f(x) = 2x + 1
(d) f(x) = x2 + 1
Answer
B
Question. The relation R in the set A = {1, 2, 3, 4} given by R = {(1, 2), (2, 2), (1, 1), (4, 4), (1, 3), (3, 3), (3, 2)} is
(a) reflexive and symmetric but not transitive
(b) reflexive and transitive but not symmetric
(c) symmetric and transitive but not reflexive
(d) an equivalence relation
Answer
B
Question. Let R be a relation on the set N of natural numbers defined by nRm if n divides m. Then R is
(a) reflexive and symmetric
(b) transitive and symmetric
(c) equivalence
(d) reflexive, transitive but not symmetric
Answer
D
Question. Let f : [2, ∞) → R be the function defined by f(x) = x2 – 4x + 5, then the range of f is
(a) R
(b) [1, ∞)
(c) [4, ∞)
(d) [5, ∞)
Answer
B
Question. Let f : R → R be defined by f(x) = x2 + 1. Then, pre-images of 17 and –3, respectively, are
(a) f, {4, –4}
(b) {3, –3}, f
(c) {4, –4}, f
(d) {4, –4}, {2, –2}
Answer
C
Question. Let L denotes the set of all straight lines in a plane. Let a relation R be defined by lRm if and only if l is perpendicular to m ∀ l, m ∈ L. Then R is
(a) reflexive
(b) symmetric
(c) transitive
(d) none of these
Answer
B
Question. Let f : R → R be defined by f(x) = 3x2 – 5 and g : R → R by g(x) = x /x2 + 1 . Then gof is
(a) 3x2 –5 /9x4 –30x2 + 26
(b) 3x2 –5 /9x4 –6x2 + 26
(c) 3x2 /x4 –2x2 – 4
(d) 3x2 /9x4 –30x2 – 2
Answer
A
Question. If a relation R on the set {1, 2, 3} be defined by R = {(1, 2)}, then R is
(a) reflexive
(b) transitive
(c) symmetric
(d) none of these
Answer
B
Question. If A = {1, 2, 3}, B = {1, 4, 6, 9} and R is a relation from A to B defined by ‘x is greater than y’.
Then range of R is
(a) {1, 4, 6, 9}
(b) {4, 6, 9}
(c) {1}
(d) none of these
Answer
C
Question. Let f : R → R be defined by f(x) = 3x – 4. Then f –1(x) is given by
(a) (x +4)/3
(b) x/3– 4
(c) 3x + 4
(d) none of these
Answer
A
Question. The inverse of the function

Answer
B
Question. If f : R → S, defined by f (x) = sin x – √3 cos x +1, is onto, then the interval of S is
(a) [ –1, 3]
(b) [–1, 1]
(c) [ 0, 1]
(d) [0, 3]
Answer
A
Question. Let R be the relation defined in the set A of all triangles as R = {(T1, T2) : T1 is similar to T2}. If R is an equivalence relation and there are three right angled triangles T1 with sides 3, 4, 5; T2 with sides 5, 12, 13 and T3 with sides 6, 8, 10. Then,
(a) T1 is related to T2
(b) T2 is related to T3
(c) T1 is related to T3
(d) None of these
Answer
C
Question. For the set A = {1, 2, 3}, define a relation R in the set A as follows
R = {(1, 1), (2, 2), (3, 3), (1, 3)}
Then, the ordered pair to be added to R to make it the smallest equivalence relation is
(a) (1, 3)
(b) (3, 1)
(c) (2, 1) (d) (1, 2)
Answer
B
Question. If a * b denote the bigger among a and b and if a x b = (a x b) + 3, then 4×7 =
(a) 14
(b) 31
(c) 10
(d) 8
Answer
C
Question. Consider the following statements
I. Addition, subtraction and multiplication are binary operations on R.
II. Division is a binary operation on R but not a binary operation on non-zero real numbers.
(a) Only I is true
(b) Only II is true
(c) Both I and II are true
(d) Neither I nor II is true
Answer
A
Question. Let A = {1, 2, 3}. Then, the number of relations containing (1, 2) and (1, 3), which are reflexive and symmetric but not transitive, is
(a) 1
(b) 2
(c) 3
(d) 4
Answer
A
Question. The number of all one-one functions from set A = {1, 2, 3} to itself is
(a) 2
(b) 6
(c) 3
(d) 1
Answer
B
Question. If the function gof is defined and is one-one then
(a) neither f nor g is one-one
(b) f and g both are necessarily one-one
(c) g must be one-one
(d) None of the above
Answer
D
Question. Which one of the following relations on the set of real numbers R is an equivalence relation ?
(a) aR1b ⇔| a | = | b |
(b) aR2b ⇔ a ≥ b
(c) aR3b⇔a divides b
(d) aR4b⇔a < b
Answer
A
Question. If f : B → A is defined by f(x) = 3x+4/5x-7 and g : A → B is defined by g(x) = 7x+4/5x-3 , where A = R – {3/5} and B = R – {7/5} and IA is an identity function on A and IB is identity function on B, then
(a) fog = IA and gof = IA
(b) fog = IA and gof = IB
(c) fog = IB and gof = IB
(d) fog = IB and gof = IA
Answer
B
Question. If f : R → R be given by f(x) = (3-x3)1/3 , then fof (x) is
(a) x1/3
(b) x3
(c) x
(d) (3 – x3)
Answer
C
Question. The relation R on the set Z defined by R = {(a, b) : (a – b) is divisible by 5} divides the set Z into how many disjoint equivalence classes ?
(a) 5
(b) 2
(c) 3
(d) 4
Answer
A
Question. For a binary operation * on the set {1, 2, 3, 4, 5}, consider the following multiplication table.

Which of the following is correct?
(a) (2 * 3) * 4 = 1
(b) 2 * (3 * 4) = 2
(c) * is not commutative
(d) (2 * 3) * (4 * 5) = 2
Answer
A
Question. The number of equivalence relations in the set {1, 2, 3} containing (1, 2) and (2, 1) is
(a) 2
(b) 3
(c) 1
(d) 4
Answer
A
Question. Consider the following statements
I. The operation * defined on Z+ by a * b = |a – b| is a binary operation.
II. The operation * defined on Z+ by a * b = a is not a binary operation.
(a) Only I is true
(b) Only II is true
(c) Both I and II are true
(d) Neither I nor II is true
Answer
A
Question. On the set N of all natural numbers, define the relation R by a R b, iff GCD of a and b is 2. Then, R is
(a) reflexive, but not symmetric
(b) symmetric only
(c) reflexive and transitive
(d) not reflexive, not symmetric, not transitive
Answer
B
Question. A function f : R → [–1, 1] defined by f(x) = sin x, ∀ x ∈ R, where R is the subset of real numbers is one-one and onto if R is the interval :
(a) [0,2π]
(b) [-π/2 , π/2]
(c) [-π , π]
(d) (0,π]
Answer
B
Question. The number of surjective functions from A to B where A = {1, 2, 3, 4} and B = {a, b} is
(a) 14
(b) 12
(c) 2
(d) 15
Answer
A
Assertion Reason Type Questions :
(a) Assertion is correct, reason is correct; reason is a correct explanation for assertion.
(b) Assertion is correct, reason is correct; reason is not a correct explanation for assertion
(c) Assertion is correct, reason is incorrect
(d) Assertion is incorrect, reason is correct.
Question. Assertion : If f : R → R and g : R → R be two mappings such that f(x) = sin x and g(x) = x2, then fog ≠ gof.
Reason : (fog) x = f(x) g(x) = (gof) x
Answer
C
Question. Assertion : Division is a binary operation on the set of natural numbers.
Reason : 5 ÷ 4 = 1.25 is not a natural number.
Answer
D
Question. Assertion : Let f : R → R be defined by f(x) = 1/x , then f is one-one and onto.
Reason : x = 0 does not belong to the domain of f.
Answer
D
Question. Let f(x) = (x +1)2 –1, x ≥ –1
Assertion : The set {x : f (x) = f –1(x) = {0, –1}
Reason : f is a bijection.
Answer
C
Question. Assertion : Let L be the set of all lines in a plane and R be the relations in L defined as R = {(L1, L2) : L1 is perpendicular to L2}. This relation is not equivalence relation.
Reason : A relation is said to be equivalence relation if it is reflexive, symmetric and transitive.
Answer
A
Question. Assertion : The function f : R → R given by f(x) = x3 is injective.
Reason : The function f : X → Y is injective, if f(x) = f(y) ⇒ x = y for all x, y ∈ X.
Answer
A
Question. Assertion : f : R → R defined by f (x) = sin x is a bijection.
Reason : If f is both one-one and onto it is bijection.
Answer
D
Question. Assertion : If f(x) is odd function and g(x) is even function, then f(x) + g(x) is neither even nor odd.
Reason :
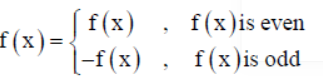
Answer
A
Question. Assertion : The binary operation subtraction on the set of real numbers is not commutative.
Reason : If a and b are two real numbers, then in general a – b ≠ b – a
Answer
A
One Word Answer
Question. A relation from a set A to a set B is a ___________ of A × B.
Answer
Subset
Question. A relation R from set A to set B is said to be ___________ if R = A × B.
Answer
The universal relation
Question. If any set A contains n elements. Then, the total number of injective functions from A onto itself is _________ .
Answer
n!
Question. The domain of the function f : R → R defined by f (x) = x2 – 3x + 2 is ___________ .
Answer
(– ∞, 1] ∪ [2, ∞)
Question. If f(x) = {4 – (x – 7)3}, then f –1(x) = ___________ .
Answer
7 (4 – x) 1/3

We hope the above multiple choice questions for Class 12 Mathematics for Chapter 1 Relations and Functions provided above with answers based on the latest syllabus and examination guidelines issued by CBSE, NCERT and KVS are really useful for you. Relations and Functions is an important chapter in Class 12 as it provides very strong understanding about this topic. Students should go through the answers provided for the MCQs after they have themselves solved the questions. All MCQs have been provided with four options for the students to solve. These questions are really useful for benefit of class 12 students. Please go through these and let us know if you have any feedback in the comments section.
