MCQs for Mathematics Class 12 with Answers Chapter 10 Vector Algebra
Students of class 12 Mathematics should refer to MCQ Questions Class 12 Mathematics Vector Algebra with answers provided here which is an important chapter in Class 12 Mathematics NCERT textbook. These MCQ for Class 12 Mathematics with Answers have been prepared based on the latest CBSE and NCERT syllabus and examination guidelines for Class 12 Mathematics. The following MCQs can help you to practice and get better marks in the upcoming class 12 Mathematics examination
Chapter 10 Vector Algebra MCQ with Answers Class 12 Mathematics
MCQ Questions Class 12 Mathematics Vector Algebra provided below have been prepared by expert teachers of grade 12. These objective questions with solutions are expected to come in the upcoming Standard 12 examinations. Learn the below provided MCQ questions to get better marks in examinations.
Question. The vectors 3î – ĵ + 2k̂, 2î + ĵ + 3k̂ and iî + mĵ – k̂ are coplanar if
(a) –2
(b) 0
(c) 2
(d) Any real number
Answer
A
Question.

Answer
(A,B,C)
Question. If a and b are two vectors and angle between them is θ, then
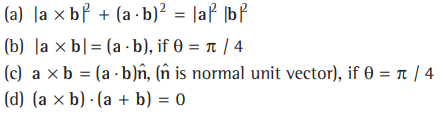
Answer
(A,B,C,D)
Question. Unit vectors a and b are perpendicular and unit vector c is inclined at an angle θ to both a and b. If c= αa +βb+Y(a x b),) then
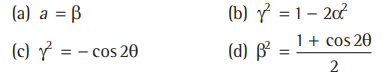
Answer
(A,B,C,D)
Question. If vectors a and b are non-collinear, then

(a) a unit vector
(b) in the plane of a and b
(c) equally inclined to a and b
(d) perpendicular to
Answer
(B,C ,D)
Question. Let a and b be two non-zero perpendicular vectors. A vector r satisfying the equation r x b = a can be
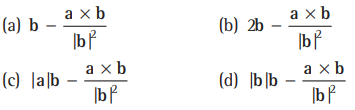
Answer
(A,B,C,D)
Vectors x, y and z each of magnitude √2 make angle of 60° with each other. x x(y x z)=a, y x (z x x)=b
Question.

Answer
C
Question.

Answer
D
Question. Vector z is

Answer
B
Question. Let a and b be two unit vectors. If the vectors c =a+2b and D = 5a-4b are perpendicular to each other, then the angle between

(a) π/6
(b) π/2
(c) π/3
(d) π/4
Answer
C
Question.

(a) -3
(b) 5
(c) 3
(d) -5
Answer
D
Question.

(a) √18
(b) √72
(c) √33
(d) √45
Answer
C
Question. Let ABCD be a parallelogram such that AB =q, AB =p, and ∠BAD be an acute angle. If r is the vector that coincides with the altitude directed from the vertex B to the side AD, then r is given by
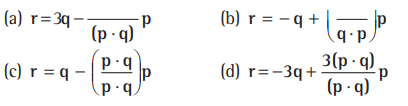
Answer
B
Question. The vectors a and b are not perpendicular c and d are two vectors satisfying b x c = b x d and a· d = 0.
Then, the vectors d is equal to

Answer
C
Question. Let a, b and c be three non-zero vectors which are pairwise non-collinear. If a+3b is collinear with c and b+ 2c is collinear with a, then a+ 3b+ 6c is
(a) a+ c
(b) a
(c) c
(d) 0
Answer
D
Question.

(a) (-3, 2)
(b) (2,-3
(c) (-2,3)
(d) (3,-2)
Answer
A
Question. A square piece of tin of side 18 cm is to be made into a box without top, by cutting off square from each corner and folding up the flaps of the box. What should be the side of the square to be cut-off so that the volume of the box is maximum possible?
(a) 3 cm
(b) 4 cm
(c) 5 cm
(d) 9 cm
Answer
A
Question. The two positive numbers whose sum is 16 and the sum of whose cubes is minimum, are
(a) 4 and 12
(b) 6 and 10
(c) 8 and 8
(d) None of these
Answer
C
Question. The right circular cone of least curved surface area and given volume has an altitude equal to
(a) two times the radius of the base.
(b) √3 times the radius of the base.
(c) √2 times the radius of the base.
(d) None of the above
Answer
C
Question. The closed right circular cylinder of given surface and maximum volume is such that its height is equal to
(a) the radius of the base
(b) the diameter of the base
(c) the twice of diameter of the base
(d) None of the above
Answer
B
Question. The semi-vertical angle of the cone of the maximum volume and of given slant height is
(a) tan-1√3
(b) tan-1√2
(c) tan-1(1/√2)
(d) None of the above
Answer
B
Question. The point on the curve x2=2y which is nearest to the point (0,5) is
(a) ( 2√2,4)
(b) (2√2,0)
(c) (0, 0)
(d) (2,2)
Answer
A
Question. The semi-vertical angle of right circular cone of given surface area and maximum volume is
sin– 1(1/3)·
(a) sin-1(1/3)
(b) sin-1(1/2)
(c) sin-1(√3)
(d) None of these
Answer
A
Question. The maximum area of an isosceles triangle inscribed in the ellipse x2/a2 + y2/b2= 1 with its vertex at one end of the major axis.
(a) 3/4ab sq unit
(b) 3/4 √3 ab sq unit
(c) √3/4 ab sq unit
(d) None of these
Answer
B
Question. A window is in the form of a rectangle surmounted by a semi-circle opening. The perimeter of the window is 10 m. The dimensions of the window to admit maximum light through the whole opening is
(a) length = breadth =1/π+4
(b) length = 20/π+4 and breadth =10/π+4
(c) length = 2/π+4 and breadth =1/π+4
(d) None of the above
Answer
B
Question. The sum of the perimeter of a circle and square is k, where k is some constant, then the sum of their areas is least when the side of square is
(a) equal to the radius of the circle
(b) double the radius of the circle
(c) triple the radius of the circle
(d) None of the above
Answer
B
Question. The altitude of the right circular cone of maximum volume that can be inscribed in a sphere of radius r is
(a) r/2
(b) r/3
(c) 3r/4
(d) 4r/3
Answer
D
Question. The height of the cylinder of maximum volume that can be inscribed in a sphere of radius R and the maximum volume respectively

Answer
A
Question. If the sum of the length of the hypotenuse and a side of a right angled triangle is given. Then, the area of the triangle is maximum when the angle between them is
(a) π/6
(b) π/4
(c) π/3
(d) π/2
Answer
C
Question. The height of the cylinder of greatest volume which can be inscribed in a circular cone of height h and having semi-vertical angle a and the greatest volume of cylinder are respectively

Answer
C
Question. Maximum slope of the curve y =-x3+3×2+9x-27 is
(a) 0
(b) 12
(c) 16
(d) 32
Answer
B
Question. If P, Q and P, R are the two sides of a triangle, then the angle between them which gives maximum area of the triangle, is
(a) π
(b) π / 3
(c) π / 4
(d) π / 2
Answer
D
Question. If ab = 2a+3b,a>0,b>0,then the minimum value of ab is
(a) 12
(b) 24
(c) 1/4
(d) None of these
Answer
B
Question. The minimum radius vector of the curve a2/x2+ b2/y2=1 is of length
(a) a- b
(b) a+ b
(c) 2a +b
(d) None of these
Answer
B
Question. if a2x4+b2y4=c6, then maximum value of xy is
(a) c2/√ab
(b)c3/ab
(c) c3/√2ab
(d) c3/2ab
Answer
B
Question. The perimeter of a sector is p. The area of the sector is maximum, when its radius is
(a) √p
(b) 1/√p
(c) p/2
(d) p/4
Answer
D
Question. If xy= c2 , then minimum value of xy is
(a) c√ab
(b)2c√ab
(c) -c√ab
(d) -2c√ab
Answer
B
Question. If a🠖 = 4 and –3 ≤ λ ≥ 2, then the range of |λa🠖| is
(a) [0, 8]
(b) [– 12, 8]
(c) [0, 12]
(d) [8, 12]
Answer
C
Question. The area of a triangle formed by vertices O, A, B where OA = î + 2ĵ + 3k̂→OA and →OB= –3î – 2ĵ + k̂
(a) 3√5 sq. units
(b) 5√5 sq. units
(c) 6 5 sq. units
(d) 4 sq. units
Answer
A
Question. The position vector of the point which divides the join of point 2a🠖– 3b🠖and a🠖 + b🠖 in the ratio 3 : 1 is
(a) 3a🠖– 3b🠖/2
(b) 7a🠖– 8b🠖/4
(c) 3a🠖/4
(d) 5a🠖/4
Answer
D
Question. The position vector of the point which divides the join of points with position vectors a🠖+ b🠖and 2a🠖 – b🠖 in the ratio 1 : 2 is
(a) 3a🠖+ 2b🠖 /3
(b) a🠖
(c) 5a🠖+ b🠖 /3
(d) 4a🠖+ b🠖 /3
Answer
D
Question. The vector having initial and terminal points as (2, 5, 0) and (–3, 7, 4) respectively is
(a) î – 12ĵ + 4k̂
(b) 5î – 2ĵ + 4k̂
(c)-5î + 2ĵ + 4k̂
(d) î – ĵ + k̂
Answer
C
Question. The angle between two vectors a🠖 and b🠖 with magnitudes 3 and 4 respectively and a🠖. b🠖 = 2√3 is
(a) π/6
(b) π/3
(c) π/2
(d) 5π/2
Answer
B
Question. If a🠖, b🠖 and c🠖 are three vectors such that a🠖 + b🠖 + c🠖 = 0 and a🠖 = 2, b🠖 = 3, c🠖= 5, then value
of a🠖. b🠖 +b🠖.c🠖+ c🠖. a🠖 is
(a) 0
(b) 1
(c) – 19
(d) 38
Answer
C
Question. Find the value of λ such that the vectors a🠖 = 2î + mĵ + k̂ and b🠖 = î + 2ĵ + 3k̂ are orthogonal
(a) 0
(b) 1
(c) 3/2
(d) -5/2
Answer
D
Question. The value of λ for which the vectors 3î – 6ĵ + k̂ and 2î – 4ĵ + mk̂ are parallel is
(a) 2/3
(b) 3/2
(c) 5/2
(d) 2/5
Answer
A
Question. The vector from origin to the points A and B are a = 2î – 3ĵ + 2k̂ and b = 2î + 3ĵ + k̂, respectively then the area of triangle OAB is
(a) 340
(b) 25
(c) 229
(d) (1/2)√229
Answer
D
Question. For any vector a🠖, the value of (a🠖 × î)2+(a🠖 × ĵ)2+(a🠖 × k̂)2 is equal to
(a) a🠖2
(b) 3a🠖2
(c) 4a🠖2
(d) 2a🠖2
Answer
D
Question. If |a🠖| = 10, |b🠖| = 2 and a🠖 . b🠖 = 12, then value of a🠖 × b🠖 is
(a) 5
(b) 10
(c) 14
(d) 16
Answer
D
Question. The vector λî + ĵ + 2k̂, î + λĵ – k̂ and 2î – ĵ + λk̂ are coplanar if
(a) λ = –2
(b) λ = 0
(c) λ = 1
(d) λ = – 1
Answer
A
Question. The value of î. (ĵ×k̂) + ĵ. (î×k̂) + k̂. (î×ĵ) is
(a) 0
(b) – 1
(c) 1
(d) 3
Answer
B
Question. If a🠖, b🠖, c🠖 are unit vectors such that a🠖+ b🠖+ c🠖 = 0, then the value of a🠖 .b🠖+ b🠖. c🠖 + c🠖. a🠖 is
(a) 1
(b) 3
(c) –3/2
(d) None of these
Answer
C
Question. The number of vectors of unit length perpendicular to the vectors a🠖 = 2î + ĵ + 2k̂ and b🠖 = ĵ + k̂ is
(a) one
(b) two
(c) three
(d) infinite
Answer
B
Question. The vector of the direction of the vector î – 2ĵ + 2k̂ that has magnitude 9 is
(a) î – 2ĵ + 2k̂
(b) î – 2ĵ + 2k̂/3
(c) 3(î – 2ĵ + 2k̂)
(d) 9(î – 2ĵ + 2k̂)
Answer
Question. Let a🠖 and b🠖 be two unit vectors and θ is the angle between them. Then a🠖 + b🠖is unit vector if q is
(a) π/4
(b) π/3
(c) π/2
(d) 2π/3
Answer
Question. The magnitude of the vector 6î + 2ĵ + 3k̂ is
(a) 5
(b) 7
(c) 12
(d) 1
Answer
Question. Let a🠖 = î – 2ĵ + 3k̂. If b is a vector such that a🠖. b🠖 |b🠖|2 and |a🠖 – b🠖 = √7 then |b🠖| equals
(a) 7
(b) 14
(c) 7
(d) 21
Answer
C
Question. The value of p for which p(î + ĵ + k̂) is a unit vector is
(a) 0
(b) 1/√3
(c) 1
(d) 3
Answer
B
Question . The area of the parallelogram whose diagonals are 2î and –3k̂ is ___________ square units. 3 sq. units
Answer
Question. The sine of the angle between vectors a🠖 = 2î – 6ĵ – 3k̂ and b🠖 = 4î + 3ĵ – k̂ is equal to _________. 5/√26
Answer
Question. The value of l for which the vectors 2î – mĵ + k̂ and it + 2ĵ – k̂ are orthogonal is ____________. λ=1/2
Answer
Question. If a🠖 = 3î – 2ĵ + 2k̂, b🠖 = 6î + 4ĵ – 2k̂ and c = –3it – 2ĵ + 4k̂. Then a🠖 . _b🠖 # c i is equal to _________. 72
Answer
Question. The vectors a🠖 = 3î – 2ĵ + 2k̂ and b🠖 = –î –2k̂ are the adjacent sides of a parallelogram. The acute angle between its diagonals is _____________ π/4
Answer
Question. The projection of the vector î – ĵ on the vector î + ĵ is _____________ . 0
Answer
Question. If |a🠖 b🠖|2 + |a🠖.b🠖|2 144 and |a🠖| 4 , then |b🠖| is equal to _____________ . 3
Answer
Question. If a is a non-zero vector, then _(a .î)î +`(a . ĵ)ĵ +_(a . k̂)k̂ equals _____________ . a🠖
Answer
4 Question. If |a🠖| = 1 and a🠖 x î = ĵ , then angle between a🠖 and î is _____________ . π/2
Answer
Question. The area of the triangle whose adjacent sides are a🠖 = î + 4ĵ – k̂ and b = î + ĵ + 2k̂ is _____________ sq. units. 3/2√11 Sq. units.
Answer

We hope the above multiple choice questions for Class 12 Mathematics for Chapter 10 Vector Algebra provided above with answers based on the latest syllabus and examination guidelines issued by CBSE, NCERT and KVS are really useful for you. Vector Algebra is an important chapter in Class 12 as it provides very strong understanding about this topic. Students should go through the answers provided for the MCQs after they have themselves solved the questions. All MCQs have been provided with four options for the students to solve. These questions are really useful for benefit of class 12 students. Please go through these and let us know if you have any feedback in the comments section.
