MCQs for Mathematics Class 12 with Answers Chapter 3 Matrices
Students of class 12 Mathematics should refer to MCQ Questions Class 12 Mathematics Matrices with answers provided here which is an important chapter in Class 12 Mathematics NCERT textbook. These MCQ for Class 12 Mathematics with Answers have been prepared based on the latest CBSE and NCERT syllabus and examination guidelines for Class 12 Mathematics. The following MCQs can help you to practice and get better marks in the upcoming class 12 Mathematics examination
Chapter 3 Matrices MCQ with Answers Class 12 Mathematics
MCQ Questions Class 12 Mathematics Matrices provided below have been prepared by expert teachers of grade 12. These objective questions with solutions are expected to come in the upcoming Standard 12 examinations. Learn the below provided MCQ questions to get better marks in examinations.
Question. If A =
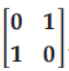
then A2 is equal to

Answer
D
Question: Let P and Q be 3x 3matrices p ≠ Q. If P3=Q3 = and
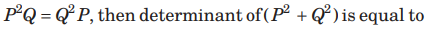
(a) – 2
(b) 1
(c) 0
(d) – 1
Answer
B
Question: Let A =

(a) there exists exactly one B such that AB BA =
(b) there exists infinitely many B’s such that AB BA =
(c) there cannot exist any B such that AB BA =
(d) there exist more than but finite number of B ’s such that
AB= BA
Answer
D
Question: The number of values of k for which the linear equations 4x+ky +2z=0, kx++4y+z=0 and 2x +2y+z=0 posses a non-zero solution is
(a) 2
(b) 1
(c) zero
(d) 3
Answer
B
Question: If P =
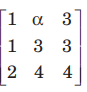
is the adjoint of 3x 3 matrix A and| A|= 4, then α is equal to
(a) 4
(b) 11
(c) 5
(d) 0
Answer
B
Question: Consider the system of linear equations
x1 +2x2 +x3=3
2x1+ 3x2+x3=3
3x1+5x2+2x3=1
The system has
(a) infinite number of solutions
(b) exactly 3 solutions
(c) a unique solution
(d) no solution
Answer
C
Question: The number of 3 x3 non-singular matrices, with four entries as 1 and all other entries as 0, is
(a) less than 4
(b) 5
(c) 6
(d) at least 7
Answer
D
Question:

Answer
D
Question: Let A be a square matrix all of whose entries are integers. Then, which one of the following is true?
(a) If det (A )= ± 1, then A-1 need not exist
(b) If det (A) = ± 1, then A-1exists but all its entries are not necessarily integers
(c) If det ( A) ≠ ± 1, then A-1 exists and all its entries are non-integers
(d) If det (A) = ± 1, then A-1 exists and all its entries are integers
Answer
D
Question: If A and B are 3x 3 matrices such that A2– B2=(A-B) (A+B), then
(a) either A or B is zero matrix
(b) either A or B is unit matrix
(c) A =B
(d) AB = BA
Answer
D
Question: Let A =

If det (A2)= 25 ,then| α| is
(a) 1
(b) 1/5
(c) 5
(d) 52
Answer
B
Question. If A

, then A + A’ = I, if the value of α is
(a) π/6
(b) π/3
(c) π
(d) 3π/2
Answer
B
Question .If A and B are symmetric matrices of the same order, then (AB’ – BA’) is a
(a) Skew symmetric matrix
(b) Null matrix
(c) Symmetric matrix
(d) None of these
Answer
A
Question. If A and B are square matrices of the same order, then (A + B)(A – B) is equal to
(a) A2 – B2
(b) A2 – BA – AB – B2
(c) A2 – B2 + BA – AB
(d) A2 – BA + B2 + AB
Answer
C
Question .Total number of possible matrices of order 3 × 3 with each entry 2 or 0 is
(a) 9
(b) 27
(c) 81
(d) 512
Answer
D
Question. The matrix
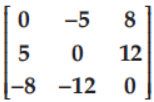
is a
(a) diagonal matrix
(b) symmetric matrix
(c) skew symmetric matrix
(d) scalar matrix
Answer
C
Question. The matrix

(a) a skew-symmetric matrix
(b) a symmetric matrix
(c) a diagonal matrix
(d) an upper triangular matrix.
Answer
A
Question. If

(a) x = 3, y = 1
(b) x = 2, y = 3
(c) x = 2, y = 4
(d) x = 3, y = 3
Answer
B
Question. If the matrix AB is zero, then
(a) It is not necessary that either A = O or B = O
(b) A = O or B = O
(c) A = O and B = O
(d) All the statements are wrong
Answer
A
Question. If n = p, then the order of the matrix 7X – 5Z is
(a) p × 2
(b) 2 × n
(c) n × 3
(d) p × n
Answer
b
Question. If A and B are matrices of same order, then (AB’ – BA’) is a [NCERT Exemplar]
(a) skew-symmetric matrix
(b) null matrix
(c) symmetric matrix
(d) unit matrix
Answer
a
Question. If A and B are two matrices of the order 3 × m and 3 × n respectively and m = n, then the order of matrix (5A – 2B) is
(a) m × 3
(b) 3 × 3
(c) m × n
(d) 3 × n
Answer
d
Question. The restriction on n, k and p so that PY + WY will be defined are
(a) k = 3, p = n
(b) k is arbitrary, p = 2
(c) p is arbitrary, k = 3
(d) k = 2, p = 3
Answer
A
Question. If A is square matrix such that A2 = I, then (A – I)3 + (A + I)3 –7A is equal to
(a) A
(b) I – A
(c) I + A
(d) 3A
Answer
A
Question . If A is matrix of order m × n and B is a matrix such that AB’ and B’A are both defined, the order of matrix B is
(a) m × m
(b) n × n
(c) n × m
(d) m × n
Answer
D
Question. If A =
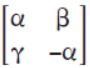
is such that A2 = I, then
(a) 1 + a2 + bc = 0
(b) 1 – a2 + bc = 0
(c) 1– a2 – bc = 0
(d) 1 + a2– bc = 0
Answer
C
Question. If A =

(a) only AB is defined
(b) only BA is defined
(c) AB and BA both are defined
(d) AB and BA both are not defined.
Answer
C
Question. If A =
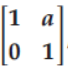
then An (where n∈N) equals

Answer
A
Question. If A =
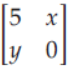
and A = Al , then
(a) x = 0, y = 5
(b) x + y = 5
(c) x = y
(d) none of these
Answer
C
Question. A matrix which is not a square matrix is called a _ matrix.
Answer
rectangular
Question. If A and B are square matrix of the same order then (AB)l = _
Answer
B’ A’
Question. If A is a skew-symmetric matrix and n∈N such that (An)T = mAn then l= __ .
Answer
(–1)n
A and B are two matrices of same order 3×3, where

Question: The value of |adj (adj A) is equal to
(a) 9
(b) 1
(c) 25
(d) 81
Answer
B
Question: The value of | adj (B)| is equal to
(a) 24
(b) 242
(c) 243
(d) 82
Answer
B
Question: The value of adj (adj A) is equal to
(a) -A
(b) 4 A
(c) 8A
(d) 16 A
Answer
A
Question: The value of |(adj (adj (adj (adj A)))) is equal to
(a) 24
(b) 29
(c) 1
(d) 219
Answer
B
Question: The value of |adj (AB)| is equal to
(a) 24
(b) 242
(c) 243
(d) 65
Answer
B
Question. Which of the following is correct statement?
(a) Diagonal matrix is also a scalar matrix
(b) Identity matrix is a particular case of scalar matrix
(c) Scalar matrix is not a diagonal matrix
(d) Null matrix cannot be a square matrix
Answer
B
Question.
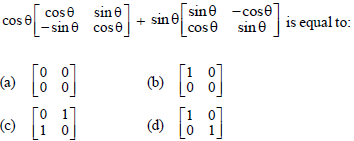
Answer
D
Question. If the matrices A = [aij] and B = [bji] and C = [cji] are of the same order, say m × n, satisfy Associative law, then
(a) (A + B) + C = A + (B + C)
(b) A + B = B + C
(c) A + C = B + C
(d) A + B + C = A – B – C
Answer
A
Question. Match the terms given in column-I with the terms given in column-II and choose the correct option from the codes given below.

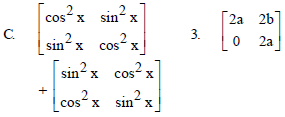
Codes
A B C
(a) 3 1 2
(b) 1 3 2
(c) 2 1 3
(d) 3 2 1
Answer
A
Question.

(a) AAT = I
(b) BBT = I
(c) AB ≠ BA
(d) (AB)T = I
Answer
D
Question. If a matrix A is both symmetric and skew-symmetric, then
(a) A is a diagonal matrix
(b) A is zero matrix
(c) A is a scalar matrix
(d) A is square matrix
Answer
B
Question. If matrix A = [aij]2 × 2, where
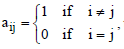
then A2 is equal to
(a) I
(b) A
(c) O
(d) None of these
Answer
A
Question. If a matrix has 8 elements, then which of the following will not be a possible order of the matrix?
(a) 1 × 8
(b) 2 × 4
(c) 4 × 2
(d) 4 × 4
Answer
D
Question.
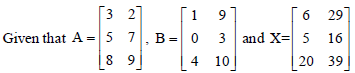
and if 2A + 6B = kX, then the value of k is
(a) 2
(b) 3
(c) 4
(d) 5
Answer
A
Question.
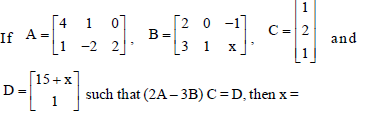
(a) 3
(b) – 4
(c) – 6
(d) 6
Answer
C
Question.

(a) −1/2
(b) 1/2
(c) 1
(d) – 1
Answer
B
Question. If X, A and B are matrices of the same order such that X = AB, then we apply elementary column transformation simultaneously on X and on the matrix
(a) B
(b) A
(c) AB
(d) Both A and B
Answer
A
Question. The product of two matrices A and B is defined, if the number of columns of A is
(a) greater than the number of rows of B
(b) equal to the number of rows of B
(c) less than the number of rows of B
(d) None of the above
Answer
B
Question. If A = [aij]3 × 4 is matrix given by
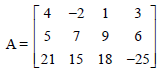
Then, a23 + a24 will be equal to the element
(a) a14
(b) a44
(c) a13
(d) a32
Answer
D
Question. If A is a square matrix, then A + AT is
(a) Non-singular matrix
(b) Symmetric matrix
(c) Skew-symmetric matrix
(d) Unit matrix
Answer
B
Assertion and Reason
Each of these questions contains two.
statements : Statement I (Assertion) and Statement II (Reason). Each of these questions also has four alternative choices, only one of which is the correct answer. You have to select one of the codes (a), (b), (c) and (d) given below.
(a) Statement I is true, Statement II is true; Statement II is a correct explanation for Statement I.
(b) Statement I is true, Statement II is true; Statement II is not a correct explanation for Statement I.
(c) Statement I is true; Statement II is false.
(d) Statement I is false; Statement II is true.
Question: Statement I If A is a skew-symmetric matrix of order 3 x 3, then det(A) = 0 or|A| = 0.
Statement II If A is square matrix, then det( A)= det(A’ ) =det(-A’)
Answer
B
Question: Statement I If a matrix of order2x 2, commutes with every matrix of order 2x 2, then it is scalar matrix.
Statement II A scalar matrix of order 2x 2commutes with every 2x 2 matrix.
Answer
A
Question: Statement I The inverse of A =
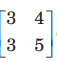
does not exist.
Statement II The matrix A is non-singular.
Answer
C
Question: Statement I The matrix A =1/3

is an orthogonal matrix.
Statement II If A and B are orthogonal, then AB is also orthogonal.
Answer
C
Question: Let A be a square matrix of order 3 satisfying AA’= I to
Statement I A’ A=1
Statement II (AB)’ =A’
Answer
B
Question: Statement I

is a diagonal matrix.
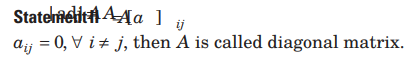
Answer
C
Question: Statement I If A =

then adj (adj A)=A.
Statement II |adj (adj A)|=|A |(n-1)2 , A be n rowed non-singular matrix.
Answer
C
Question: Statement I If A is a matrix of order 2x 2, then |adj A|= |A| because
Statement II |A|=| AT|
Answer
B
Question: Let A be a 2 2 ´ matrix with real entries. Let I be the 2 x2 identity matrix. Denote by Tr (A), the sum of diagonal entries of A. Assume that A2 =I.
Statement I If A ≠I and A ≠ -1,then det (A) = – 1
Statement II If A≠ I and A≠ -I, then Tr (A) ≠ 0
Answer
D
Question: Statement I If A =

and | A| = 0 because
Statement II The value of the determinant of a skew-symmetric matrix is zero.
Answer
A
Question:
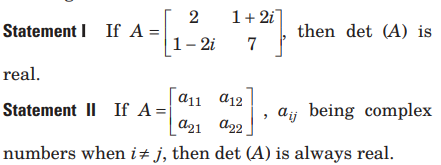
Answer
A
Question: Let A and B be two symmetric matrices of order 3.
Statement I A(BA) and (AB)A are symmetric matrices.
Statement II AB is symmetric matrix, if matrix multiplication of A with B is commutative.
Answer
C
Question: Let A be a 2x 2 matrix with non-zero entries and let A2=1, where I is 2x 2 identity matrix.
Define Tr(A) = sum of diagonal elements of A and |A | = determinant of matrix A.
Statement I Tr(A) = 0
Statement II |A| = 1
Answer
A
Question. If A and B are symmetric matrices of same order then AB is symmetric if and only if _____________ .
Answer
AB = BA
Question. If A is symmetric matrix, then BlAB is _____________ .
Answer
Symmetric Matrix

We hope the above multiple choice questions for Class 12 Mathematics for Chapter 3 Matrices provided above with answers based on the latest syllabus and examination guidelines issued by CBSE, NCERT and KVS are really useful for you. Matrices is an important chapter in Class 12 as it provides very strong understanding about this topic. Students should go through the answers provided for the MCQs after they have themselves solved the questions. All MCQs have been provided with four options for the students to solve. These questions are really useful for benefit of class 12 students. Please go through these and let us know if you have any feedback in the comments section.
