MCQs for Mathematics Class 12 with Answers Chapter 5 Continuity and Differentiability
Students of class 12 Mathematics should refer to MCQ Questions Class 12 Mathematics Continuity and Differentiability with answers provided here which is an important chapter in Class 12 Mathematics NCERT textbook. These MCQ for Class 12 Mathematics with Answers have been prepared based on the latest CBSE and NCERT syllabus and examination guidelines for Class 12 Mathematics. The following MCQs can help you to practice and get better marks in the upcoming class 12 Mathematics examination
Chapter 5 Continuity and Differentiability MCQ with Answers Class 12 Mathematics
MCQ Questions Class 12 Mathematics Continuity and Differentiability provided below have been prepared by expert teachers of grade 12. These objective questions with solutions are expected to come in the upcoming Standard 12 examinations. Learn the below provided MCQ questions to get better marks in examinations.
Question. The function f (x) = e x is
(a) continuous everywhere but not differentiable at x = 0
(b) continuous and differentiable everywhere
(c) not continuous at x = 0
(d) none of these
Answer
A
Question. A function f (x) is defined as f (x) = A sin x + sin 2x/x3,(x≠ 0).
If the function is continuous at x = 0, then
(a) A = − 2
(b )f(0) =-1
(c) A = 1
(d) f(0) = 1
Answer
(A.C)
Question. If f(x)=|log x |, then
(a) f′(1+)=1
(b) f′ (1-) = -1
(c) f′ =(1) = 1
(d) f′(1) = -1
Answer
(A,B)
Question.
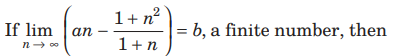
(a) a = 1
(b) a = 0
(c) b = 1
(d) b = −1
Answer
(A,C)
Question. If f(x=x3 sgn (x), then
(a) f is differentiable at x = 0
(b) f is continuous but not differentiable at x = 0
(c) f′ (0+) = 0
(d) f′(0-) =1
Answer
(A,C)
Question. f (x) is differentiable function and [f(x)·g (x)] is differentiable at x= a, then
(a) g (x) must be differentiable at x a =
(b) if g (x) is discontinuous, then f(a) = 0
(c) f (a)≠ 0, then g(x) must be differentiable
(d) nothing can be said
Answer
(B.C)
Question. The function y = sin-1 (cos x) is not differentiable at
(a) x = π
(b) x = − 2π
(c) x = 2π
(d) x = π/2
Answer
(A,B,C)
Question. The set of points where the function f (x) =x/(1+ |x| is differentiable, is
(a) (−∞ ∞, )
(b) [0, ∞)
(c) (−∞, 0) ∪ (0,∞)
(d) (0,∞)
Answer
(A,B,C,D)
Question. If x+|y|2y,then y as a function of x is
(a) defined for all real x
(b) continuous at x = 0
(c) differentiable for all x
(d) such that dy/dx= 1/3 for x<0
Answer
(A,B,D)
Question.
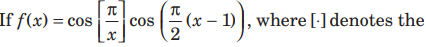
greatest integer function, then f (x) is continuous at
(a) x = 0
(b) x = 1
(c) x = 2
(d) None of these
Answer
(B,C)
Question. If f (x) = min {1,x2,x3}, = then
(a) f (x) is continuous everywhere
(b) f (x) is continuous and differentiable everywhere
(c) f (x) is not and differentiable at two points
(d) f (x) is not differentiable at one point
Answer
(A,D)
Question.
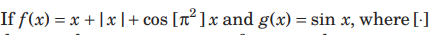
denotes the greatest integer function, then
(a) f (x)+ g (x) is continuous everywhere
(b) f (x)+g (x) is differentiable everywhere
(c) f (x)+ g (x) is differentiable everywhere
(d) f (x)+g (x )is continuous but not differentiable at x = 0
Answer
(A,C)
Question.

(a) a = −7
(b) a +b = 0
(c) b+ c = 2
(d) b- c = 12
Answer
(A,B,C,D)
Question.
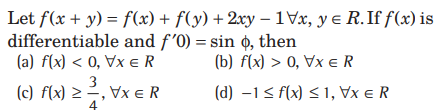
Answer
(B.C)
Question. Let h(x) min { x,x2} for every real number x. Then,
(a) h is continuous for all x
(b) h is differentiable for all x
(c) h′(x)=1 for all x>1
(d) h is not differentiable at two values of x
Answer
(A.C.D)
Question. If f (x)= min(tan x, cot x),then
(a) f (x) is discontinuous at x = 0,π/4 and 5π/4
(b) f (x) is continuous at x = π/2 and 3π/2

(d) f (x) is periodic with period π )
Answer
(C.D)
Question.

λ is
(a) −2
(b) −1
(c) 1
(d) 2
Answer
(B.D)
Question.
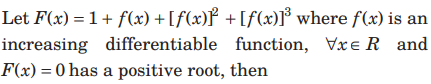
(a) F (x) is an increasing function
(b) F(0) < 0
(c) f(0) < −
(d) F'(0)> 0
Answer
(A,B,C,D)
Question:
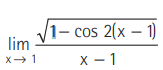
(a) exists and it equals √2
(b) exists and it equals − √2
(c) does not exists
(d) None of these
Answer
C
Question:
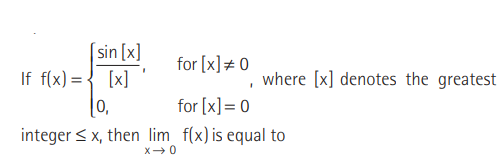
(a) 1
(b) 0
(c) −1
(d) None of these
Answer
D
Question

(a) 2
(b) 3
(c) 5
(d) None of these
Answer
C
Question:

(a) 1/2
(b) 0
(c) 1
(d) None of these
Answer
A
Question:
(a) 0
(b) 3/ 5
(c) 1
(d) None of these
Answer
A
Question:
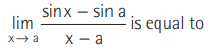
(a) sin a
(b) 0
(c) cos a
(d) None of these
Answer
C
Question
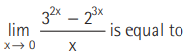
(a) log 3/ 2
(b) 1
(c) log 9/ 8
(d) 0
Answer
C
Question:

(a) 2
(b) −2
(c) 1
(d) 0
Answer
B
Question
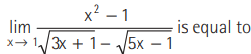
(a) 4
(b) −4
(c) 2
(d) None of these
Answer
B
Question: if (x) =x(√x +√x+1), then
(a) f (x ) is continuous but not differentiable at x = 0
(b) f (x ) is differentiable at x = 0
(c) f ( x) is not differentiable at x = 0
(d) None of the above
Answer
B
Question:
(a) a = 0
(b) a = 1
(c) a = − 1
(d) None of these
Answer
A
Question: The set of all points where the function f(x) = x/1+| x| is differentiable, is
(a) ( −∞, ∞)
(b) [0, ∞)
(c) ( − ∞, 0) ∪ (0,∞)
(d) (0,∞)
Answer
A
Question: For a real number y, let[ y] denotes the greatest integer less than or equal to y, then the function f (x)
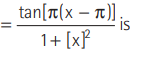
(a) discontinuous at some x
(b) continuous at all x but the derivative f′(x) does not exist for some x
(c) f′( x) exists ∀ x but f′′( x) does not exist for some x
(d) f′′(x ) exists for all x
Answer
D
Question: If f (x) = acos x -cos bx/x2,x≠0 and f(0)=4 is continuous at x = 0, then the ordered pair( a, b) is
(a) ( ± 1, 3)
(b) (1, ± 3)
(c) (-1,-3)
(d) (1,3)
Answer
B
Question
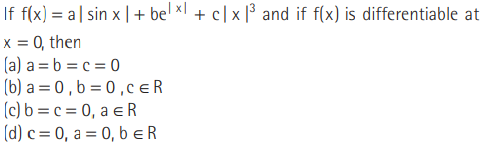
Answer
B
Question:
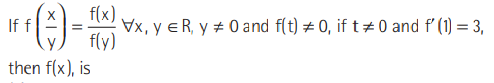
(a) x
(b) x2
(c) x3
(d) Constant
Answer
C
Question: The set of points where the function f (x)=√1-e-x2 is differentiable, is
(a) ( −∞, ∞)
(b) (− ∞,0)∪ (0,∞)
(c) (-1,∞)
(d) None of these
Answer
B
Question

Answer
B
Question: Let f (x +y) = f (x) f(y), ∀ x, y ∈ R, f(5)=2, f′(0 )= 3, then f'(5) equals
(a) 6
(b) 3
(c) 5
(d) None of these
Answer
A
Question: The value o

(a) 10/3
(b) 3/10
(c) 6/5
(d) 5/6
Answer
A
Question:

(a) 0
(b) e
(c) 1 e
(d) 1
Answer
D
Question:

(a) 0
(b) 1
(c) 10
(d) 100
Answer
D
Question:
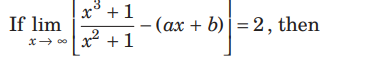
(a) a = 1and b = 1
(b) a = 1and b = − 1
(c) a = 1and b = − 2
(d) a = 1and b = 2
Answer
C
Question:
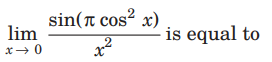
(a) − π
(b) π
(c) π /2
(d) 1
Answer
B
Question:
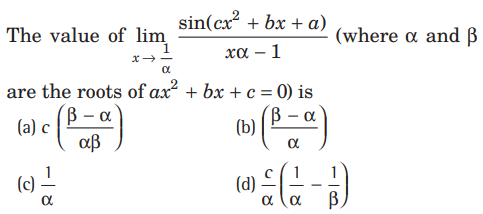
Answer
D
Question:
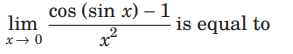
(a) 1
(b) − 1
(c) 1/2
(d) −/12
Answer
B
Question

(a) e
(b) e2
(c)e−1
(d) 1
Answer
B
Question: The integer n for which
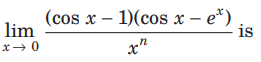
a finite non-zero number, is
(a) 1
(b) 2
(c) 3
(d) 4
Answer
D
Question. The function f (x) = 4-x2 /4x-x3 is
(a) discontinuous at only one point
(b) discontinuous at exactly two points
(c) discontinuous at exactly three points
(d) none of these
Answer
C
Question. The number of points at which the function f (x) = 1/x-[x] is not continuous is
(a) 1
(b) 2
(c) 3
(d) none of these
Answer
D
Question. The value of c in Rolle’s theorem for the function f(x) = x3 – 3x in the interval [0, 3] is
(a) 1
(b) –1
(c) 3/2
(d) 1/3
Answer
A
Question. Let f (x) = sinx . Then
(a) f is everywhere differentiable
(b) f is everywhere continuos but not differentiable at x = nπ : n ∈ Z
(c) f is everywhere continuous but not differentiable at x (2n + 1)π/2 , n ∈ Z
(d) none of these
Answer
B
Question. If f (x) x sin 1/x, where x ! 0 , then the value of the function f at x = 0, so that the function is continuous at x = 0, is
(a) 0
(b) –1
(c) 1
(d) None of these
Answer
A
Question. The function f(x) = |x| + |x – 1| is
(a) continuous at x = 0 as well as at x = 1.
(b) continuous at x = 1 but not at x = 0.
(c) discontinuous at x = 0 as well as at x = 1.
(d) continuous at x = 0 but not at x = 1.
Answer
A
Question. The value of c in Rolle’s Theorem for the function f(x) = ex sin x, in [0, π] is
(a) π/6
(b) π/4
(c) π/2
(d) 3π/4
Answer
D
Question. The function f : R → R given by f(x) = – |x – 1| is [CBSE 2020 (65/2/1)]
(a) continuous as well as differentiable at x = 1
(b) not continuous but differentiable at x = 1
(c) continuous but not differentiable at x = 1
(d) neither continuous nor differentiable at x = 1
Answer
C
Question. The value of c in Mean Value Theorem for the function f(x) = x(x – 2), x ∈ [1, 2] is
(a) 3/2
(b) 2/3
(c) 1/2
(d) 7/4
Answer
A
Question. The function f(x) = [x], where [x] denotes the greatest integer function, is continuous at
(a) 4
(b) –2
(c) 1
(d) 1.5
Answer
D
Question. Differential coefficient of sec (tan–1x) w.r.t. x is
(a) x/√(1+x2)
(b) x/(1+x2)
(c) x/(1+x2)
(d) 1/√(1+x2)
Answer
A
Question. The function (x) =x-1/x(x2-1) is discontinuous at
(a) exactly one point
(b) exactly two points
(c) exactly three points
(d) no point
Answer
C
Question. If u sin-1 (2x/1+x2) and v tan-1 (2x/1-x2) , then du/dv is
(a) 1/2
(b) x
(c) 1-x2/1+x2[4, -4]Φ
(d) 1
Answer
D
Question. If y = log tanx , then the value of dy/dx at x = π/4 is
(a) 0
(b) 1
(c) 1/2
(d) ∞
Answer
B
Question. The set of points where the functions f given by f (x) = |x – 3| cos x is differentiable is
(a) R
(b) R – {3}
(c) (0, ∞)
(d) none of these
Answer
B
Choose and write the correct option in each of the following questions.
Question. If f(x) = 2x and g(x) = x2/2 + 1 , then which of the following can be a discontinuous function?
(a) f(x) + g(x)
(b) f(x) – g(x)
(c) f(x) . g(x)
(d) g(x)/ f(x )
Answer
D
Question. If y = A e5x + B e–5x, then d2y/dx2 is equal to
(a) 25 y
(b) 5 y
(c) –25 y
(d) 15 y
Answer
A
Question. For the curve √x + √y =1 ,dy/dx , at(1/4 ,1/4) is
(a) 1/2
(b) 1
(c) –1
(d) 2
Answer
C
Question. If f ′(1) = 2 and y = f (log ex), then dy/dx at x = e is
(a) 0
(b) 1
(c) e
(d) 2/e
Answer
D
(i) If f (x) = cos x , then f (π/4) = _____________ .
Answer
-1/√2
(ii) If f(x) = (x + 1), then (d/dx) fof (x) = _____________ .
Answer
1
(iii) d/dx sec(tan-1)= _____________ .
Answer
x/√1 + x2
(iv) The number of points at which the function f(x)=1/log|x| is discontinuous is _________ .
Answer
three
Question. If y = tan–1 x + cot–1 x, x ∈ R, then dy/dx is equal to _____________ .
Answer
0
Question. The function f (x) = 2 -X2 /9X – X3 is discontinuous exactly at _____________ points.
Answer
three
Question. If cos (xy) = k, where k is a constant and xy ≠ np, n ∈ Z, then dy/dx is equal to _____________ .
Answer
-y/x
Question. The number of points of discontinuity of f defined by f(x) = |x| – |x + 1| is _____________.
Answer
0
if f(x +y) = f(x) + (y) for all
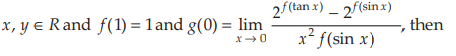
On the basis of above information, answer the following questions.
Question. The value of f(x) is
(a) x
(b) x2
(c) 3x
(d) None of these A
Question. The value of g(0) is

Answer
B
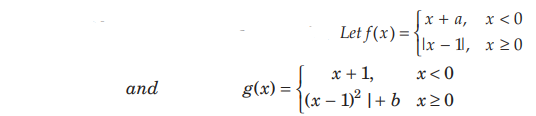
where, a b and are non-negative real numbers. On the basis of above information, answer the following questions
Question. The value of a, if(gof) x is continuous for all real x, is
(a) –1
(b) 0
(c) 1
(d) 2
Answer
C
Question. The value of b, if go f (x) is continuous for all real x, is
(a) –1
(b) 0
(c) 1
(d) 2
Answer
B

We hope the above multiple choice questions for Class 12 Mathematics for Chapter 5 Continuity and Differentiability provided above with answers based on the latest syllabus and examination guidelines issued by CBSE, NCERT and KVS are really useful for you. Continuity and Differentiability is an important chapter in Class 12 as it provides very strong understanding about this topic. Students should go through the answers provided for the MCQs after they have themselves solved the questions. All MCQs have been provided with four options for the students to solve. These questions are really useful for benefit of class 12 students. Please go through these and let us know if you have any feedback in the comments section.
