MCQs for Physics Class 11 with Answers Chapter 7 Systems of Particles and Rotational Motion
Students of class 11 Physics should refer to MCQ Questions Class 11 Physics Systems of Particles and Rotational Motion with answers provided here which is an important chapter in Class 11 Physics NCERT textbook. These MCQ for Class 11 Physics with Answers have been prepared based on the latest CBSE and NCERT syllabus and examination guidelines for Class 11 Physics. The following MCQs can help you to practice and get better marks in the upcoming class 11 Physics examination
Chapter 7 Systems of Particles and Rotational Motion MCQ with Answers Class 11 Physics
MCQ Questions Class 11 Physics Systems of Particles and Rotational Motion provided below have been prepared by expert teachers of grade 11. These objective questions with solutions are expected to come in the upcoming Standard 11 examinations. Learn the below provided MCQ questions to get better marks in examinations.
Question. A wheel is rolling straight on ground without slipping. If the axis of the wheel has speed v, the instantenous velocity of a point P on the rim, defined by angle q, relative to the ground will be
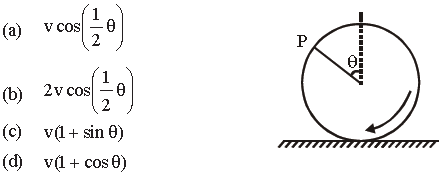
Answer
B
Question. The wheel of a car is rotating at the rate of 1200 revolutions per minute. On pressing the accelerator for 10 seconds it starts rotating at 4500 revolutions per minute. The angular acceleration of the wheel is
(a) 30 radian / second2
(b) 1880 degrees/ second2
(c) 40 radian / second2
(d) 1980 degree/second2
Answer
D
Question. Acertain bicycle can go up a gentle incline with constant speed when the frictional force of ground pushing the rear wheel is F2 = 4 N. With what force F1 must the chain pull on the sprocket wheel if R1=5 cm and R2 = 30 cm?

(a) 4 N
(b) 24 N
(c) 140 N
(d) (35/4) N
Answer
B
Question. Auniform rod of length l is free to rotate in a vertical plane about a fixed horizontal axis through O. The rod begins rotating from rest from its unstable equilibrium position. When it has turned through an angle q, its angular velocity w is given as

Answer
C
Question. Five masses are placed in a plane as shown in figure. The coordinates of the centre of mass are nearest to
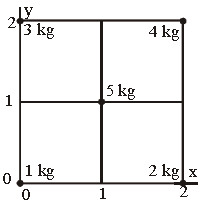
(a) 1.2, 1.4
(b) 1.3, 1.1
(c) 1.1, 1.3
(d) 1.0, 1.0
Answer
C
Question. A solid sphere of mass 1 kg rolls on a table with linear speed 1 ms–1. Its total kinetic energy is
(a) 1 J
(b) 0.5 J
(c) 0.7 J
(d) 1.4 J
Answer
C
Question. A sphere of mass 2000 g and radius 5 cm is rotating at the rate of 300 rpm .Then the torque required to stop it in 2p revolutions, is
(a) 1.6 × 102 dyne cm
(b) 1.6 × 103 dyne cm
(c) 2.5 × 104 dyne cm
(d) 2.5 × 105 dyne cm
Answer
D
Question. A solid sphere of mass M and radius R is pulled horizontally on a sufficiently rough surface as shown in the figure.

Choose the correct alternative.
(a) The acceleration of the centre of mass is F/M
(b) The acceleration of the centre of mass is 2 F/3 M
(c) The friction force on the sphere acts forward
(d) The magnitude of the friction force is F/3
Answer
B, C
Question. M.I of a circular loop of radius R about the axis in figure is
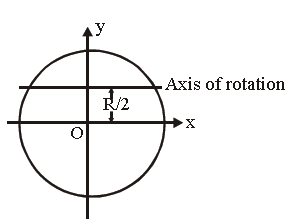
(a) MR2
(b) (3/4) MR2
(c) MR2/2
(d) 2MR2
Answer
B
Question. A boy and a man carry a uniform rod of length L, horizontally in such a way that the boy gets 1/4th load. If the boy is at one end of the rod, the distance of the man from the other end is
(a) L/3
(b) L/4
(c) 2 L/3
(d) 3 L/4
Answer
A
Question. If the earth is treated as a sphere of radius R and mass M, its angular momentum about the axis of its diurnal rotation with period T is
(a) 4πMR2/5T
(b) 2πMR2/5T
(c) MR2T/T
(d) πMR3/T
Answer
A
Question. Four masses are fixed on a massless rod as shown in the adjoining figure. The moment of inertia about the dotted axis is about

(a) 2 kg × m2
(b) 1 kg × m2
(c) 0.5 kg × m2
(d) 0.3 kg × m2
Answer
B
Question. A round disc of moment of inertia I2 about its axis perpendicular to its plane and passing through its centre is placed over another disc of moment of inertia I1 rotating with an angular velocity w about the same axis. The final angular velocity of the combination of discs is

Answer
D
Question. In a bicycle, the radius of rear wheel is twice the radius of front wheel. If rF and rF are the radii, vr and vr are the speed of top most points of wheel. Then
(a) vr = 2vF
(b) vF = 2vr
(c) vF = vr
(d) vF > vr
Answer
C
Question. Three particles, each of mass m gram, are situated at the vertices of an equilateral triangle ABC of side/cm (as shown in the figure). The moment of inertia of the system about a line AX perpendicular to AB and in the plane of ABC, in gram-cm2 units will be

Answer
D
Question. Two bodies have their moments of inertia I and 2I respectively about their axis of rotation. If their kinetic energies of rotation are equal, their angular momenta will be in the ratio
(a) 2 : 1
(b) 1 : 2
(c) √2 : 1
(d) 1 : √2
Answer
D
Question. A wheel having moment of inertia 2 kg-m2 about its vertical axis, rotates at the rate of 60 rpm about this axis, The torque which can stop the wheel’s rotation in one minute would be
(a) (π/18) Nm
(b) (2π/15 Nm
(c) (π/12) Nm
(d) (π/15) Nm
Answer
D
Question. A drum of radius R and mass M, rolls down without slipping along an inclined plane of angle q. The frictional force
(a) dissipates energy as heat.
(b) decreases the rotational motion.
(c) decreases the rotational and translational motion.
(d) converts translational energy to rotational energy
Answer
D
Question. From a disc of radius R and mass M, a circular hole of diameter R, whose rim passes through the centre is cut. What is the moment of inertia of the remaining part of the disc about a perpendicular axis, passing through the centre ?
(a) 15 MR2/32
(b) 13 MR2/32
(c) 11 MR2/32
(d) 9 MR2/32
Answer
B
Question. A tube of length L is filled completely with an incompressible liquid of mass M and closed at both ends. The tube is then rotated in a horizontal plane about one of its ends with uniform angular speed w. What is the force exerted by the liquid at the other end?
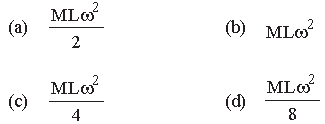
Answer
A
Question. A circular disk of moment of inertia It is rotating in a horizontal plane, its symmetry axis, with a constant angular speed ϖi . Another disk of moment of inertia Ib is dropped coaxially onto the rotating disk. Initially the second disk has zero angular speed. Eventually both the disks rotate with a constant angular speed ϖf . The energy lost by the initially rotating disk to friction is

Answer
D
Question. The moment of inertia of a uniform circular disc of radius ‘R’ and mass ‘M’ about an axis passing from the edge of the disc and normal to the disc is

Answer
C
Question. The moment of inertia of a thin uniform rod of mass M and length L about an axis passing through its midpoint and perpendicular to its length is I0. Its moment of inertia about an axis passing through one of its ends and perpendicular to its length is
(a) I0 + ML2/2
(b) I0 + ML2/4
(c) I0 + 2ML2
(d) I0 + ML2
Answer
B
Question. The ratio of the radii of gyration of a circular disc about a tangential axis in the plane of the disc and of a circular ring of the same radius about a tangential axis in the plane of the ring is
(a) 1 : √2
(b) 1 : 3
(c) 2 : 1
(d) √5 : √6
Answer
D
Question. Three masses are placed on the x-axis : 300 g at origin, 500 g at x = 40 cm and 400 g at x = 70 cm. The distance of the centre of mass from the origin is
(a) 40 cm
(b) 45 cm
(c) 50 cm
(d) 30 cm
Answer
A
Question. The instantaneous angular position of a point on a rotating wheel is given by the equation θ (t) = 2t3 – 6t2. The torque on the wheel becomes zero at
(a) t = 1s
(b) t = 0.5 s
(c) t = 0.25 s
(d) t = 2s
Answer
A
Question. If the angular velocity of a body rotating about an axis is doubled and its moment of inertia halved, the rotational kinetic energy will change by a factor of :
(a) 4
(b) 2
(c) 1
(d) 2/1
Answer
B
Question. For which of the following does the centre of mass lie outside the body?
(a) A pencil
(b) A shotput
(c) A dice
(d) A bangle
Answer
D
Question. The moment of inertia of a uniform circular disc is maximum about an axis perpendicular to the disc and passing through

(a) B
(b) C
(c) D
(d) A
Answer
A
Question. Which of the following points is the likely position of the centre of mass of the system shown in figure?
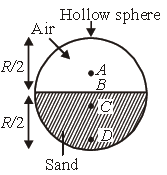
(a) A
(b) B
(c) C
(d) D
Answer
C
Question. A uniform square plate has a small piece Q of an irregular shape removed and glued to the centre of the plate leaving a hole behind in figure. The moment of inertia about the zaxis is then,
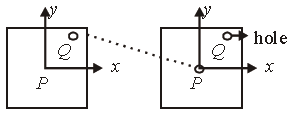
(a) increased
(b) decreased
(c) the same
(d) changed in unpredicted manner
Answer
B
Question. One quarter sector is cut from a uniform circular disc of radius R. This sector has mass M. It is made to rotate about a line perpendicular to its plane and passing through the centre of the original disc. Its moment of inertia about the axis of rotation is

Answer
A
Question. In problem-5, the CM of the plate is now in the following quadrant of x-y plane.
(a) I
(b) II
(c) III
(d) IV
Answer
C
Question. A merry-go-round, made of a ring-like platform of radius R and mass M, is revolving with angular speed w. A person of mass M is standing on it. At one instant, the person jumps off the round, radially away from the centre of the round (as seen from the round). The speed of the round of afterwards is
(a) 2ϖ
(b) ϖ
(c) ϖ/2
(d) 0
Answer
A
Question. A small object of uniform density rolls up a curved surface with an initial velocity ‘n’. It reaches upto a maximum height of 3v2/4g with respect to the initial position. The object is a
(a) solid sphere
(b) hollow sphere
(c) disc
(d) ring
Answer
C
Question. When a disc rotates with uniform angular velocity, which of the following is not true?
(a) The sense of rotation remains same
(b) The orientation of the axis of rotation remains same
(c) The speed of rotation is non-zero and remains same
(d) The angular acceleration is non-zero and remains same
Answer
D
Question. A rod PQ of mass M and length L is hinged at end P. The rod is kept horizontal by a massless string tied to point Q as shown in figure. When string is cut, the initial angular acceleration of the rod is

(a) g /L
(b) 2g/L
(c) 2g/3L
(d) 3g/2L
Answer
D
Question. The ratio of radii of gyration of a circular ring and a circular disc, of the same mass and radius, about an axis passing through their centres and perpendicular to their planes are
(a) 2 :1
(b) 1: 2
(c) 3 : 2
(d) 2 : 1
Answer
A
Question. The ratio of the accelerations for a solid sphere (mass ‘m’ and radius ‘R’) rolling down an incline of angle ‘θ’ without slipping and slipping down the incline without rolling is :
(a) 5 : 7
(b) 2 : 3
(c) 2 : 5
(d) 7 : 5
Answer
A
Question. A rod of weight W is supported by two parallel knife edges A and B and is in equilibrium in a horizontal position. The knives are at a distance d from each other. The centre of mass of the rod is at distance x from A. The normal reaction on A is
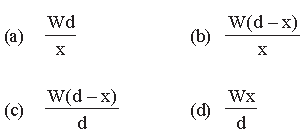
Answer
C
Question. A mass m moves in a circle on a smooth horizontal plane with velocity v0 at a radius R0. The mass is attached to string which passes through a smooth hole in the plane as shown.
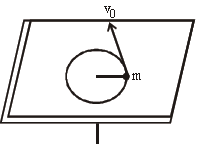
The tension in the string is increased gradually and finally m moves in a circle of radius R0/2 . The final value of the kinetic energy is

Answer
B
Question. Two discs are rotating about their axes, normal to the discs and passing through the centres of the discs. Disc D1 has 2 kg mass and 0.2 m radius and initial angular velocity of 50 rad s–1. Disc D2 has 4kg mass, 0.1 m radius and initial angular velocity of 200 rad s–1. The two discs are brought in contact face to face, with their axes of rotation coincident. The final angular velocity (in rad s–1) of the system is
(a) 40
(b) 60
(c) 100
(d) 120
Answer
C
Question. Point masses m1 and m2 are placed at the opposite ends of a rigid rod of length L, and negligible mass. The rod is to be set rotating about an axis perpendicular to it. The position of point P on this rod through which the axis should pass so that the work required to set the rod rotating with angular velocity ϖ0 is minimum, is given by :
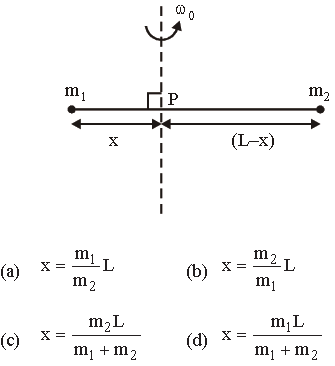
Answer
C
Question. A solid cylinder of mass 50 kg and radius 0.5 m is free to rotate about the horizontal axis. A massless string is wound round the cylinder with one end attached to it and other hanging freely. Tension in the string required to produce an angular acceleration of 2 revolutions s–2 is :
(a) 25 N
(b) 50 N
(c) 78.5 N
(d) 157 N
Answer
D
Question. An automobile moves on a road with a speed of 54 km h-1. The radius of its wheels is 0.45 m and the moment of inertia of the wheel about its axis of rotation is 3 kg m2. If the vehicle is brought to rest in 15s, the magnitude of average torque transmitted by its brakes to the wheel is :
(a) 8.58 kg m2 s-2
(b) 10.86 kg m2 s-2
(c) 2.86 kg m2 s-2
(d) 6.66 kg m2 s-2
Answer
D
Question. A force F→ = aˆi + 3ˆj+ 6kˆ is acting at a point r↔ = 2iˆ – 6ˆj-12kˆ . The value of a for which angular momentum about origin is conserved is :
(a) 2
(b) zero
(c) 1
(d) –1
Answer
D
Question. A disk and a sphere of same radius but different masses roll off on two inclined planes of the same altitude and length. Which one of the two objects gets to the bottom of the plane first ?
(a) Disk
(b) Sphere
(c) Both reach at the same time
(d) Depends on their masses
Answer
B
Question. Which of the following statements are correct ?
(A) Centre of mass of a body always coincides with the centre of gravity of the body
(B) Centre of mass of a body is the point at which the total gravitational torque on the body is zero
(C) A couple on a body produce both translational and rotation motion in a body
(D) Mechanical advantage greater than one means that small effort can be used to lift a large load
(a) (A) and (B)
(b) (B) and (C)
(c) (C) and (D)
(d) (B) and (D)
Answer
D
Question. A rope is wound around a hollow cylinder of mass 3 kg and radius 40 cm. What is the angular acceleration of the cylinder if the rope is pulled with a force of 30 N ?
(a) 0.25 rad/s2
(b) 25 rad/s2
(c) 5 m/s2
(d) 25 m/s2
Answer
B
Question. A ball rolls without slipping. The radius of gyration of the ball about an axis passing through its centre of mass is K. If radius of the ball be R, then the fraction of total energy associated with its rotational energy will be
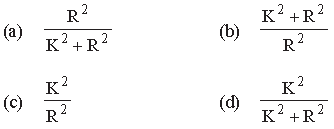
Answer
D

We hope the above multiple choice questions for Class 11 Physics for Chapter 7 Systems of Particles and Rotational Motion provided above with answers based on the latest syllabus and examination guidelines issued by CBSE, NCERT and KVS are really useful for you. Systems of Particles and Rotational Motion is an important chapter in Class 11 as it provides very strong understanding about this topic. Students should go through the answers provided for the MCQs after they have themselves solved the questions. All MCQs have been provided with four options for the students to solve. These questions are really useful for the benefits of class 11 students. Please go through these and let us know if you have any feedback in the comments section.
