Sample Paper Class 12 Mathematics Set L
1. If |z – i| ≤ 2 and z0 = 5 + 3i, then the maximum value of |iz + z0| is
(a) 2 + √31
(b) 7
(c) √31 − 2
(d) None of these
Answer
B
2. The continued product of four roots of

(a) 0
(b) 1
(c) i
(d) –1
Answer
B
3. If capital letters denote the cofactors of the corresponding small letters in

(a) Δ2
(b) 2Δ
(c) 0
(d) Δ
Answer
A
4.
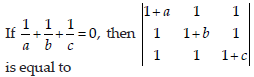
(a) – abc
(b) 0
(c) abc
(d) None of these
Answer
C
5.

Then x + y is equal to
(a) –1
(b) 1
(c) 6
(d) – 6
Answer
C
6. The position vectors of three points are 2a̅ − b̅ + 3c̅, a̅ − 2b̅ + mc̅ , and na̅ − 5b̅ where a̅ , b̅ , c̅ are non-coplanar vectors and m, n are scalars. The three points are collinear if and only if
(a) m = −2 n = 9/4
(b) m =9/4, n = − 2
(c) m = 2 n = 9/4
(d) m = −9/4, n = 2
Answer
B
7. If the vectors a̅ = î + ĵ + k̂ ,b̅ = 4î + 3ĵ + 4k̂ c̅= î + αĵ + βk̂ are linearly dependent and |c̅| = √3, then
(a) α = ±1, β = 1
(b) α = 1, β = –1
(c) α = 1, β = ±1
(d) α = –1, β = ±1
Answer
A
8. On each evening a boy either watches Doordarshan channel or Ten Sports. The probability that he watches Ten Sports is 4/5. If he watches Doordarshan, there is a chance of 3/4 that he will fall asleep, while it is 1/4 when he watches Ten Sports. On one day, the boy is found to be asleep. The probability that the boy watched Doordarshan is
(a) 5/7
(b) 2/7
(c) 3/7
(d) 4/7
Answer
C
9. Three groups A, B and C are competing for the positions on the Board of Directors of a company. The probabilities of their winning are 0.5, 0.3 and 0.2, respectively. If the group A wins, the probability of introducing a new product is 0.7 and other corresponding probabilites for groups B and C are, respectively, 0.6 and 0.5. The probability that new product will be introduced is
(a) 0.43
(b) 0.53
(c) 0.63
(d) 0.73
Answer
C
10. The range of random variable X is {1, 2, 3} and P(X = 1) = 3λ3, P(X = 2) = 4λ – 10λ2,
P(X = 3) = 5λ – 1 where l is constant. Then P(2 ≤ X ≤ 3) is equal to
(a) 8/9
(b) 2/3
(c) 4/9
(d) 1/3
Answer
A
11. In a book of 750 pages, there are 500 typographical errors. Assuming Poisson law for the number of errors per page, find the probability that a random sample of 5 pages will contain no error.
(a) e–10
(b) e–2/3
(c) e10
(d) e–10/3
Answer
D
12. The area enclosed within the curve |x| + |y| = 1 is
(a) 2
(b) 4
(c) 6
(d) none of these
Answer
A
13. The radius of the circle having centre at (2, 1), whose one of the chord is a diameter of the circle x2 + y2 – 2x – 6y + 6 = 0 is
(a) 1
(b) 2
(c) 3
(d) √3
Answer
C
14. The equation of the parobola whose focus is the point (0, 0) and the tangent at the vertex is x – y + 1 = 0 is
(a) x2 + y2 + 2xy – 4x – 4y + 4 = 0
(b) x2 + y2 – 2xy – 4x + 4y – 4 = 0
(c) x2 + y2 – 2xy + 4x – 4y – 4 = 0
(d) x2 + y2 + 2xy – 4x + 4y – 4 = 0
Answer
D
15. The angle between pair of tangents drawn to the ellipse 3x2 + 2y2 = 5 from the point (1, 2) is

Answer
C
16.

which of the following remains constant with change in ‘α’?
(a) abscissa of vertices
(b) abscissa of foci
(c) eccentricity
(d) directrix
Answer
B
17. Find the maximum value of f(x) = |x loge x| in (0, 1).
(a) e
(b) –e
(c) –1/e
(d) none of these
Answer
C
18. Semi-vertical angle of a cone is 45°. The height of cone is 30.05 cm. Find the approximate volume.
(a) 1325π c.c
(b) 9045π c.c
(c) 2020π c.c
(d) 330π c.c
Answer
B
19.
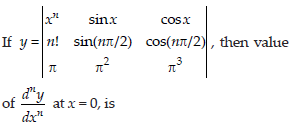
(a) 0
(b) π(π + 1)
(c) π2(π + 1)
(d) none of these
Answer
A
20.

Answer
A
21.
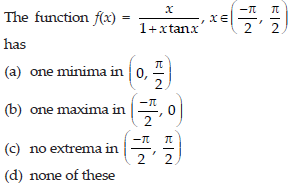
Answer
A, B
22. The function f(x) = (x – 1)m (x – 2)m+1 has
(a) inflection at x = 1, 2
(b) inflection at x = 1 or x = 2
(c) no point of inflection
(d) two points of extrema
Answer
B
23. Let Φ(x) = ∫x0g(t) dt, where g is such that
–1/2 ≤ g(t) ≤ 0 for t ∈ [0, 1]
–1/2 ≤ g(t) ≤ 1 for t ∈ [1, 3]
g(t) ≤ 1 for t ∈ [3, 4]
Then Φ(4) satisfies the inequality
(a) 1/2 ≤ Φ(4) ≤ 3
(b) 0 ≤ Φ(4) ≤ 2
(c) Φ(4) ≤ 3
(d) none of these
Answer
C
24. ∫0[x] ,[x]dx , is equal to
(a) [x]2 /2
(b) [x]([x]+ 1)/2
(c) [x]([x]− 1)/2
(d) ([x]− 1)([x]+ 1)/2
Answer
C
25. Find the shortest distance between the curves
y2 = x3 and 9x2 + 9y2 – 30y + 16 = 0.
(a) 0.5
(b) 0.2
(c) 1
(d) 3
Answer
B
26. The false statement in the following is
(a) (p ⇒ q) ⇔ (~ q ⇒ ~ p) is a contradiction
(b) ~ (~ p) ⇒ p is a tautotogy
(c) p ∨ (~ p) is a tautology
(d) p ∧ (~ p) is a contradiction
Answer
A
27. The inverse of the proposition (p ∧ ~ q) ⇒ r is
(a) ~ r ⇒ ~ p ∨ q
(b) r ⇒ p ∧ ~ q
(c) ~ p ∨ q ⇒ ~ r
(d) None of these
Answer
C
28. Which venn diagram represents the truth of the statement ‘No policeman is a thief’?
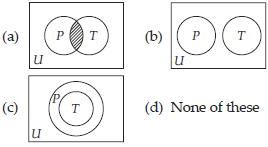
Answer
B
29. A line is uniquely determined if
(i) it passes through a given point and has given direction
(ii) it passes through two given points
(iii) it passes through a point and is parallel to a line.
(iv) it passes through two given points and is perpendicular to the plane
(a) only (i)
(b) (i) and (ii)
(c) (i), (ii) and (iii)
(d) all of these
Answer
D
30. If a, b, c are real numbers and planes
ax + by + cz = 0, bx + cy + az = 0, cx + ay + bz = 0 meet in a line then
(a) a2 + b2 + c2 = 0
(b) a2 + b2 + c2 = ab + bc + ca
(c) 3abc = a2 + b2 + c2
(d) 3( a2 + b2 + c2) = 2(ab + bc + ca)
Answer
B
31. The equation of the plane containing the
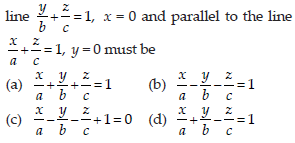
Answer
A
32. If π/2 < θ < 3π/2, the modulus and argument form of (1 + cos 2θ) + i sin 2θ is
(a) 2cos θ [cos θ + i sin θ]
(b) – 2cos θ [cos (π + θ) + i sin (π + θ)]
(c) 2cos θ [cos (– θ) + i sin (– θ)]
(d) – 2cos θ [cos (π – θ) + i sin (π – θ)]
Answer
B
33. The solution of the equation (x – h)2 + (y – k)2 = a2,where h and k are parameters’ is

Answer
B
34. The solution of the differential equation
(1 + y2)dx = (tan–1 y – x)dy is
(a) x = tan–1 y + 1 + Ce– tan–1 y
(b) y = tan–1 y + 1 + Ce– tan–1 y
(c) x = tan–1 y + Ce– tan–1 y
(d) None of these
Answer
D
35. The equation of the curve passing through the point (1,π/4) and having slope of tangent at any point (x, y) as y/x − cos2 y/x’ is
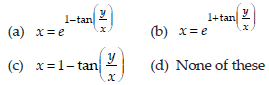
Answer
A
36. The area of the region bounded by the curves
y = 2x, y = 2x – x2 and x = 2, is
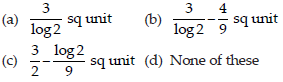
Answer
D
37.

Answer
A
38.
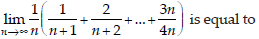
(a) log 4
(b) – log 4
(c) 1 – log 4
(d) None of these
Answer
D
39. ∫∞0e−x .x3 dx is equal to
(a) 0
(b) 2
(c) 6
(d) 9
Answer
C
40. The value of c from the Lagrange’s mean value theorem for which f(x) = √25 − x2 in [1, 5], is
(a) 5
(b) 1
(c) √15
(d) None of these
Answer
C
