Sample Paper Class 12 Mathematics Set N
1. If the system of linear equations
x – 2y + kz = 1,
2x + y + z = 2,
3x – y – kz = 3
has a solution (x, y, z), z ≠ 0, then (x, y) lies on the straight line whose equation is
(a) 3x – 4y – 4 = 0
(b) 3x – 4y – 1 = 0
(c) 4x – 3y – 4 = 0
(d) 4x – 3y – 1 = 0
Answer
C
2. The sum
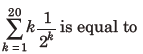
(a) 2-11/-219
(b) 1-11/-220
(c) 2-3/217
(d) 2-21/220
Answer
A
3. Let the numbers 2, b, c be in an AP
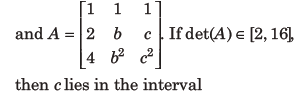
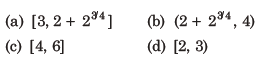
Answer
C
4.
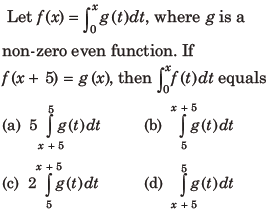
Answer
D
5. If the lengths of the sides of a triangle are in AP and the greatest angle is double the smallest, then a ratio of lengths of the sides of this triangle is
(a) 3 : 4 : 5
(b) 4 : 5 : 6
(c) 5 : 9 : 13
(d) 5 : 6 : 7
Answer
B
6. If

where, C is a constant of integration, then the function f (x) is equal to
(a) – 1/6x3
(b) – 1/2x3
(c) – 1/2x2
(d) 3/ x2
Answer
B
7. Which one of the following statements is not a tautology?
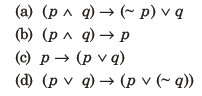
Answer
D
8.
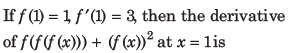
(a) 12
(b) 9
(c) 15
(d) 33
Answer
D
9. If three distinct numbers a, b and c are in GP and the equations

Answer
B
10. The minimum number of times one has to toss a fair coin so that the probability of observing at least one head is at least 90% is
(a) 2
(b) 3
(c) 5
(d) 4
Answer
D
11. Suppose that the points (h, k), (1, 2) and (-3, 4) lie on the line L1. If a line L2 passing through the points (k/h) and (4, 3) is perpendicular to L1, then k/h equals
(a) – 1/7
(b)1/3
(c) 3
(d) 0
Answer
C
12. Given that the slope of the tangent to


Answer
C
13. Let f : [-1, 3]→ R be defined as

where, [t]denotes the greatest integer less than or equal to t. Then, f is discontinuous at
(a) four or more points
(b) only two points
(c) only three points
(d) only one point
Answer
C
14. The height of a right circular cylinder of maximum volume inscribed in a sphere of radius 3 is
(a) √6
(b) 2√3
(c) √3
(d)2/3√3
Answer
B
15.
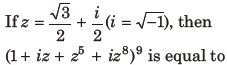
(a) 1
(b) (-1 + 2i )9
(c) -1
(d) 0
Answer
C
16. A student scores the following marks in five tests 45, 54, 41, 57, 43. His score is not known for the sixth test.
If the mean score is 48 in the six tests, then the standard deviation of the marks in six tests is
(a)10/3
(b)10/√3
(c)100/√3
(d)100/3
Answer
B
17. The number of integral values of m for which the equation
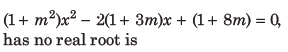
(a) 3
(b) infinitely many
(c) 1
(d) 2
Answer
B
18. In an ellipse, with centre at the origin, if the difference of the lengths of major axis and minor axis is 10 and one of the foci is at (0, 5√3), then the length of its latus rectum is
(a) 5
(b) 10
(c) 8
(d) 6
Answer
D
19.
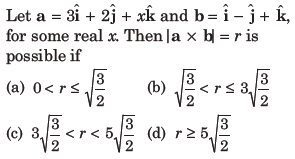
Answer
D
20.
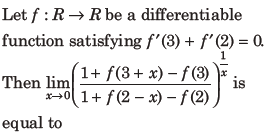
(a) e
(b) e-1
(c) e2
(d) 1
Answer
D
21. The vector equation of the plane through the line of intersection of the planes x + y + z = 1 and 2x + 3y + 4z = 5, which is perpendicular to the plane x – y + z = 0 is
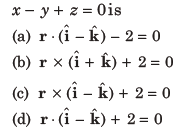
Answer
D
22. If the fourth term in the binomial
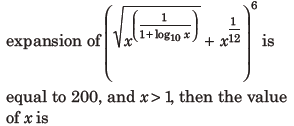
(a) 100
(b) 104
(c) 10
(d) 103
Answer
C
23. The tangent to the parabola y2= 4x at the point where it intersects the circle x2+y2=5 in the first quadrant, passes through the point
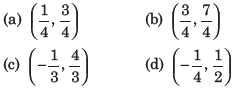
Answer
B
24. If the eccentricity of the standard hyperbola passing through the point (4, 6) is 2, then the equation of the tangent to the hyperbola at (4, 6) is
(a) 3x – 2y = 0
(b) x – 2y + 8 = 0
(c) 2x – y – 2 = 0
(d) 2x – 3y + 10 = 0
Answer
C
25.
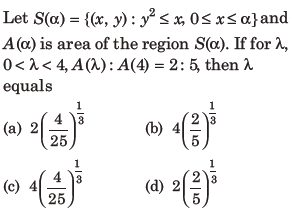
Answer
C
26. Let f (x) = ax (a > 0) be written as f (x) = f1 (x) + f2 (x) 1 2 , where f1 (x) is an even function and f2(x ) is an odd function. Then f1 (x+ y) +f1 (x-y) equals
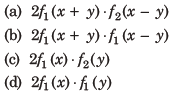
Answer
D
27. The number of four-digit numbers strictly greater than 4321 that can be formed using the digits 0, 1, 2, 3, 4, 5 (repetition of digits is allowed) is
(a) 306
(b) 310
(c) 360
(d) 288
Answer
B
28. Two vertical poles of heights, 20 m and 80 m stand apart on a horizontal plane. The height (in m) of the point of intersection of the lines joining the top of each pole to the foot of the other, from this horizontal plane is
(a) 15
(b) 16
(c) 12
(d) 18
Answer
B
29. If a point R(4, y, z) lies on the line segment joining the points P(2, – 3, 4) and Q(8, 0, 10), then the distance of R from the origin is
(a) 2 √21
(b) √53
(c) 2 √14
(d) 6
Answer
C
30. The tangent and the normal lines at the point ( √3, 1) to the circle x2+y2 =4 and the X-axis form a triangle. The area of this triangle (in square units) is
(a)1/3
(b)4/√3
(c)2/√3
(d)1/√3
Answer
C
