Sample Paper Class 12 Mathematics Set O
1. Slope of a line passing through P (2, 3) and intersecting the line, x + y = 7 at a distance of 4 units from P, is

Answer
C
2. If f (x) is a non-zero polynomial of degree four, having local extreme points at x = – 1, 0, 1, then the set S = {x ∈ R : f (x) = f (0)} contains exactly
(a) four rational numbers
(b) two irrational and two rational numbers
(c) four irrational numbers
(d) two irrational and one rational number
Answer
D
3. Four persons can hit a target correctly with probabilities 1/2,1/3,1/4 and 1/8 respectively. If all hit at the target independently, then the probability that the target would be hit, is
(a)1/192
(b)25/32
(c)7/32
(d)25/192
Answer
B
4.

(a) 2
(b) 4
(c) 3
(d) 16
Answer
C
5. If the line x – 1/2=y+1/3=z-2/4 meets the plane, x + 2y + 3z = 15 at a point P, then the distance of P from the origin is
(a) 7 / 2
(b) 9 / 2
(c) √5 / 2
(d) 2√5
Answer
B
6. If the line y = mx + 7 √3 is normal to the hyperbola x2/24-y2/18=1 then a value of m is
(a)3/5
(b)√152
(c)2/√5
(d)√5/2
Answer
C
7. If a tangent to the circle x2+y2=1 intersects the coordinate axes at distinct points P and Q, then the locus of the mid-point of PQ is
(a) x2 +y2-2x2y2=0
(b) x2+y2-2xy=0
(c) x2+y2-4x2y2=0
(d)x2+y2-16x2y2=0
Answer
C
8. If the function f : R- {1, – 1}→ A defined by f (x)= x2/1-x2 is surjective, then A is equal to
(a) R – {-1}
(b) [0, ∞)
(c) R – [-1, 0)
(d) R – (-1, 0)
Answer
C
9. The value of
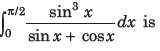
(a) π – 1/2
(b) π – 2/8
(c) π – 1/4
(d) π – 2/4
Answer
C
10. If one end of a focal chord of the parabola, y2 = 16 is at (1, 4), then the length of this focal chord is
(a) 22
(b) 25
(c) 24
(d) 20
Answer
B
11. The solution of the differential equation x dy/dx+2y=x2(x≠0) with y(1) = 1, is

Answer
A
12. All the points in the set

(a) circle whose radius is 2.
(b) straight line whose slope is -1.
(c) circle whose radius is 1.
(d) straight line whose slope is 1.
Answer
C
13. If the function f defined on (π/6, π/3) by

continuous, then k is equal to
(a)1/2
(b) 2
(c) 1
(d)1/√2
Answer
A
14. Let S = {θ ∈[-2π, 2π] : 2cos2 θ + 3sinθ = 0}, then the sum of the elements of S is
(a) 2π
(b) π
(c)5π/3
(d)13π/6
Answer
C
15. If the tangent to the curve, y = x3 + ax – b at the point (1, – 5) is perpendicular to the line,-x + y + 4 = 0, then which one of the following points lies on the curve ?
(a) (-2, 2)
(b) (2, – 2)
(c) (-2, 1)
(d) (2, – 1)
Answer
B
16. If the standard deviation of the numbers -1, 0, 1, k is 5 where k > 0,then k is equal to
(a)2√10/3
(b) 2 √6
(c) 4√5/3
(d) √6
Answer
B
17. Let p, q ∈R. If 2 – √3 is a root of the quadratic equation, x2+ px+ q = 0, then
(a) q2-4p-16=0
(b) p2-4q-12=0
(c) p2-4q+12=0
(d) q2+4p+14=0
Answer
B
18. A plane passing through the points (0, – 1, 0) and (0, 0, 1) and making an angle π/4 with the plane y – z + 5 = 0, also passes through the point
(a) ( √2, 1, 4)
(b) (- √2, 1, – 4)
(c) (- √2, – 1, – 4)
(d) ( √2, – 1, 4)
Answer
A
19 .

Answer
B
20. Let f (x) = 15 – lx – 10l ; x ∈R. Then,the set of all values of x, at which the function, g(x) = f (f (x)) is not differentiable, is
(a) {5, 10, 15, 20}
(b) {5, 10, 15}
(c) {10}
(d) {10, 15}
Answer
B
21. Let S be the set of all values of x for which the tangent to the curve y = f (x) = x3-x2-2x at(x,y) is parallel to the line segment joining the points (1, f (1)) and (-1, f (-1)), then S is equal to
(a){1/3,-1}
(b){1/3,1}
(c) {-1/3,1}
(d) {-1/3,-1}
Answer
C
22. For any two statements p and q, the negation of the expression

Answer
A
23. If the fourth term in the binomial

(a) 8 -2
(b) 83
(c) 8
(d) 82
Answer
D
24. The value of

Answer
D
25. Let α and β be the roots of the equation x2 +x+1 = 0. Then, for y≠ 0 in R,

(a) y(y2 – 1)
(b) y (y2 – 3)
(c) y3 – 1
(d) y3
Answer
D
26. The area (in sq units) of the region
A = {(x, y) : x2 ≤ y ≤ x+2}
(a)13/6
(b)9/2
(c)31/6
(d)10/3
Answer
B
27. The integral
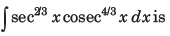
equal to (here C is a constant of integration)

Answer
B
28. A committee of 11 members is to be formed from 8 males and 5 females. If m is the number of ways the committee is formed with at least 6 males and n is the number of ways the committee is formed with at least 3 females, then
(a) m = n = 68
(b) m + n = 68
(c) m = n = 78
(d) n = m – 8
Answer
C
29. Let the sum of the first n terms of a non-constant AP a1,a2,a3…. be 50n+n(n-7/2 A, where A is a constant. If d is the common difference of this AP, then the ordered pair (d, a50 ) is equal to
(a) (A, 50 + 46A)
(b) (50, 50 + 45A)
(c) (50, 50 + 46A)
(d) (A, 50 + 45A)
Answer
A
30.

Answer
B
