SECTION-A

In this section, attempt any 16 questions out of Questions 1 –20.
Each Question is of 1 mark weightage.

1. What is the principal value of tan–1(1) ?
(A) π/8
(B) π/6
(C) π/3
(D) π/4

2. Which of the function is decreasing in the interval (π/2 ,π) ?
(A) sin x
(B) e^x
(C) log x
(D) none of these

3. The inverse of the matrices

4. Consider matrix A =

(A) column matrix
(B) Row matrix
(C) scalar matrix
(D) Null matrix

5. The function f(x) = 4-X²/4x – x³
(A) discontinuous at only one point
(B) discontinuous at exactly two points
(C) discontinuous at exactly three points
(D) none of these

6. Given that a matrix A =

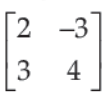
satisfies the equation x² – 6x + 17 = 0. Then the inverse of the matrix by using the equation is:
(A) -1/17(A – 6I2)
(B) 1/17 (A – 6I2)
(C) 1/17 (A + 6I2)
(D) -1/17 (A + 6I2)

7. The relation R is defined on the set of natural numbers as {(a, b): 2a = b}. which of the following can be an element of the given relation?
(A) (2, 1), (4, 2), (6, 3)
(B) (1, 2), (2, 4), (3, 6)
(C) All of the above
(D) None of these

8. Given the equations x – 2y – 4 = 0 and –3x + 5y + 7 = 0 are consistent and has the solution as
(A) x = –6, y = –5
(B) x = 6, y = 5
(C) x = –6, y = 5
(D) x = 6, y = –5

9. Find slope of the normal to the curve y = 5x³ at x = 1/3 ?
(A) -3/5
(B) -2/5
(C) -6/5
(D) -9/5

10. What is the principal value of cosec–1(2)?
(A) π/8
(B) π/6
(C) π/3
(D) π/12

11. If f(x₁) = f(x₂) ⇒ x₁ = x₂ ∀ x₁.x₂ ∈ A then the function f : A → B is
(A) one-one
(B) one-one onto
(C) onto
(D) many one

12. If y = asec²q and x = acosec²q then (dy/dx)_{θ = π/4} will be
(A) 0
(B) –1
(C) 2
(D) 4

13. If A₂ – A + I = 0 then the inverse of A is
(A) A – I
(B) I – A
(C) A + I
(D) A

14. If y = 5t³/tan t then dy/dt will be

15. The determinant of matrix A =

is given as |A| = –37, then calculate the determinant of

(A) –37
(B) –74
(C) 74
(D) –296

16. If y = 2x – log x then the slope of tangent at x = 1 is
(A) 2
(B) 3
(C) –2
(D) 1

17. If matrix A is inverse of matrix B, then (AB) will be equal to:
(A) A + B
(B) (BA)
(C) B/A
(D) A – B

18. If y = cos²θ/sin² θ – cos²θ then dy/dx will be
(A) y = 2 cos θ/sin θ – cos² θ
(B) y = sin θ/sin² θ – tan θ
(C) 0
(D) y = cos tan θ/sin² θ – cos²θ

19. Minimize Z = 14x – 15y subject to the constraints: x + y ≤ 7, 3x + 2y – 6 ≥ 0, x ≥ 0, y ≥ 0
(A) (0, 3)
(B) (3, 2)
(C) (0, 7)
(D) (3, 4)

20. In the interval (0,π/2) local maximum of the function f (x) = 2sinx – x + 1 is at
(A) x = π/32
(B) x = π/4
(C) x = π/12
(D) x = π/3

SECTION-B

In this section, attempt any 16 questions out of the Questions 21 -40.
Each Question is of 1 mark weightage.

21. Given a function, f(x) = x³ + x then the function is
(A) Bijective
(B) Injective
(C) Surjective
(D) None of these

22. If xy5 + 2y + 5x = 0 then dy/dx = y1 will be

23. Neha goes to the market with Rs 500 to buy salt which is available in packets of 1kg. The price of one packet of salt is ₹30. If y denotes the number of the packets of salts which she buys, then the constraints are_______ and________
(A) y ≥ 0 and 30y > 500
(B) y ≤ 0 and y < 500
(C) y > 0 and 30y ≤ 500
(D) y ≥ 0 and 30y ≤ 500

24. If y = 1/√x² + y then dy/dx will be
(A) xy³/2 – y³
(B) y³x/2+y³
(C) -2y³x/2+y³
(D) 2y³x/2+y³

25. Let AX = B be a system of n-linear equations in n unknowns and |A| = 0 and (adj A)B ≠ 0, then the system of linear equations is
(A) Consistent
(B) Inconsistent
(C) Can’t determined
(D) None of these

26. Angle between two curves y = x² – 5, y = x⁴ at x = 1 ?
(A) 2/9
(B) 2/6
(C) 4/3
(D) 2/3

27. The principal value of sin-1 (-1/2) + sin -1 (1/2) is
(A) π/3
(B) -π/6
(C) π/6
(D) 0

28. The area of a triangle with vertices (–3, 0), (3, 0) and (0, k) is 9 sq. units. Then, the value of k will be
(A) 9
(B) 3
(C) –9
(D) 6

29. The smallest value of the polynomial x³ – 18x² + 96x in [0, 9] is
(A) 126
(B) 0
(C) 135
(D) 160

30. Let R be the set of real numbers then A = {(x, y) ∈ R × R : y – x is an integer} is a
(A) only reflexive
(B) only symmetric
(C) transitive relation
(D) empty relation

31. The function f(x) = cot x is discontinuous on the set
(A) {x = np; n∈Z}
(B) {x = 2np; n∈Z}
(C) {x = (2n+1)π/2 ; n∈Z}
(D) {x =nπ/2 ; n∈Z}

32. Given a matrix A =

(A) 0
(B) 5
(C) 3
(D) 1

33. Which of the following term is not a part of a linear programming problem?
(A) Concave region
(B) Slack variables
(C) Objective function
(D) Feasible solution

34. Consider the function y = f(x) defined over [a, b], function has absolute maximum at b and local maximum at c where
(A) c ≠ a, c ≠ b
(B) c = a, c ≠ b
(C) c ≠ a, c = b
(D) c = a = b

35. Assume X, Y, Z, W and P are matrices of order 2 × n, 3 × k, 2 × p, n × 3 and p × k, respectively. If n = p, then the order of the matrix 7X – 5Z is:
(A) p × 2
(B) 2 × n
(C) n × 3
(D) p × n

36. If sin(sin–1x) = x, then
(A) –p/2 < x < p/2
(B) –1 ≤ x ≤ 1
(C) –1 < x < 1
(D) –p/2 ≤ x ≤ p/2

37. Consider the non-empty set consisting of children in a family and a relation R defined as aRb if a is brother of b. Then R is
(A) symmetric but not transitive
(B) transitive but not symmetric
(C) neither symmetric nor transitive
(D) both symmetric and transitive

38. If A and B are invertible matrices, then which of the following is not correct?
(A) adj A = A .A^-1
(B) det(A- ) = [det(A)] ^-1 
(C) (AB) ^-1 = B ^-1 A ^-1 
(D) (A + B)^-1 = B^-1 + A^-1

39. Let R be the relation in the set {1, 2, 3, 4} given by R = {(1, 2), (2, 2), (1, 1), (4, 4), (1, 3), (3, 3), (3, 2)}.
Choose the correct answer.
(A) R is reflexive and symmetric but not transitive
(B) R is reflexive and transitive but not symmetric
(C) R is symmetric and transitive but not reflexive
(D) R is an equivalence relation.

40. If A =

and A + A’ = I, then the value of α is:
(A) π/6
(B) π/3
(C) π
(D) 3π/2

SECTION-C

In this section, attempt any 8 questions. Each question is of 1-Questions 46-50 are based on a Case-Study.

41. Non-negative restriction of decision variables satisfy_________
(A) Feasible solution
(B) Infeasible solution
(C) Graphical solution
(D) All of the above

42. If y = 3cos²x + 4sin²x then,
(A) d²y/dx² + 4 = 0
(B) d²y/dx – 3y = 0
(C) d²y/dx² – 4y = 0
(D) d²y/dx² + 2y = 0

43. The equation of normal to the curve 3x² – y² = 8 which is parallel to the line x + 3y = 8 is
(A) 3x – y = 8
(B) 3x + y + 8 = 0
(C) x + 3y ± 8 = 0
(D) x + 3y = 0

44. The feasible region for a LPP is shown in fig.

The minimum value of z = 3x + 3 – 5y is
(A) –595
(B) 550
(C) 0
(D) 470

45. If

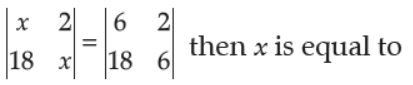
(A) 6
(B) ±6
(C) –6
(D) 0

CASE-STUDY

P(x) = –5x² + 125x + 37500 is the total profit function of a company, where x is the production of the company.

Based on the given information, answer the following questions.

46. What will be the production when the profit is maximum?
(A) 37,500
(B) 12.5
(C) – 12.5
(D) – 37,500

47. What will be the maximum profit?
(A) ₹ 38,28,125
(B) ₹ 38,281.25
(C) ₹ 39,000
(D) None of these

48. Check in which interval the profit is strictly increasing .
(A) (12.5, ∞)
(B) for all real numbers
(C) for all positive real numbers
(D) (0, 12.5)

49. When the production is 2 units, what will be the profit of the company?
(A) 37,500
(B) 37,730
(C) 37,770
(D) None of these

50. What will be production of the company when the profit is ₹ 38,250?
(A) 15
(B) 30
(C) 10
(D) data is not sufficient to find