Sample Paper Class 12 Mathematics Set H
SECTION – A
1. If A is a square matrix satisfying A’A = I , write the value of |A| .
Sol. A’A = I ⇒ |A’A| = |I|
⇒ |A’||A| =1 ⇒ |A|2 =1
∴ A = ±1.
2. If y = x|x|, find dy/dx for x < 0
Sol. y = x|x| = x(−x) = −x2 [∵ x < 0
∴ dy/dx = −2x.
3. Find the order and degree (if defined) of the differential equation
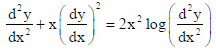
Sol. Order : 2, Degree : Not defined.
4. Find the direction cosines of a line which makes equal angles with the coordinate axes.
Sol. Since the line is making equal angles with the coordinate axes so, α = β = γ .
So, cos2 α + cos2 β + cos2 γ =1
⇒ cos2 α + cos2 α + cos2 α = 1
⇒ cos2 α = 1/3 ⇒ cosα = ±1/√3
Hence the d.c.’s of the line are ±1/√3 , ±1/√3 ,±1/√3
OR
A line passes through the point with position vector 2î − ĵ+ 4 k̂ and is in the direction of
the vector î + ĵ− 2 k̂ . Find the equation of the line in Cartesian form.
Sol. The line passes through (2, –1, 4) and its direction cosines are 1, 1, –2.

SECTION – B
5. Examine whether the operation * defined on R, the set of all real numbers, by a * b = √a2 + b2 is a binary operation or not, and if it is a binary operation, find whether it is associative or not.
Sol.

6.
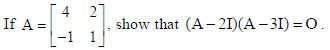
Sol.
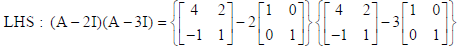

7. Find :
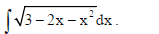
Sol.
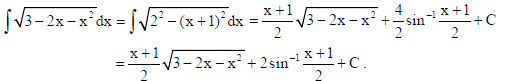
8. Find :
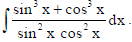
Sol.
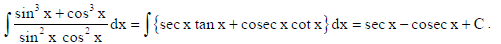
OR
Find :
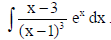
Sol.

9. Find the differential equation of the family of curves y = Ae2x + Be−2x , where A and B are arbitrary constants.
Sol. y = Ae2x + Be−2x…(i)

10. If |a̅| = 2, |b̅| = 7 and a̅ × b̅ = 3î + 2ĵ+ 6 k̂, find the angle between a̅ and b̅.
Sol.

OR
Find the volume of a cuboid whose edges are given by −3î + 7ĵ+ 5 k̂ , −5î + 7ĵ−3 k̂ and
7î −5ĵ−3 k̂ .
Sol.
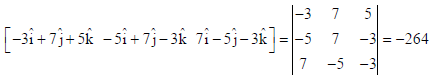
Hence volume of the cuboid = 264 units3 .
11. If P(not A) = 0.7, P(B) = 0.7 and P(B|A) = 0.5 , then find P(A|B).
Sol. P(A∩B) = P(A) × P(B| A) = {1− P(not A)} × 0.5 = 0.3×0.5 = 0.15.
So, P(A | B) = P(A∩B) / P(B) = 0.15/0.7 = 15/70 or, 3/14.
12. A coin is tossed 5 times. What is the probability of getting (i) 3 heads, (ii) at most 3 heads?
Sol.

OR
Find the probability distribution of X, the number of heads in a simultaneous toss of two coins.
Sol. Let X : no. of heads ∴X = 0,1, 2.
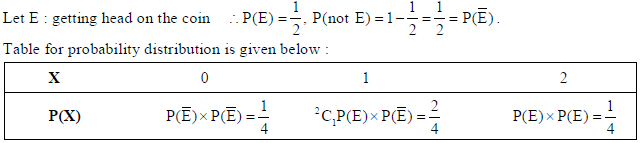
SECTION – C
13. Check whether the relation R defined on the set A = {1, 2, 3, 4, 5, 6} as R = {(a, b) : b = a +1} is reflexive, symmetric or transitive.
Sol. Here R = {(1, 2),(2,3),(3,4),(4,5), (5,6)}.
As (1,1) ∉ R for 1 ∈ A , so R isn’t reflexive.
Also (1,2) ∈ R but (2,1) ∉ R for 1, 2 ∈ A , so R isn’t symmetric.
Similarly, (1,2) ∈ R, (2,3) ∈ R but (1,3) ∉ R for 1, 2,3 ∈ A , so R isn’t transitive.
OR
Let f : N→Y be a function as f (x) = 4x + 3,
where Y ={y ∈ N: y = 4x + 3, for some x ∈ N}. Show that f is invertible. Find its inverse.
Sol. We’ve f : N→Y , f (x) = 4x + 3.
Let x1 , x2 ∈ N such that f (x1) = f (x2) .
∴ 4x1 + 3 = 4x2 + 3 ⇒ x1 = x2.
So, f is one-one.
Let y = f (x) = 4x + 3.
Note that for all x ∈ N, 4x + 3 ∈ N i.e., y ∈ N.
That is, codomain of f = range of f = Y.
Hence, f is onto.
Therefore, f is bijective and it’s invertible.
Now y = 4x+3 ⇒ x = y−3/4
∴ f −1 :Y→N is given as f −1(y) = y−3/4 or, f −1(x) = x−3/4.
14.
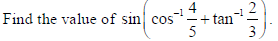
Sol.
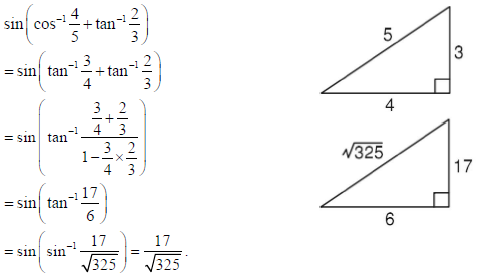
15. Using properties of determinants, show that
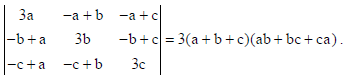
Sol.

Expanding along C1 ,
⇒ Δ = (a + b + c){(a + 2b)(a + 2c) − (a − b)(a − c)}
⇒ Δ = (a + b + c){a2 + 2ca + 2ab + 4bc − a2 + ac + ab − bc}
⇒ Δ = (a + b + c){3ab + 3bc + 3ca}
∴ Δ = 3(a + b + c)(ab + bc + ca) =RHS.
16.
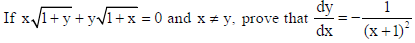
Sol.
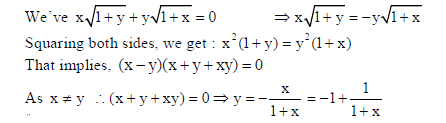

OR
If (cos x)y = (sin y)x , find dy/dx.
Sol. We have (cos x)y = (sin y)x
⇒ log(cos x)y = log(sin y)x
⇒ ylog(cos x) = x log(sin y)
On differentiating w. r. t. x both sides, we get :
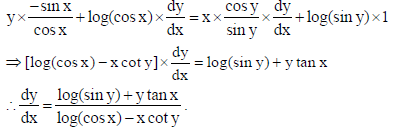
17. If (x − a)2 + (y − b)2 = c2 , for some c > 0 , prove that

is a constant independent of a and b.
Sol. We have (x − a)2 + (y − b)2 = c2…(i)

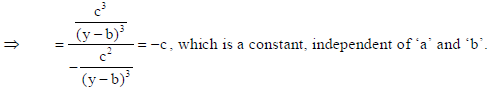
18. Find the equation of the normal to the curve x2 = 4y which passes through the point (–1, 4).
Sol. Let (α,β) be the point of contact on the curve x2 = 4y so, α2 = 4β…(i)

19. Find :

Sol.
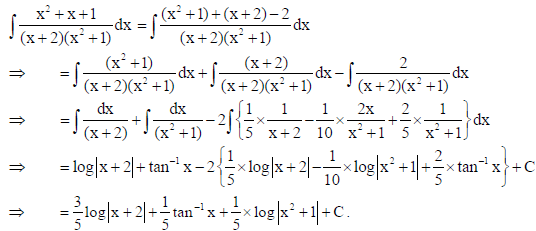
20. Prove that
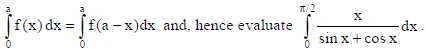
Sol.

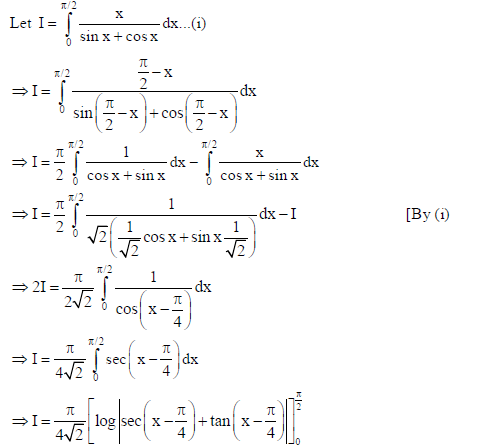
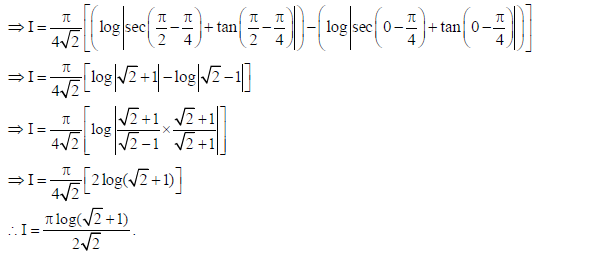
21. Solve the differential equation :

Sol.
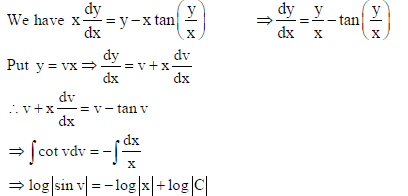

OR
Solve the differential equation :

Sol.

22. The scalar product of the vector a̅ = î + ĵ+ k̂ with a unit vector along the sum of vectors b̅ = 2î + 4ĵ− 5 k̂ and c̅ = λî + 2ĵ+ 3 k̂ is equal to 1. Find the value of λ and hence find the unit vector along b̅ + c̅.
Sol.
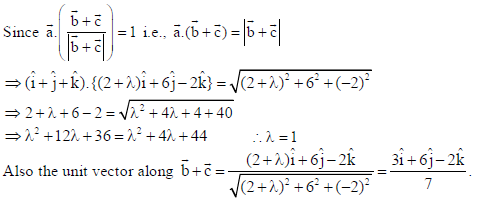
23.

are perpendicular, find the value of λ .
Hence find whether the lines are intersecting or not.
Sol. The d.r.’s of the given perpendicular lines are respectively −3,2λ,2; 3λ,2,−5
So, (−3)(3λ) + (2λ)(2) + (2)(−5) = 0 ⇒λ = −2 .
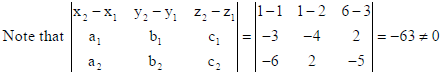
Therefore, the lines are not intersecting (as for intersecting lines, S.D. = 0 ).
SECTION – D
24.

Hence solve the system of equations : x + 3y + 4z = 8 , 2x + y + 2z = 5 and 5x + y + z = 7 .
Sol.
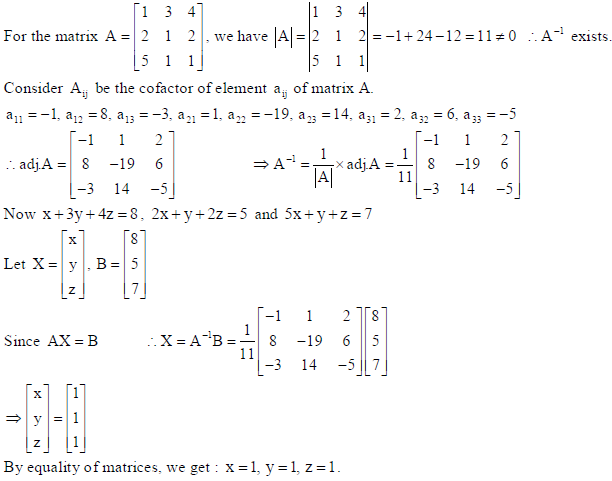
OR
Find the inverse of the following matrix, using elementary transformations :
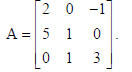
Sol. As we know that A = IA


25. Show that the height of the cylinder of maximum volume that can be inscribed in a sphere of radius R is 2R/√3 . Also find the maximum volume.
Sol. Let r and h be the radius and height of cylinder inscribed in a sphere of radius R.


26. Using method of integration, find the area of the triangle whose vertices are (1, 0), (2, 2) and (3,1).
Sol.
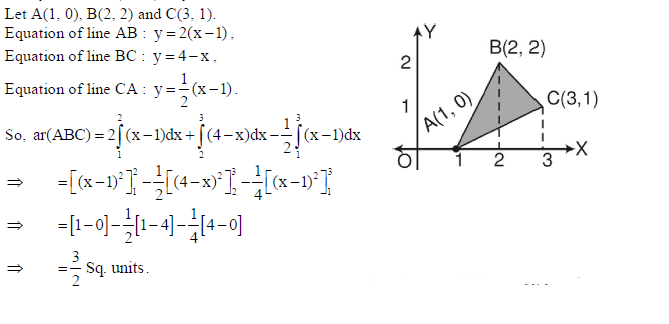
OR
Using method of integration, find the area of the region enclosed between two circles
x2 + y2 = 4 and (x − 2)2 + y2 = 4 .
Sol.

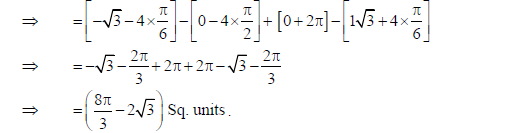
27. Find the vector and Cartesian equations of the plane passing through the points having position vectors î + ĵ− 2 k̂ , 2î − ĵ+ k̂ and î + 2ĵ+ k̂ . Write the equation of a plane passing through a point (2, 3, 7) and parallel to the plane obtained above. Hence, find the distance between the two parallel planes.
Sol. The coordinates of the points on the required plane is (1, 1, –2), (2, –1, 1) and (1, 2, 1).
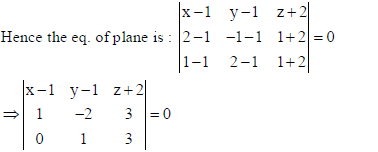
⇒ −9(x −1) −1(3y −3− z − 2) = 0⇒ 9x + 3y − z −14 = 0, which is the Cartesian eq. of plane.
Also the vector eq. is r̅.(9î + 3ĵ− k̂ ) −14 = 0…(i)
Also the eq. of plane through (2, 3, 7) and parallel to the plane (i) is :
9(x − 2) + 3(y −3) − (z − 7) = 0 i.e., 9x + 3y − z − 20 = 0…(ii)

OR
Find the equation of the line passing through (2, –1, 2) and (5, 3, 4) and of the plane passing through (2, 0, 3), (1, 1, 5) and (3, 2, 4). Also, find their point of intersection.
Sol. The equation of the line passing through (2, –1, 2) and (5, 3, 4) is :
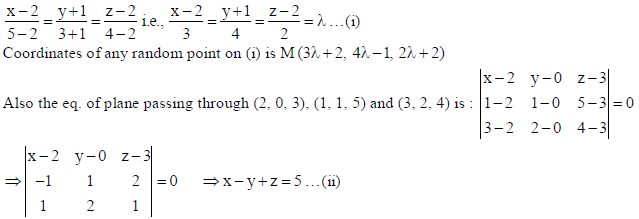
If (i) and (ii) intersect then, point M must satisfy (ii), i.e., 3λ + 2 − 4λ +1+ 2λ + 2 = 5 ⇒ λ = 0
Therefore, M(2, −1, 2) .
28. There are three coins. One is a two-headed coin, another is a biased coin that comes up heads 75% of the time and the third is an unbiased coin. One of the three coins is chosen at random and tossed. If it shows heads, what is the probability that it is the two-headed coin?
Sol. Let E1 , E2 , E be the events that two-headed coin, biased coin and unbiased coin is chosen,
respectively. Also, let E : the coin tossed shows head.

29. A company produces two types of goods, A and B, that require gold and silver. Each unit of type A requires 3 g of silver and 1 g of gold while that of type B requires 1 g of silver and 2 g of gold. The company can use at the most 9 g of silver and 8 g of gold. If each unit of type A brings a profit of `40 and that of type B `50, find the number of units of each type that the company should produce to maximize profit. Formulate the above LPP and solve it graphically and also find the maximum profit.
Sol. Let the company produces x no. of units of goods A.
Let the company produces y no. of units of goods B.

