Part–A
Section – I

All questions are compulsory. In case of internal choices attempt any one.

Q1. Check whether the function f : R → R given by f (x) = sin x ” x ∈ R is one-one or not. 
Answer : f (x) is not one-one

OR

Let R be a relation on the set of natural number N as follows.
R = {(x, y) : x ∈ N, y ∈ N and 2x + y = 24}
Find the domain of R.
Answer : Domain of R : {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11}

Q2. Show that each of the relation R in the set A = {x ∈ Z : 0 ≤ x ≤ 12}, given by
R = {(a, b) : a = b} is an equivalence relation. 
Answer : 

Q3. Show that the function f (x) = x³ + 5x + 1 for real x is one-one and onto.
Answer : f is one-one and onto R

OR

Let A = {1, 2, 3, 4}; Define a relation which is reflexive, trans𝑖̂ive but not symmetric.
Answer : {(1, 1), (2, 2), (3, 3), (4, 4), (1, 3), (3, 4), (1, 4)}.

Q4. Construct a 3 × 3 matrix whose elements are given by a_ij = 2i – 3j.
Answer : 

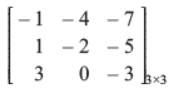
Q5. If

Answer : 

OR

If possible, find the sum of A and B where

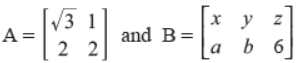
Answer : Not possible.

Q6. Compute: 

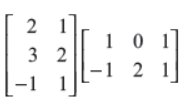
Answer : 

Q7. Find: ∫ cos(4 − 3x)+ sin (4 − 3x)] dx.
Answer : −1/3 sin (4 – 3x) + 1/3 cos (4 – 3x) + C

OR

Evaluate: 

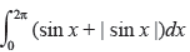
Answer : 4

Q8. Find the area under the graph of y = x over the interval [1, 5].
Answer : 12 sq. units

Q9. Wr𝑖̂e the order and degree of the differential equation (dy/dx)4 + 3y d²y/dx² = 0.
Answer : Order = 2, Degree = 1

OR

Solve: dy/dx = e^x+y.
Answer : e^x + e^–y + C = 0

Q10. Show that [𝑖̂ – 𝑗̂, 𝑗̂ – 𝑘̂, 𝑘̂ – 𝑖̂] = 0.
Answer : …….?

Q11. Evaluate 𝑖̂ · (𝑗̂ × 𝑘̂) + (𝑖̂ × 𝑘̂) · 𝑗̂ .
Answer : 0

Q12. If (𝑖̂ 𝑗̂ 𝑘̂) is an orthonormal system of vectors and 𝑖̂, 𝑖̂ + 𝑗̂, 𝑖̂ + 𝑗̂ + 𝑘̂ are adjacent sides of parallelopiped, find 𝑖̂s volume.
Answer : 1 cu. unit

Q13. Determine whether the following pair of lines intersect 
x–1/2 = y+1/3 = z;  x+1/5 = y–2/1 = z–2/0.
Answer : Given pair of lines do not intersect.

Q14. Find the equation of the straight line through (1, – 2, 3) and equally inclined to the axes. 
Answer : x – 1 = y + 2 = z – 3

Q15. Two dice are thrown, find the probability that the numbers appeared have a sum 8 if it is known that the second dice always exhibits 4. 
Answer : 1/6

Q16. If A and B are independent events such that P(A ∪ B) = 0.6 and P(A) = 0.2, find P(B).
Answer : 0.5

Section-II
Both the Case study-based questions are compulsory. Attempt any 4 sub-parts from each question (17–18). Each sub-part carries 1 mark.

Q17. Child labour is work which harms children and prevents them from attending the school. It also threatens children’s physical, mental or emotional well being. It violates the child freedom and human rights. We should discourage child labour.
In a competition, some braves children try to inflate some huge spherical balloons bearing slogans against the child labour. 

Based on the above information, answer the following questions.
(i) Rakesh is inflating a balloon at the rate of 900 cubic centimetres of gas per second. If the radius of the balloon is 15 cm, the increasing rate of radius of balloon is 
(a) 7/22 cm/sec
(b) 9/22 c//sec
(c) 1/2 cm/sec
(d) None of theseAnswer : A

(ii) The radius of a balloon is increasing at the rate of 10 cm/sec. At what rate is the surface of the balloon increasing when radius is 15 cm? 
(a) 1232 p cm2/sec
(b) 1200 p cm2/sec
(c) 835 p cm2/sec
(d) 725 p cm2/secAnswer : B

(iii) The surface area of a spherical bubble is increasing at the rate of 2 cm2/sec. The rate at which the volume of the bubble is increasing, at the instant its radius is 6 cm, will be 
(a) 8 cm3/sec
(b) 5 cm3/sec
(c) 6 cm3/sec
(d) 7 cm3/secAnswer : C

(iv) A balloon is tied with a string of 28 m. Anil wants to cut it in two pieces. He wants to form a square using one piece and a circle using another one. From where should the
string to be cut so that combined area is minimum? 
(a) 15.5 m
(b) 12.32 m
(c) 24.6 m
(d) 16.4 mAnswer : B

(v) If the radius of a spherical balloon is measured as 25 cm with an error of 0.02 cm, then the approximate error in calculating its volume is 
(a) 162.44 cm3
(b) 192 cm3
(c) 157.14 cm3
(d) None of these.Answer : C

Q18. An Intelligence quotient (IQ) is a total score derived from a set of standardized tests or subtests designed to assess human intelligence.

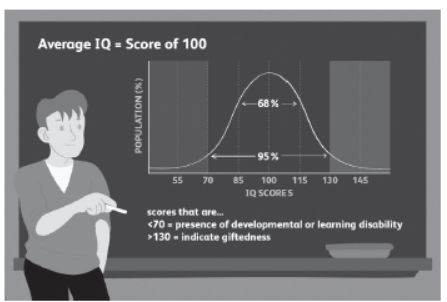
Using Raven’s Progressive Matrices (RPM), IQ of students of classes 10th to 12th of a school is measured. The results are as follows:
• In class 10, having 60% boys, 5% of the boys and 10% of the girls have an IQ of more than 150.
• In class 11, having 48% girls, 12% of the girls and 18% of the boys have an IQ of less than 150.
• In class 12, having 40% boys, 15% of the boys and 20% of girls have an IQ of more than 100. A student is selected at random from a class.
Based on the above information answer the following:

(i) It is found that the IQ of selected student from class 10 is more than 150. The probability that the selected student is a boy will be: 
(a) 3/7
(b) 5/9
(c) 4/13
(d) 2/9Answer : A

(ii) It is found that the IQ of selected student from class 11 is more than 150. The probability that the selected student is a girl will be: 
(a) 532 /1061
(b) 528/1061
(c) 525/1061
(d) 567/1061Answer : B

(iii) It is found that the IQ of selected student from class 12 is more than 100. The probability that the selected student is a boy will be: 
(a) 2/3
(b) 1/3
(c) 4/3
(d) 5/3Answer : B

(iv) A girl is selected, who have an IQ of less than 150, then the probability that she belongs to class 10 will be: 
(a) 3/5
(b) 7/17
(c) 17/7
(d) 12/31Answer : D

(v) A student is selected, who have an IQ of less than150, then probability that student is a boy of class 11 will be: 
(a) 17/21
(b) 7/22
(c) 13/21
(d) 5/12Answer : C

Part–B
Section–III
All questions are compulsory. In case of internal choices attempt any one.

Q19. Write the principal value of tan^–1 (–1)
Answer : –π/4

Q20. If

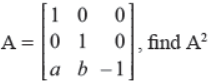
Answer : 

OR

If

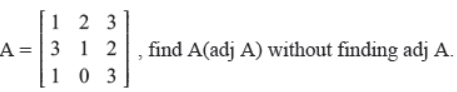
Answer : 

Q21. If

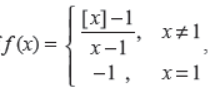
then show whether f (x) is continuous at x = 1. 
Answer : f (x) is not continuous at x = 1.

Q22. Find the equation of the tangent to the parabola y2 = 4ax at (at², 2at).
Answer : ty = x + at²

Q23. Evaluate:  

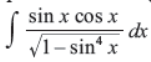
Answer : 1/2 sin^–1 (sin²x) + C

OR

Evaluate: 

Answer : π/2

Q24. Find the area of the region bounded by the curves y2 = 4x, y-axis and the line y = 3.
Answer : 9/4 sq. units

Q25. Solve the differential equation dy/dx = 1 + y²/ 1+x² .
Answer : y – x = C(1 + xy)

Q26. Find the number of distinct real values of λ, for which the vectors
– λ² 𝑖̂ + 𝑗̂ + 𝑘̂, 𝑖̂ – λ²𝑗̂ + 𝑘̂ and 𝑖̂ + 𝑗̂ – λ²𝑘̂ are coplanar.
Answer : λ = ± √2

Q27. Find the vector equation of the line through the point A(–1, 2, 3) and parallel to the line
x+2/2 = 2y–7/6 = 5–z/6 .
Answer : x+1/2 = y–2/2 = z–3/6

Q28. Let A and B be two independent events such that P(A) = 0.4, P(B) = p and P(A ∪ B) = 0.7. 
Find the value of p for which A and B are independent.
Answer : p = 1/2

OR

A die is tossed thrice. Find the probability of getting an odd number at least once.
Answer : 7/8

Section-IV
All questions are compulsory. In case of internal choices attempt any one.

Q29. Consider the set N × N, the set of all ordered pairs of natural numbers.
Let R be the relation in N × N which is defined by (a, b) R (c, d) if and only if ad = bc. Prove that R is an equivalence relation. 
Answer : ad=bc in an equivalence relation.
Symmetric:
if (a,b)R(c,d)∈N×N
⇒ad=bc
⇒bc=ad
⇒(c,d)R(a,b)
R is symmetric
Reflexive:
If (a,b)∈N×N
⇒ab=ab
(a,b)∈(a,b) . So R is reflexive.
Transitive:
If (a,b)R(c,d) and(c,d)R(e,f)
⇒ad=bc and cf=de
⇒ a/b = c/d and c/d = e/f
⇒ a/b = e/f
af=eb
(a,b)R(e,f)∈N×N
So R is transitive
Therefore R is in equivalence relation.

Q30. Differentiate tan x + tan x + tan x w.r.t x. 
Answer :

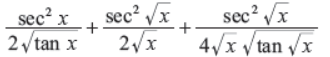
Q31. Discuss the continuity of the sine function. 
Answer : f (x) is continuous at each point belongs to R

OR

If x = 2/t² y = t³ – 1, then find d²y/dx².
Answer : 15/16 t⁷

Q32. Find the intervals in which the function is strictly increasing or decreasing x² + 2x – 5.
Answer : f (x) is decreasing for x < – 1 and f (x) is strictly increasing for x > – 1.

Q33. Evaluate: ∫ dx/x(x⁴– 1).
Answer : 

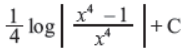
Q34. Using integration, find the area of the triangular region whose sides have the equations y = 2x + 1, y = 3x +1 and x = 4.
Answer : 8 sq. units

OR

The area between x = y2 and x = 4 is divided into two equal parts by the line x = a. Find the value of a.
Answer : a = 4^2/3

Q35. Find the general solution for differential equation x⁵ dy/dx = –y⁵.
Answer : x^–4 + y^–4 = C

Section-V

All questions are compulsory. In case of internal choices attempt any one.

Q36. If

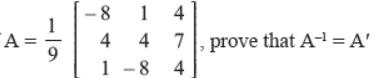
Answer : …..?

OR

For the matrix

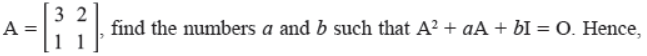
Answer :

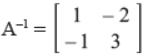
Q37. Find the equation of the plane passing through the line of intersection of the planes ( Image )
Answer : y – 3z + 6 = 0

OR

Find the equation of the plane passing through the line of intersection of the planes
2x + y – z = 3 and 5x – 3y + 4z + 9 = 0 and parallel to the line 
x–1/2 = y–3/4 = z–5/5.
Answer : 7x + 9y – 10z – 27 = 0

Q38. Solve the following linear programming problem (L.P.P.) graphically. 
Minimise Z = 60x + 80y subject to constraints;
3x + 4y ≥ 8
5x + 2y ≥ 11
x ≥ 0, y ≥ 0
Answer : Smallest value of Z is 160. The feasible region is unbounded.

OR

The corner points of the feasible region determined by the system of linear constraints are as shown below:   

Let Z = px + qy where p, q > 0. Find the condition on p and q so that the maximum of Z occurs at both (3, 4) and (0, 5).
Answer : q = 3p