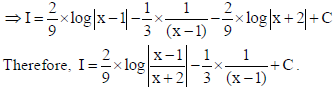Sample Paper Class 12 Mathematics Set G
SECTION – A
Question number 1 to 20 carry 1 mark each.
1. If a̅ = î + λĵ+ k̂ and b̅ = î + ĵ+ k̂ and |a̅ + b̅| = |a̅| + |b̅|, then the value of λ is
(a) 1
(b) –1
(c) 2
(d) – 2
Answer
A
2. The order and the degree of the differential equation
(dy/dx)3 + (d3y/dx3)3 + 5x = 0 are
(a) 3; 6
(b) 3; 3
(c) 3; 9
(d) 6; 3
Answer
B
3. If sec−1(1+x/1 – y) = a, then dy/dx is equal to
(a) x –1/y –1
(b) x –1/y +1
(c) y –1/x +1
(d) y +1/x −1
Answer
C
4.

Answer
A
5.

(a) 0
(b) –1
(c) 1
(d) 2
Answer
A
6. ∫ex/x+1 [1 (x + 1) log (x + 1)]dx equals
(a) ex/x+1 + c
(b) ex x/x+1 + c
(c) ex log(x +1) + ex + c
(d) ex log(x +1) + c
Answer
D
7.
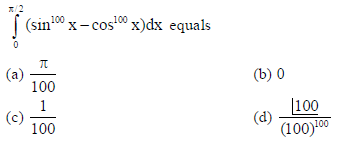
Answer
B
8. The probability of solving a specific question independently by A and B are 1/3 and 1/5 respectively. If both try to solve the question independently, the probability that the question is
solved, is
(a) 7/15
(b) 8/15
(c) 2/15
(d) 14/15
Answer
A
9. The objective function of an LPP is
(a) a constant
(b) a linear function to be optimized
(c) an inequality
(d) a quadratic expression
Answer
B
10. If the two lines
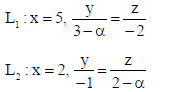
are perpendicular, then the value of α is
(a) 2/3
(b) 3
(c) 4
(d) 7/3
Answer
D
Fill in the blanks
11. The integrating factor of the differential equation x dy/dx – y = log x is _________.
Sol.

12. Two angles of a triangle are cot−1 2 and cot−1 3 . The third angle of the triangle is _________.
Sol. Let the third angle of the triangle be x then, cot−1 2 + cot−1 3+ x = π
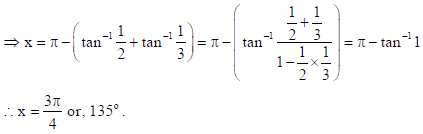
13. From a pack of 52 cards, 3 cards are drawn at random (without replacement). The probability that they are two red cards and one black card, is _________.
Sol.

14. A square matrix A is said to be singular if _________.
Sol. Det.(A) = 0.
OR

Sol.
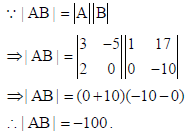
15. If x = et sin t, y = et cos t , then the value of dy/dx at t = π/4 is _________.
Sol. Here x = et sin t, y = et cos t

Question number 16 to 20 are very short answer type questions.
16. If f (x) = 1– x/1+ x, then find (fof )(x) .
Sol.

17.
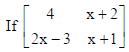
is symmetric matrix, then find the value of x.
Sol. For a symmetric matrix A, we have aij = aji.

That is, x + 2 = 2x −3
∴ x = 5.
OR
If A is a square matrix such that A2 = A, then find (2 + A)3 –19A .
Sol. (2 + A)3 –19A
On rewriting this, we get : (2I +A)3 –19A
= 8I3 + 3×4I2A+ 3×2I×A2 +A3 −19A
= 8I + 12IA + 6I×A +A×A2 −19A
= 8I + 18A + A×A −19A
= 8I + A2 −A
= 8I + A−A
= 8I .
18. The Cartesian equation of a line is
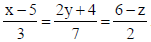
Write its vector equation.
Sol.
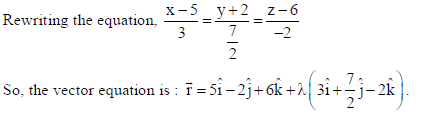
19. If a̅ = 2î – ĵ+ 2k̂ and b̅ = 5î – 3ĵ – 4k̂ , then find the ratio
projection of vector a̅ on vector b̅/ projection of vector b̅ on vector a̅ .
Sol.
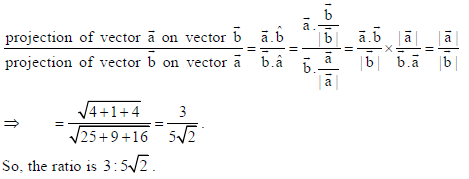
OR
Let â and b̂ be two unit vectors. If the vectors c̅ = â + 2b̂ and d = 5â – 4b̂ are perpendicular to each other, then find the angle between the vectors â and b̂ .
Sol. As c̅ = (â + 2b̂ and d̅ = 5â – 4b̂ are perpendicular so, c̅ .d̅ = 0
That is, (â + 2b̂).(5â – 4b̂) = 0
⇒ 5a2 − 4â .b̂ +10b̂ .â −8b2 = 0 (∵ |â| = a =1 and, |b̂| = b =1
⇒ 6abcosθ = 8×1 − 5×1, where θ is the angle between â and b̂
⇒ 6×1×1×cos θ = 3
⇒ cos θ =3/6
⇒ cos θ = 1/2
∴ θ = π/3 or, 60°
20. Find the particular solution of the differential equation dy/dx = y tan x, when y(0) =1.
Sol. dy/dx = y tan x
⇒ ∫dy/y = ∫tan xdx
⇒ log |y| = log |sec x| + log|C|
⇒ log |y| = log |Csec x|
⇒ y = Csec x
Given that y(0) =1 so, when x = 0 then, y =1.
That is, 1= Csec0 ⇒ 1= C×1 ⇒ C =1.
Therefore, the required particular solution is y = sec x .
SECTION B
Question numbers 21 to 26 carry 2 marks each.
21.

(i) (A+A’) is a symmetric matrix.
(ii) (A – A’) is a skew-symmetric matrix.
Sol.

22. Solve: x dy/dx = y − x cos2 (y/x)
Sol.

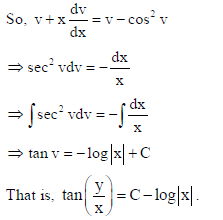
23. Show that | a̅ | b̅ +| b̅ | a̅ is perpendicular to | a̅ | b̅ – | b̅ | a̅, for any two non-zero vectors a̅ and b̅
Sol. {| a̅ | b̅ + | b̅ | a̅}.{| a̅ | b̅ – | b̅ | a̅}
⇒ =| a̅ |2 b̅.b̅− | a̅ || b̅ | b̅.a̅ + | b̅ || a̅ | a̅.b̅− | b̅ |2 a̅.a̅
⇒ =| a̅ |2| b̅ |2 − | a̅ || b̅ | a̅.b̅ + | a̅ || b̅ | a̅.b̅− | b̅ |2| a̅|2
⇒ = 0 .
Hence {| a̅ | b̅+ | b̅ | a̅} ⊥ {| a̅ | b̅ – | b̅ | a̅} as, a̅ and b̅ a̅re non-zero vectors.
24. If y = ex + e−x , then show that

Sol. y = ex + e−x
On squaring both sides, y2 = e2x + e−2x + 2exe−x
That is, y2 = e2x + e−2x + 2
⇒ y2 − 4 = e2x + e−2x − 2
⇒ y2 − 4 = (ex − e−x )2…(i)
Now y = ex + e−x implies, dy/dx = ex + e−x
By (i), we get :

25. Let W denote the set of words in the English dictionary. Define the relation R by
R = {(x, y) ∈ W×W such that x and y have at least one letter in common}.
Show that this relation R is reflexive and symmetric, but not transitive.
Sol. Since (x, x) ∈ R as a word will have ‘all letters in common’ with itself. So, R is reflexive.
Also, if x and y are words with ‘at least one letter in common’ then, we will surely have (x, y) ∈ R as well as (y, x) ∈ R . So, R is symmetric.
Let x be a word ‘Cat’, y be a word ‘Apple’ and z be a word ‘Pen’.
Note that (x, y) ∈ R and (y, z) ∈ R as ‘Cat’ and ‘Apple’ have letter “a” in common and ‘Apple’ and ‘Pen’ have letters “p” and “e” in common.
But (x, z) ∉ R as ‘Cat’ and ‘Pen’ doesn’t have any letter in common.
So, R isn’t transitive.
OR
Find the inverse of the function f (x)= (4x / 3x+4).
Sol.

26. A bag contains 19 tickets, numbered 1 to 19. A ticket is drawn at random and then another ticket is drawn without replacing the first one in the bag. Find the probability distribution of the number of even numbers on the ticket.
Sol. Let X : number of even numbers on the tickets.
So, X can take values 0, 1, 2.
Number of Even tickets in bag are 9 and that of odd tickets are 10.
Number of ways of drawing two tickets = 19C2.
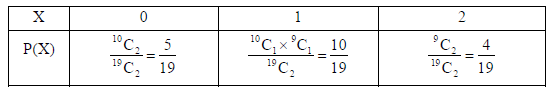
OR
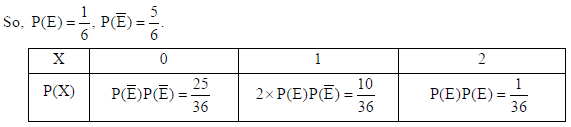
Find the probability distribution of the number of successes in two tosses of a die, when a
success is defined as “number greater than 5”.
Sol. Let X : number of successes in two tosses of a die.
So, X can take values 0, 1, 2.
Here, Success means ‘number greater than 5’.
Let E : number greater than 5 appears on the die.
SECTION C
Question numbers 27 to 32 carry 4 marks each.
27. Prove that
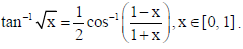
Sol.

28. If â and b̂ are unit vectors inclined at an angle θ , then prove that sinθ/2 = 1/2 | â – b̂ |.
Sol. Consider | â – b̂ |2= (â – b̂).(â – b̂)
⇒| â – b̂ |2 = | â |2 − 2â .b̂ + | b̂ |2
⇒| â – b̂ |2 = 1− 2| â || b̂ | cosθ +1
⇒| â – b̂ |2 = 2 − 2×1×1cos θ
⇒| â – b̂ |2 = 2(1− cosθ)
⇒| â – b̂ |2 = 2 × 2sin2θ/2
That is, sinθ/2 = 1/2 | â – b̂ |.
29. Using properties of determinants, show that

Sol.


OR
Find the equation of the line joining A(1, 3) and B(0, 0) , using determinants. Also, find k if
D(k, 0) is a point such that the area of ΔABD is 3 square units.
Sol.
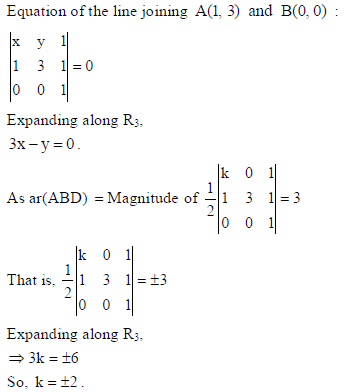
30. A bag contains 5 red and 4 black balls, a second bag contains 3 red and 6 black balls. One of the two bags is selected at random and two balls are drawn at random (without replacement), both of which are found to be red. Find the probability that these two balls are drawn from the second bag.
Sol. Let E1 and E2 be the events that the first bag and second bag is selected, respectively.
Let A : the two balls drawn at random, are both red.

31. Find the shortest distance between the following lines and hence write whether the lines are intersecting or not.

Sol.

OR
Find the equation of the plane through the line of intersection of the planes r̅ .(î + 3ĵ) + 6 = 0 and r̅ .(3î – ĵ – 4k̂ ) = 0, which is at a unit distance from the origin.
Sol.

32. A company produces two types of goods, A and B, that require gold and silver. Each unit of type A requires 3 g of silver and 1 g of gold, while that of type B requires 1 g of silver and 2 g of gold. The company can use at the most 9 g of silver and 8 g of gold. If each unit of type A brings a profit of Rs.120 and that of type B Rs.150, then find the number of units of each type that the company should produce to maximize profit.
Formulate the above LPP and solve it graphically. Also, find the maximum profit.
Sol. Let the number of goods of type A and that of type B be x and y respectively.

SECTION D
Question numbers 33 to 36 carry 6 marks each.
33. If y = 3cos(log x) + 4sin(log x), then show that

Sol. We have y = 3cos (log x) + 4sin(log x)…(i)
On differentiating w.r.t. x both the sides, we get
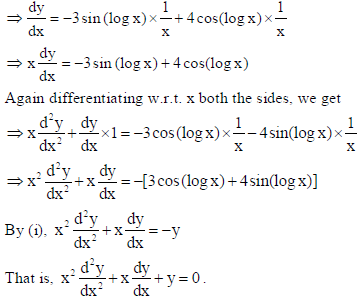
34. Find the intervals in which the function f defined as f (x) = sin x +cos x, 0 ≤ x ≤ 2π is strictly increasing or decreasing.
Sol. We have f (x) = sin x + cos x, 0 ≤ x ≤ 2π⇒ f ‘(x) = cos x −sin x
For f ‘(x) = 0, cos x −sin x = 0
⇒ cos x = sin x
⇒ tan x =1

OR
Prove that the radius of the right circular cylinder of greatest curved surface area which can be inscribed in a given cone is half of that of the cone.
Sol. Let H and R be the height and radius of the base of the given cone respectively.
Suppose the radius and height of the cylinder inscribed in the cone be r and h respectively
Now, BC = DE = r, AB = H – h.

Hence, the radius of the right circular cylinder of greatest curved surface area which can be inscribed in a given cone is half of that of the cone.
35. Evaluate:
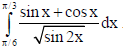
Sol.

36. If the area between the curves x = y2 and x = 4 is divided into two equal parts by the line x = a , then find the value of a using integration.
Sol.

OR
Find:
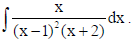
Sol.