Part–A
Section–I

All questions are compulsory. In case of internal choices attempt any one.

Q1. Check whether the function f : R → R defined as f(x) = x³ is one-one or not. 
Answer : Let f(x₁) = f(x₂) for some x₁, x₂ ∈ R
⇒ (x₁)³ = (x₂)³
⇒ x₁ = x₂, hence f(x) is one – one

OR

How many reflexive relations are possible in a set A whose n(A) = 3.
Answer : 26 reflexive relations.

Q2. A relation R in S = {1, 2, 3} is defined as R = {(1, 1), (1, 2), (2, 2), (3, 3)}. Which element(s) of relation R be removed to make R an equivalence relation? 
Answer : (1,2)

Q3. A relation R in the set of real numbers R defined as R = {(a, b): a = b} is a function or not. Justify. 
Answer : Since a is not defined for a ∈ (–∞, 0) ∴ a = b is not a function.

OR

An equivalence relation R in A divides it into equivalence classes A1, A2, A3. What is the value of A1 ∪ A2 ∪ A3 and A1 ∩ A2 ∩ A3.
Answer : A₁ ∪ A₂ ∪ A₃ = A and A₁ ∩ A₂ ∩ A₃ = f

Q4. If A and B are matrices of order 3 × n and m × 5 respectively, then find the order of matrix 5A – 3B, given that it is defined.
Answer : 3 × 5

Q5. Find the value of A², where A is a 2 × 2 matrix whose elements are given by

Answer :

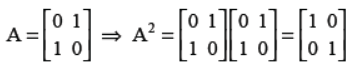
OR 

Given that A is a square matrix of order 3×3 and |A| = –4. Find | adj A |.
Answer : | adj A | = (–4)^3–1 = 16

Q6. Let A = [aij] be a square matrix of order 3 × 3 and |A| = –7. Find the value of a₁₁A₂₁ + a₁₂A₂₂ + a₁₃A₂₃.
where Aij is the cofactor of element a_ij .
Answer : 0

Q7. Find 

Answer : e^x(1 – cot x) + C

OR

Answer : ∵ f(x) is an odd function

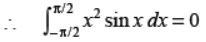
Q8. Find the area bounded by y = x2, the x-axis and the lines x = –1 and x = 1. 
Answer : 

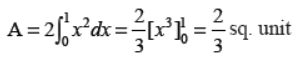
Q9. How many arbitrary constants are there in the particular solution of the differential equation dy/dx = –4xy2; y(0) = 1.
Answer : 0

OR

For what value of n is the following a homogeneous differential equation:
dy/dx = x³–yn /x²y+xy²
Answer : 3

Q10. Find a unit vector in the direction opposite to –3/4 𝑗̂.
Answer : ˆj

Q11. Find the area of the triangle whose two sides are represented by the vectors 2iˆ and − 3𝑗̂.
Answer : 

Q12. Find the angle between the unit vectors aˆ and bˆ , given that | a̅ + b̅| = 1. 
Answer : 

Q13. Find the direction cosines of the normal to YZ plane? 
Answer : 1,0,0

Q14. Find the coordinates of the point where the line x+3/3 = y–1/–1 = z–5/–5 cuts the XY plane.
Answer : (0,0,0)

Q15. The probabilities of A and B solving a problem independently are 1/3 and 1/4 respectively. If both of them try to solve the problem independently, what is the probability that the problem is solved? 
Answer : 

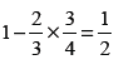
Q16. The probability that it will rain on any particular day is 50%. Find the probability that it rains only on first 4 days of the week.
Answer : 

Section-II

Both the Case study-based questions are compulsory. Attempt any 4 sub-parts from each question (17–18). Each sub-part carries 1 mark.

Q17. An architect designs a building for a multi-national company. The floor consists of a rectangular region with semicircular ends having a perimeter of 200 m as shown below:  

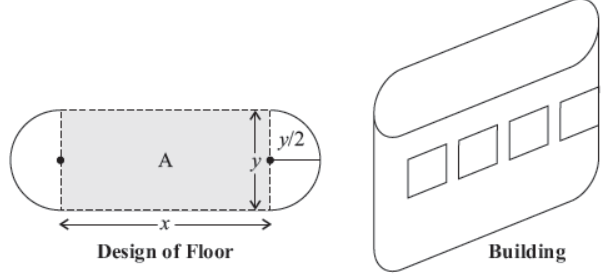
Based on the above information answer the following:

(i) If x and y represents the length and breadth of the rectangular region, then the relation between the variables is 
(a) x + py = 100
(b) 2x + py = 200
(c) px + y = 50
(d) x + y = 100
Answer : B

(ii) The area of the rectangular region A expressed as a function of x is
(a) 2/π (100x–x²)
(b) 1/π (100x–x²)
(c) x/π (100x–x²)
(d) xy² + 2/π (100x–x²)
Answer : A

(iii) The maximum value of area A is
(a) π/3200 m²
(b) π/3200 m²
(c) 5000/π m²
(d) 1000/π m²
Answer : C

(iv) The CEO of the multi-national company is interested in maximizing the area of the whole floor including the semi-circular ends. For this to happen the value of x should be 
(a) 0 m
(b) 30 m
(c) 50 m
(d) 80 m
Answer : A

(v) The extra area generated if the area of the whole floor is maximized is: 
(a) 3000/π m²
(b) 5000/π m²
(c) 7000/π m²
(d) No change, both areas are equal
Answer : D

Q18. In an office three employees Vinay, Sonia and Iqbal process incoming copies of a certain form. Vinay process 50% of the forms. Sonia processes 20% and Iqbal the remaining 30% of the forms. Vinay has an error rate of 0.06, Sonia has an error rate of 0.04 and Iqbal has an error rate of 0.03.

Based on the above information answer the following:

(i) The conditional probability that an error is committed in processing given that Sonia processed the form is: 
(a) 0.0210
(b) 0.04
(c) 0.47
(d) 0.06
Answer : B

(ii) The probability that Sonia processed the form and committed an error is: 
(a) 0.005
(b) 0.006
(c) 0.008
(d) 0.68
Answer : C

(iii) The total probability of committing an error in processing the form is 
(a) 0
(b) 0.047
(c) 0.234
(d) 1
Answer : B

(iv) The manager of the company wants to do a quality check. During inspection he selects a form at random from the days output of processed forms. If the form selected at random has an error, the probability that the form is NOT processed by Vinay is 
(a) 1
(b) 30/47
(c) 20/47
(d) 17/47
Answer : D

(v) Let A be the event of committing an error in processing the form and let E1, E2 and E3 be the events that Vinay, Sonia and Iqbal processed the form. The value of

(a) 0
(b) 0.03
(c) 0.06
(d) 1
Answer : D

Part–B
Section–III

All questions are compulsory. In case of internal choices attempt any one.

Q19. Express tan–1

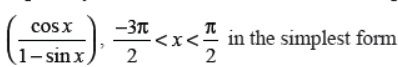
Answer : 

Q20. If A is a square matrix of order 3 such that A² = 2A, then find the value of |A|. 
Answer : A² = 2A
⇒ |AA| = |2A|
⇒ |A| |A| = 8|A| (Q |AB| = |A| |B| and |2A| = 23|A|) 
⇒ |A| (|A| – 8) = 0 
⇒ |A| = 0 or 8

OR

If A  

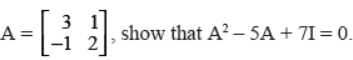
Answer : 

Q21. Find the value(s) of k so that the following function is continuous at x = 0

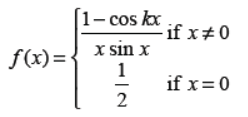
Answer : 

Q22. Find the equation of the normal to the curve y = x + 1/x , x > 0 perpendicular to the line 3x – 4y = 7.
Answer : 

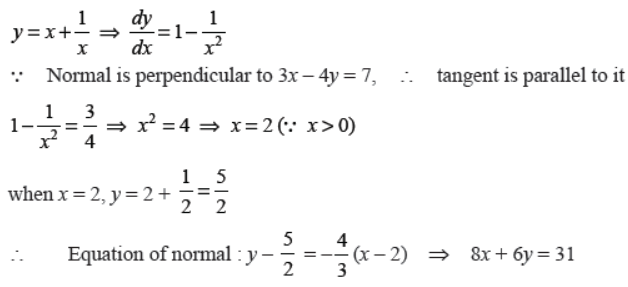
Q23. Find

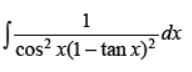
Answer : 

OR

Evaluate
Answer :

Q24. Find the area of the region bounded by the parabola y2 = 8x and the line x = 2. 
Answer : 

Q25. Solve the following differential equation: dy/dx = x3cosec y , given that y(0) = 0.
Answer :

Q26. Find the area of the parallelogram whose one side and a diagonal are represented by coinitial vectors 𝑖̂–𝑗̂+𝑘̂ and 4𝑖̂ + 5𝑘̂ respectively. 
Answer : 

Q27. Find the vector equation of the plane that passes through the point (1, 0, 0) and contains the line r̅ = λj̅ . 
Answer : 

Q28. A refrigerator box contains 2 milk chocolates and 4 dark chocolates. Two chocolates are drawn at random. Find the probability distribution of the number of milk chocolates. What
is the most likely outcome?
Answer : Let x denote the number of milk chocolates drawn

Most likely outcome is getting one chocolate of each type.

OR

Given that E and F are events such that P(E) = 0.8, P(F) = 0.7, P(E ∩ F) = 0.6. Find P (E | F).
Answer : 

Section-IV

All questions are compulsory. In case of internal choices attempt any one.

Q29. Check whether the relation R in the set Z of integers defined as R = {(a, b) : a + b is “divisible by 2”} is reflexive, symmetric or transitive. Write the equivalence class containing 0 i.e. [0].
Answer : (i) Refλexive: Since, a + a = 2a which is even \ (a, a) ∈ R ∀ a ∈ Z
Hence, R is reflexive. 
(ii) Symmetric: If (a, b) ∈ R, then a + b = 2λ ⇒ b + a = 2λ
⇒ (b, a) ∈ R, Hence R is symmetric. 1
(iii) Transitive: If (a, b) ∈ R and (b, c) ∈ R then a + b = 2λ …(1) and b + c = 2m …(2)
Adding (1) and (2) we get a + 2b + c = 2(λ + m)
⇒ a + c = 2(λ + m – b)
⇒ a + c = 2k, where λ + m – b = k
⇒ (a, c) ∈ R
Hence R is transitive 1
[0] = {… –4, –2, 0, 2, 4 …}

Q30. If y = ex² cos x + (sin x)x, find dy/dx.
Answer : 

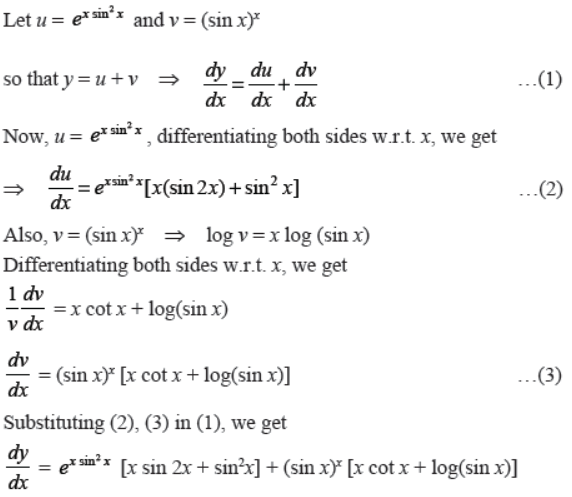
Q31. Prove that the greatest integer function defined by f(x) = [x], 0 < x < 2 is not differentiable at x = 1.
Answer : 

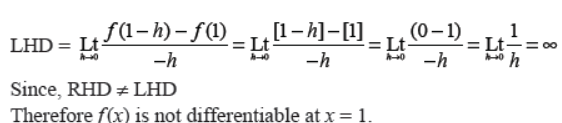
OR

If x = a sec q, y = b tan q, find d²y/dx² at θ = π/2.
Answer : 

Q32. Find the intervals in which the function f given by
f(x) = tan x – 4x , xε (0,π/2) is
(a) strictly increasing
(b) strictly decreasing
Answer : 

Q33. Find

Answer : Put x² = y to make partial fractions

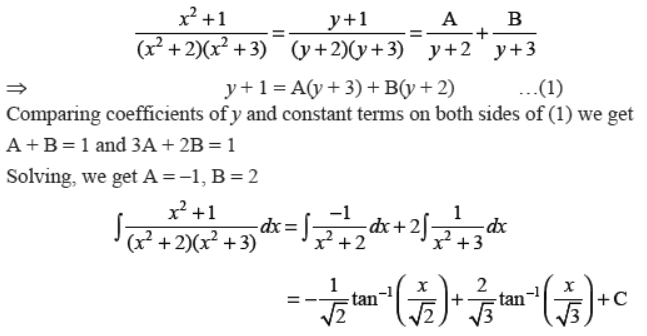
Q34. Find the area of the region bounded by the curves x² + y² = 4, y = 3x and x-axis in the first quadrant.
Answer : Solving y = √3x and x² + y² = 4
We get x² + 3x² = 4
⇒ x² = 1 ⇒ x = 1 

OR

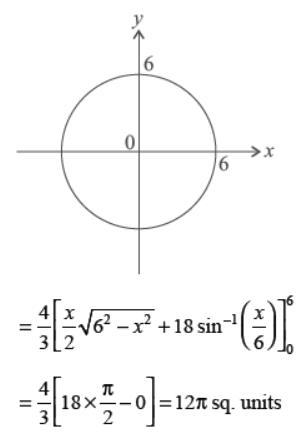
Find the area of the ellipse x2 + 9y2 = 36 using integration.
Answer :  

Q35. Find the general solution of the following differential equation: 
x dy – (y + 2x²)dx = 0
Answer : The given differential equation can be written as 

Section-V

All questions are compulsory. In case of internal choices attempt any one.

Q36. If

x – 2y = 10
2x – y – z = 8
–2y + z = 7
Answer : |A| = 1(–1 – 2) – 2(–2 – 0) = –3 + 4 = 1 
A is nonsingular, therefore A^–1 exists  

OR

Evaluate the product AB, where 

Hence solve the system of linear equations
x – y = 3
2x + 3y + 4z = 17
y + 2z = 7
Answer : 

Q37. Find the shortest distance between the lines
r̅ = 3𝑖̂+2𝑗̂–4𝑘̂ + λ(𝑖̂+2𝑗̂–4𝑘̂)
and r̅ = 5𝑖̂–2𝑗̂+ μ(3𝑖̂+2𝑗̂+6𝑘̂)
If the lines intersect find their point of intersection.
Answer : 

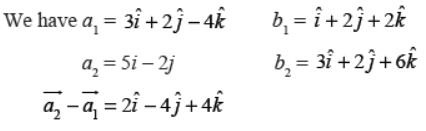
OR

Find the foot of the perpendicular drawn from the point (–1, 3, –6) to the plane
2x + y – 2z + 5 = 0. Also find the equation and length of the perpendicular.
Answer :  Let P be the given point and Q be the foot of the perpendicular.

38. Solve the following linear programming problem (L.P.P.) graphically. 5
Maximize Z = 3x + y subject to constraints;
x + 2y ≥ 100
2x – y ≤ 0
2x + y ≤ 200
x, y ≥ 0
Answer : 

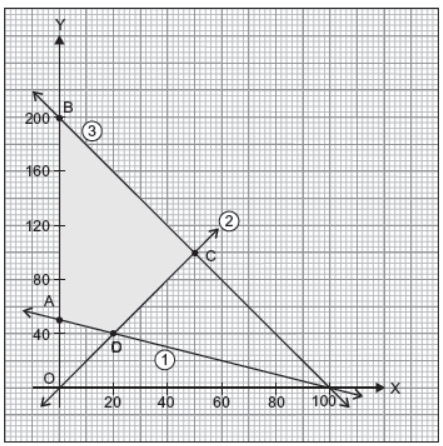
Subject to x + 2y ≥ 100 …(1)
2x – y ≤ 0 …(2)
2x + y ≤ 200 …(3)
x ≥ 0, y ≥ 0

Max z = 250 at x = 50, y = 100

OR

The corner points of the feasible region determined by the system of linear constraints are as shown below:  

Answer each of the following:
(i) Let Z = 3x – 4y be the objective function. Find the maximum and minimum value of Z and also the corresponding points at which the maximum and minimum value occurs.
(ii) Let Z = px + qy, where p, q > 0 be the objective function. Find the condition on p and q so that the maximum value of Z occurs at B(4, 10) and C(6, 8). Also mention the number of optimal solutions in this case.
Answer : 

Max Z = 12 at E(4,0) 1
Min Z = –32 at A(0,8)
(ii) Since maximum value of Z occurs at B(4, 10) and C(6, 8)
∴ 4p + 10q = 6p + 8q
⇒ 2q = 2p
⇒ p = q 2
Number of optimal solutions are infinite.