Students of class 11 Mathematics should refer to MCQ Questions Class 11 Mathematics Relations and Functions with answers provided here which is an important chapter in Class 11 Mathematics NCERT textbook. These MCQ for Class 11 Mathematics with Answers have been prepared based on the latest CBSE and NCERT syllabus and examination guidelines for Class 11 Mathematics. The following MCQs can help you to practice and get better marks in the upcoming class 11 Mathematics examination

Chapter 2 Relations and Functions MCQ with Answers Class 11 Mathematics

MCQ Questions Class 11 Mathematics Relations and Functions with answers provided below have been prepared by expert teachers of grade 11. These objective questions with solutions are expected to come in the upcoming Standard 11 examinations. Learn the below provided MCQ questions to get better marks in examinations.

Question. The figure shows a relation R between the sets P andQ .

The relation R in Set-builder form is
(a) {(x, y):x ∈P, y ∈Q}
(b) {(x, y):x ∈Q, y ∈P}
(c) {(x, y):x is the square of y, x ∈P, y ∈Q}
(d) {(x, y):y is the square of x, x ∈P, y ∈Q}

Question. The values of a and b, if ordered pair is (2a − 5, 4) = (5, b + 6)
(a) −2,5
(b) 2,5
(c) 5, 2
(d) 5, −2

Question. If f (x) = x³ -1/x³ , then f (x) + f(1/x)
(a) 0
(b) 1
(c) 2
(d) not defined

Question. If A = {a₁ , a₂ } and B = {b₁ , b₂ , b₃ , b₄ } , then A × B is equal to
(a) {(a₁,b₁), (a₂, b₂)}
(b) {( a₁,b₁ ), ( a₂, b₂ ), (a₃,b₃), (a₄,b₄)}
(c) {( a₁,b₁ ), ( a₁, b₂ ), ( a₁,b₃ ), (a₁,b₄ )}
(d) {( a₁,b₁ ), ( a₁, b₂ ), ( a₁,b₃ ), (a₁,b₄ ), (a₂,b₁), (a₂,b₂), (a₂,b₃), (a₂,b₄)}

Question. Let n(A) = m and n(B ) = n. Then, the total number of non-empty relations that can be defined from A to B is
(a) mn
(b) nm −1
(c) mn −1
(d) 2 1 mn −

Question. If f (x) = 3x + 10 and g (x) = x ² − 1, then ( fog )−1 is equal to
(a) (x-7 /3)^1/2
(b) (x+7 /3)^1/2
(c) (x-3 /7)^1/2
(d) (x+3 /7)^1/2

Question. Let A = {a, b, c , d} and B = {x, y, z }. What is the number of elements in A × B ?
(a) 6
(b) 7
(c) 12
(d) 64

Question. If A = {1, 2, 3, 4} and B = {5, 6, 7, 8}, then which of the following are relations from A to B?
(a) R1 = {(1,5), (2, 7), (3,8)}
(b) R2 = {(5,2), (3, 7), (4, 7)}
(c) R3 = {(6, 2), (3, 7), (4, 7)}
(d) All are correct

Question. The figure shows a relation R between the sets P andQ .

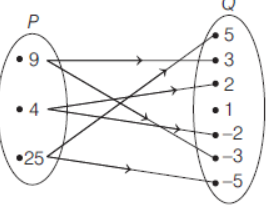
The relation R in Roster form is
(a) {(9, 3), (4, 2), (25, 5)}
(b) {(9, −3), (4, −2), (25, −5)}
(c) {(9, −3), (9, 3), (4, −2), (4, 2), (25, −5), (25, 5)}
(d) None of the above

Question. If y = e^x3 − 2 , then log y at x = 5 is
(a) 321
(b) 234
(c) 125
(d) 123

Question. If a relation R is defined on the set Z of integers as follows
(a, b ) ∈R Ûa 2 + b 2 = 25, then domain (R) is equal to
(a) {3,4,5}
(b) {0, 3,4,5}
(c) {0, ± 3, ± 4, ± 5}
(d) None of these

Question. Let A = {1, 2, 3, 4} andB = {1, 4, 9, 16, 25} and R be a relation defined from A to B, as R = {(x, y ):x ∈A, y∈B and y = x 2 }, then domain of R and codomain of R is
(a) {1, 2, 3, 4} and {1, 4, 9, 16, 25}
(b) {1, 4, 9, 16, 25} and {1, 2, 3, 4}
(c) {1, 2, 3, 4} and {1, 2, 3, 4, 9, 16, 25}
(d) None of the above

Question. The domain of the function f , defined by f (x)
(a) R
(b) R+
(c) R−
(d) None of these

Question. Which of the following is an ordered pair?
(a) (p,q), p ∈P andq ∈Q
(b) [p,q], p ∈P andq ∈Q
(c) {p,q}, p ∈P andq ∈Q
(d) All of the above

Question. The inverse of the function
f (x) = log a (x + √x 2 + 1)
(where, a < 0,a ¹ 1) is
(a) 1/2 (ax – ax ) 
(b) not defined for all x
(c) defined for x >0
(d) None of the above

Question. Is the given relation a function?
{(3, 3), (4, 2), (5, 1), (6, 0), (7, 7)}
(a) Yes
(b) No
(c) cannot say
(d) Insufficient data

Question. The range of the function f (x) = x/1+x2
(a) (−∞,∞)
(b) [−1,1]
(c) [-1/2 ,1/2]
(d) [ −2, 2]

Question. There are three relations R1, R2 and R3 such that R1 = {(2, 1), (3, 1)(4, 2)},
R2 = {(2, 2), (2, 4), (3, 3), (4, 4)} and
R3 = {(1, 2), (2, 3), (3, 4), (4, 5), (5, 6), (6, 7)}.
Then,
(a) R1 and R2 are functions
(b) R2 and R3 are functions
(c) R1 and R3 are functions
(d) Only R1 is a function

Question. If A × B = {(a, 1), (b, 3), (a, 3),
(b, 1), (a, 2), (b, 2)}. Then, A and B is
(a) A = {1, 3,2} and B = {a,b }
(b) A = {a,1,2} and B = {b, 3}
(c) A = {a,b } and B = {1,2, 3}
(d) A = {a,b,1} and B = {a,b,2, 3}

Question. Domain of √a2 − x2 (a> 0)is
(a) (−a,a)
(b) [−a,a]
(c) [0,a]
(d) (−a,0]

Question. f : R − {3} → R be defined by f (x) = x2-9/x-3 and g : R → R be defined by g (x ) = x + 3. Then, f (x ) and g (x ) are
(a) Equal functions
(b) not equal (domains are same)
(c) not equal (domains are not same)
(d) None of the above

Question. The domain and range of the real function f defined by f (x)
4-x /x-4 is given by
(a) Domain = R, Range = {−1,1 }
(b) Domain = R − { 1 }, Range = R
(c) Domain = R − {4}, Range = R − {−1 }
(d) Domain = R − {−4}, Range = {−1,1 }

Question. If A = {1, 2, 6} and R be the relation defined on A by R = {(a,b ):a∈A,b ∈A and a divides b}, then range of R is equal to
(a) {1, 2}
(b) {2, 6}
(c) {1, 2, 6}
(d) None of these

Question. The domain and range of the function f given by f (x) = 2 − | x − 5| is
(a) Domain = R+ , Range = (−∞,1]
(b) Domain = R, Range = (−∞,2]
(c) Domain = R, Range = (−∞,2)
(d) Domain = R+ , Range = (−∞,2]

Question. IfG represents the name of the function in above graph, then G is a/an

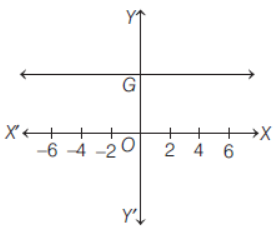
(a) identity function
(b) constant function
(c) modulus function
(d) None of the above

Question. If A = {1, 2, 5, 6} and B = {1, 2, 3}, then what is (A × B ) Ç (B × A) equal to?
(a) {(1,1), (2,1), (6,1), (3,2)}
(b) {(1,1), (1,2), (2,1), (2,2)}
(c) {(1,1), (2,2)}
(d) {(1,1), (1,2), (2,5), (2, 6)}

Question. For each non-zero real number x,
let f (x) =x/|x|
The range of f is
(a) a null set
(b) a set consisting of only one element
(c) a set consisting of two elements
(d) a set consisting of infinitely many elements

Question.

Which of the following options identify the above graph?
(a) Modulus function
(b) Greatest integer function
(c) Signum function
(d) None of the above

Question. If [x]² – 5[x] + 6 =0 , where [ . ] denote the greatest integer function, then
(a) x ∈[3,4]
(b) x ∈(2, 3]
(c) x ∈[2, 3]
(d) x ∈[2,4)

Question. If f (x) = loge (1+x/1-x) then f (2/1+x²) is equal to
(a) [f(x)]2
(b) [f(x)] 3
(c) 2f(x)
(d) 3 f(x)

Question. Method to Find the Sets When Cartesian Product is Given
For finding these two sets, we write first element of each ordered pair in first set say A and corresponding second element in second set B (say).
Number of Elements in Cartesian Product of Two Sets
If there are p elements in set A and q elements in set B, then there will be pq elements in A × B i.e. if n (A) = p and n (B ) = q, then n (A × B ) = pq.
Based on the above two topic, answer the following questions.

(i) If A × B = {(a, 1), (b, 3), (a, 3), (b, 1), (a, 2), (b, 2)}. Then, A and B are
(a) {1, 3, 2}, {a,b }
(b) {a,b },{1,3}
(c) {a,b },{1,3,2}
(d) None of these

(ii) If the set A has 3 elements and set B has 4 elements, then the number of elements in A × B is
(a) 3
(b) 4
(c) 7
(d) 12

(iii) A and B are two sets given in such a way that A × B contains 6 elements.
If three elements of A × B are (1, 3), (2, 5) and (3, 3), then A, B are
(a) {1, 2, 3}, {3, 5}
(b) {3, 5,}, {1, 2, 3}
(c) {1, 2}, {3, 5}
(d) {1, 2, 3}, {5}

(iv) The remaining elements of A × B in (iii) is
(a) (5, 1), (3, 2), (3, 5)
(b) (1, 5), (2, 3), (3, 5)
(c) (1, 5), (3, 2), (5, 3)
(d) None of the above

(v) The cartesian product P × P has 16 elements among which are found (a,1) and (b, 2). Then, the set P is
(a) {a,b }
(b) {1, 2}
(c) {a,b,1,2}
(d) {a,b,1,2,4}

Question. Ordered Pairs The ordered pair of two elements a and b is denoted by (a, b ) : a is first element (or first component) and b is second element (or second component).
Two ordered pairs are equal if their corresponding elements are equal.
i.e. (a, b ) = (c , d ) Þ a = c and b = d Cartesian Product of Two Sets For two non-empty sets A and B, the cartesian product A × B is the set of all ordered pairs of elements from sets A and B.
In symbolic form, it can be written as A × B = {(a, b ) : a ÎA, b ÎB}
Based on the above topics, answer the following questions.
(i) If (a − 3, b + 7) = (3, 7), then the value of a and b are
(a) 6, 0
(b) 3, 7
(c) 7, 0
(d) 3, −7

(ii) If (x + 6, y − 2) = (0, 6), then the value of x and y are
(a) 6, 8
(b) − 6,−8
(c) −6,8
(d) 6,−8

(iii) If (x + 2, 4) = (5, 2x + y ), then the value of x and y are
(a) −3 2 ,
(b) 3, 2
(c) −3,−2
(d) 3,−2

(iv) Let A and B be two sets such that A × B consists of 6 elements. If three elements of A × B are (1, 4), (2, 6) and (3, 6), then
(a) (A ×B) = (B × A)
(b) (A ×B) ¹ (B × A)
(c) A ×B = {(1,4), (1, 6), (2,4)}
(d) None of the above

(v) If n(A × B ) = 45, then n(A) cannot be
(a) 15
(b) 17
(c) 5
(d) 9

Assertion & Reasoning Based Questions :

(a) Assertion and Reason both are correct statements and Reason is the correct explanation of Assertion.
(b) Assertion and Reason both are correct statements but Reason is not the correct explanation of Assertion.
(c) Assertion is correct statement but Reason is wrong statement.
(d) Assertion is wrong statement but Reason is correct statement.

Question. Assertion : The value of sin(–690°) cos(–300°) + cos(–750°)sin(–240°) = 1
Reason : The values of sin and cos is negative in third and fourth quadrant respectively.

Question. Assertion : The value of θ = π/3 or 2π/3 , when q lies between (0, 2θ) and sin2θ = 3/4
Reason : sinq is positive in the first and second quadrant. 

Question. Let secq + tanθ = m, where 0 < m < 1.
Assertion : secq = m² + 1/2m and sinq = m2 + 1/m² + 1
Reason : θ lies in the third quadrant.

Question. If A + B + C = 180°, then Assertion : cos2 A/2 + cos2 B/2 – cos2 C/2 = 2cos A/2 cos B/2 sin C/2
Reason : cos C + cosD = 2cos (C + D/2) cos (C – D/2)

Question. Let a be a real number lying between 0 and π/2 and n be a positive integer.
Assertion : tanα + 2tan2α + 22tan22α + … + 2n–1 tan2n–1 α + 2n cot 2n α = cota.
Reason : cotα – tanα = 2cot2α.

We hope the above MCQ Questions Class 11 Mathematics Relations and Functions with answers based on the latest syllabus and examination guidelines issued by CBSE, NCERT and KVS are really useful for you. Relations and Functions is an important chapter in Class 11 as it provides very strong understanding about this topic. Students should go through the answers provided for the MCQs after they have themselves solved the questions. All MCQs have been provided with four options for the students to solve. These questions are really useful for benefit of class 11 students. Please go through these and let us know if you have any feedback in the comments section.