MCQs for Mathematics Class 11 with Answers Chapter 5 Complex Numbers and Quadratic Equations
Students of class 11 Mathematics should refer to MCQ Questions Class 11 Mathematics Complex Numbers and Quadratic Equations with answers provided here which is an important chapter in Class 11 Mathematics NCERT textbook. These MCQ for Class 11 Mathematics with Answers have been prepared based on the latest CBSE and NCERT syllabus and examination guidelines for Class 11 Mathematics. The following MCQs can help you to practice and get better marks in the upcoming class 11 Mathematics examination
Chapter 5 Complex Numbers and Quadratic Equations MCQ with Answers Class 11 Mathematics
MCQ Questions Class 11 Mathematics Complex Numbers and Quadratic Equations with answers provided below have been prepared by expert teachers of grade 11. These objective questions with solutions are expected to come in the upcoming Standard 11 examinations. Learn the below provided MCQ questions to get better marks in examinations.
Question.The number of complex numbers z such that
|z -1| = |z +1| = |z -i| , is
(a) 0
(b) 1
(c) 2
(d) ∞
Answer
B
Question: If the roots of the equation α/x-α+ β/x-β = 1 be equal in magnitude but opposite in sign, then α +β+ is equal to
(a) 0
(b) 1
(c) 2
(d) None of these
Answer
A
Question:
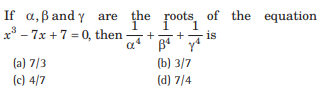
Answer
B
Question: The least value of |a| for which tan Φ and cot Φ are roots of the equation x2+ax+1=0, is
(a) 2
(b) 1
(c) 1/2
(d) 0
Answer
A
Question: The harmonic mean of the roots of the equation
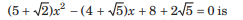
(a) 2
(b) 4
(c) 6
(d) 8
Answer
B
Question: If the roots of the equation 1/x+p +1/x+q =1/r are equal in magnitude but opposite in sign, then the product of the roots will be
(a) p2+q2/2
(b) -(p2+q2)/2
(c) p2-q2/2
(d) -(p2-q2)/2
Answer
B
Question: If x1, x2 and x3 are distinct roots of the equation ax2+bx+c=0,then
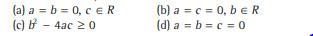
Answer
D
Question:
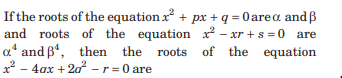
(a) both negative
(b) both positive
(c) both real
(d) one negative and one positive
Answer
C
Question: If x2+2x+2xy+my-3=0 has two rational factors,
then the values of m will be
(a) -6- 2
(b) – 6,2
(c) 6, -2
(d) 6, 2,
Answer
C
Question: If a+ b+ c = 0, then the roots of the equation
4ax2+3bx+2c=0 are
(a) equal
(b) imaginary
(c) real
(d) None of these
Answer
C
Question: If a<b<c< d, then the roots of the equation
(x-a)(x-c) +2(x-d)=0 = 2 0 are
(a) real and distinct
(b) real and equal
(c) imaginary
(d) None of these
Answer
A
Question: If the roots of the equation qx2+ px+ q =2
are complex, where p q and are real, then the roots of the
equation x2-4qx+ p2=0 are
(a) real and unequal
(b) real and equal
(c) imaginary
(d) None of these
Answer
A
Question. If a complex number z satisfies the equation
z +√2 z +1 + i = 0, then z is equal to j JEE Mains 2013
(a) 2
(b) √3
(c) √5
(d) 1
Answer
C
Question. If the imaginary part of (2z +1) / (iz +1) is -2, then the locus of the point representing z in the complex plane is
(a) a circle
(b) a straight line
(c) a parabola
(d) None of these
Answer
B
Question. If z z + (3 – 4i )z + (3 + 4i )z = 0 represent a circle, the area of the circle in square units is
(a) 5p
(b) 10p
(c) 25 p2
(d) 25p
Answer
D
Question. If a and b are two different complex numbers such that |α|=1.|β| =1
(a) 3 + 1
(b) 5 + 1
(c) 2
(d) 2 + 2
Answer
B
Question. If a , band c are integers not all equal and w is a cube root of unity (where, w ¹1), then minimum value of |a + bw + cw2 | is equal to
(a) 0
(b) 1
(c) √3/2
(d) 1/2
Answer
B
Question. If | z | , | z | 1 2 = 2 = 3 then z z i 1 2 + + 5 +12 is less than or equal to
(a) 8
(b) 18
(c) 10
(d) 5
Answer
B
Question. If z < 3 -1, then z z 2 + 2 cos a is
(a) less than 2
(b) 3 + 1
(c) 3 – 1
(d) None of these
Answer
A
Question. Number of solutions of the equation z z 2 + 7 = 0 is/are
(a) 1
(b) 2
(c) 4
(d) 6
Answer
B
Question. Let z and w are two non-zero complex numbers such that |z| = |ω| and arg z + arg w = ω, then z equals
(a) ω
(b) ω
(c) -ω
(d) -ω
Answer
C
Question. If |z -1| =1, then arg (z ) is equal to
(a)1/2 arg (z)
(b) 1/3 arg (z + 1)
(c) 1/2 arg (z – 1)
(d) None of these
Answer
C
Question. If w(¹1) is a cube root of unity and (1 )+ w 7 = A + Bw.
Then, (A, B) is equal to
(a) (1,1)
(b) (1, 0)
(c) (-1, 1)
(d) (0, 1)
Answer
A
Question. If a,b ÎC are the distinct roots of the equation x2 – x +1 = 0, then α101 + β107 is equal to
(a) -1
(b) 0
(c) 1
(d) 2
Answer
C
Question. If Re (1/z) = 3, then z lies on
(a) circle with centre onY-axis
(b) circle with centre on X-axis not passing through origin
(c) circle with centre on X-axis passing through origin
(d) None of the above
Answer
C
Question. If | z2 | | z |2 = +1, then z lies on
(a) a real axis
(b) an ellipse
(c) a circle
(d) imaginary axis
Answer
D
Question. Let z satisfy z =1 and z =1- z j
Statement I z is a real number.
Statement II Principal argument of z is p /3.
(a) Statement I is true, Statement II is true; Statement II is a correct explanation for statement I
(b) Statement I is true, Statement II is true; Statement II is not a correct explanation for Statement I
(c) Statement I is true, Statement II is false
(d) Statement I is false, Statement II is true
Answer
D
Question. If | z | =1 and z ≠ ± 1, then all the values of z/1-z2 lie on
(a) a line not passing through the origin
(b) | z | = √2
(c) the X-axis
(d) the Y-axis
Answer
D
Question. If 4x + i(3x − y ) = 3 + i(−6), where x and y are real numbers, then the values of x and y are
(a) x = 3 , y =4
(b) x = 3/4 , y = 33/4
(c) x =4, y = 3
(d) x = 33 , y =4
Answer
B
Question. If i a ib 103 = + , then a + b is equal to
(a) 1
(b) −1
(c) 0
(d) 2
Answer
B
Question. 1 + i10 + i 20 + i30 is a
(a) Real number
(b) Complex number
(c) Natural number
(d) None of these
Answer
A
Question. The value of i4x 1 i4x 1 /2 is equal to
(a) i
(b) −1
(c) −i
(d) 0
Answer
A
Question. The multiplicative inverse of 3+5i/4-3i is equal to
(a) 3/34 -29/34i
(b) 3/34 +29/34i
(c) 3/34 – 29/34i
(d)−1/34 -29/34i
Answer
A
Question. If z1 = 2 + 3i and z2 = 3 + 2i, then z1 + z2 + equals to
(a) 5 + 5 i
(b) 5 + 10i
(c) 4 + 6 i
(d) 6 + 4i
Answer
A
Question. The modulus of the complex number4 + 3i7 is equal to
(a) 5
(b) −5
(c) 2
(d) 3
Answer
A
Question. If z i 1 = 2 + 3 and z2 = 3 − 2i, then z1 z2 − is equal to
(a) −1 + 5i
(b) 5 −i
(c) i + 5
(d) None of these
Answer
A
Question. If (−i )(3i)(1-6i)3 =a+ib then a is equal to
(a) 1
(b) 0
(c) −1
(d) 2
Answer
B
Question. If Zi = 2 + 3i and Z2 = 1 − 4i then Z1Z2 is equal to
(a) 14 −5i
(b) 14 + 5i
(c) −14 + 5i
(d) −14 −5i
Answer
A
Question. If 3(7 + 7i ) + i(7 + 7i ) = a +ib then b/a is equal to
(a) 2
(b) 1
(c) 3
(d) −1
Answer
A
Question. If (1+i)2 /2-i = x+iy then the value of x + y is
(a) 1/5
(b) 2/5
(c) 3/5
(d) 4/5
Answer
B
Question. If (1 − i )4 = a + ib, then the value of a and b are respectively
(a) −4,0
(b) 0, −4
(c) 4,0
(d) 0,4
Answer
A
Question. If z1 = 6 + 3i and z2 = 2 −i, then z1/z2 is equal to
(a) 1/5 (9 +12i)
(b) 9 + 12i
(c) 3 + 2i
(d) 1/5 (12+9i)
Answer
A
Question. If Z1 = √3 +√3i and Z2 = √3 +i then the quadrant in which (Z1/Z2) lies is
(a) First
(b) Second
(c) Third
(d) Fourth
Answer
A
Question. If (1 − i )x +(1 + i )y = 1 − 3i, then (x, y ) is equal to
(a) (2, −1)
(b) (−2,1)
(c) (−2, −1)
(d) (2,1)
Answer
A
Question. If Z1 i = 1 + 2 and Z2 = 2 + 3i, then sum of Z1 and additive inverse of Z2 is equal to
(a) 1 + 2i
(b) 3 + i
(c) 3 + 5i
(d) −1 −i
Answer
D
Question. If difference in roots of the equation x2 – px + 8 = 0 is 2, then p is equal to
(a) ± 6
(b) ± 2
(c) ± 1
(d) ± 5
Answer
A
Question. If Z1/Z1+Z2 = 3 + 2i and Z2 = 2 − i then
(a) 5 −i
(b) 5 +i
(c) −5 + i
(d) −5 −i
Answer
A
Question. If Zi/Z1Z2 = 1 + , Z2 = 2 − i and a ib = + , then a + b is equal to
(a) 2
(b) 1
(c) 3
(d) 4
Answer
A
Question. If Z1 = 3 + 2i and Z2 = 2 − 4i then the value of |z 1 + z 2 | |z1 – z2 |2 is equal to
(a) 11
(b) 22
(c) 66
(d) 55
Answer
C
Question. The conjugate of 2-i/(1-2i)2 is equal to
(a) −2/25 + 11/25i
(b) −2/25 + 11/25i
(c) 2/25 + 11/25i
(d) 2/25 – 11/25i
Answer
B
Question. Let Z1 = 2 – i and Z2 = -2, then (Z1Z2/Z1) = + , then a is equal to
(a) 2/5
(b) 3/5
(c) 11/5
(d) −2/5
Answer
D
Question. Let Z1 = 3 + 5i and Z2 = 2 – 3i, then (Z1Z2/Z1) = + , then a is equal to
(a) 9/13 +19/13i
(b) 9/13 -19/13i
(c) −9/13 -19/13i
(d)−9/13 +19/13i
Answer
D
Question. If Z i 1 = 1 + 3 and Z2 = 2 + 4i then |Z2 – Z1|−2 is equal to
(a) 1
(b) 2
(c) 3
(d) 4
Answer
B
Question. a + ib form of complex number 9 −i + 6 + i3 − 9 +i2 is given by
(a) 7 −2i
(b) 7 + 2i
(c) −7 −2i
(d) −7 + 2i
Answer
B
Question. If Z = (1+i)(2+i)/(3+i) then|Z| is equal to
(a) 1
(b) 0
(c) 2
(d) 3
Answer
A
Question. The modulus of the complex number (1 − i)−2 + (1 +i)−2is equal to
(a) 1
(b) 0
(c) 2
(d) 3
Answer
D
Question. The modulus of the complex number (1 −i)−2 + (1 +i)−2 i i is equal to
(a) 1
(b) 2
(c) 3
(d) 0
Answer
D
Question. Roots of 9x2 + 16 = 0is given by
(a) ± (4/3)i
(b) ± (3/4)i
(c) ± (3/2)i
(d) ± (2/3)i
Answer
A
Question. Roots of x2 + 2 = 0 are
(a) ± √2i
(b) 2
(c) 2i
(d) None of these
Answer
A
Question. Roots of x2 + 3x + 9 = 0 are
(a) (-3±3√3i)/2
(b) (3±3√3i)/2
(c) (3±√3i)/2
(d) (-3±√3i)/2
Answer
A
Question. Roots of x2 + + 1 = 0 are
(a) (-1±√3i)/2
(b) (1±√3i)/2
(c) (2±√3i)/2
(d) (-2±√3i)/2
Answer
A
Question. Roots of √2x2 + x + √2 = is given by
(a) (-1±√7i)/2√2
(b) (-1±√7i)/√2
(c) (1±√7i)/√2
(d) None of these
Answer
A
Question. Roots of (y + 1)(y − 3) + 7 = 0 is given by
(a) (-1±√3i)
(b) (1±√3i)
(c) (1±√2i)
(d) (-1±√2i)
Answer
B
Question. Two complex numbers Z a ib 1 = + and Z2 c id = + are said to be equal, if a = c and b = d.
On the basis of above information, answer the following questions.
(i) If (3a − 6) + 2ib = − 6b + (6 + a)i, then the real values of a and b are respectively
(a) −2, 2
(b) 2,−2
(c) 3, −3
(d) 4, 2
Answer
A
(ii) If (2a + 2b ) + i (b − a) = − 4i, then the real values of a and b are respectively.
(a) 2, 3
(b) 2, −2
(c) 3, 1
(d) −2,2
Answer
B
(iii) If (1-i/1+i) a ib, then the values of a and b are respectively
(a) 1, 0
(b) 0, 1
(c) 1, 2
(d) 2, 1
Answer
A

We hope the above MCQ Questions Class 11 Mathematics Complex Numbers and Quadratic Equations with answers based on the latest syllabus and examination guidelines issued by CBSE, NCERT and KVS are really useful for you. Complex Numbers and Quadratic Equations is an important chapter in Class 11 as it provides very strong understanding about this topic. Students should go through the answers provided for the MCQs after they have themselves solved the questions. All MCQs have been provided with four options for the students to solve. These questions are really useful for benefit of class 11 students. Please go through these and let us know if you have any feedback in the comments section.
