PART – A
Section – I

1. A random variable X has the following distribution.

X	1	2	3	4	5	6	7	8
P(X)	0.15	0.23	0.12	0.10	0.20	0.08	0.07	0.05

For the event E = {X is a prime number}, find P(E).
Answer : P(E) = P(X = 2) + P(X = 3) + P(X = 5) + P(X = 7)
= 0.23 + 0.12 + 0.20 + 0.07 = 0.62

OR

If A and B are two events such that P(A|B) = p, P(A) = 1/3, P(B)= P(A∪B)= 5/9 and then find the value of p.
Answer : 

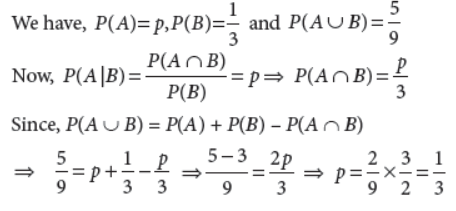
2. If A and B are the points (– 3, 4, – 8) and (5, – 6, 4) respectively, then find the ratio in which yz-plane divides AB.
Answer : 

3. If

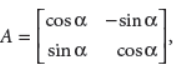
 then for what value of α, A is an identity matrix?
Answer : 

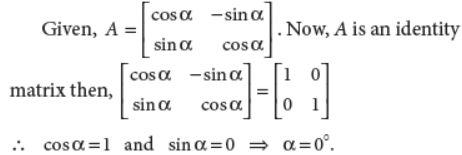
OR

If

 then find the matrix PQ.
Answer : 

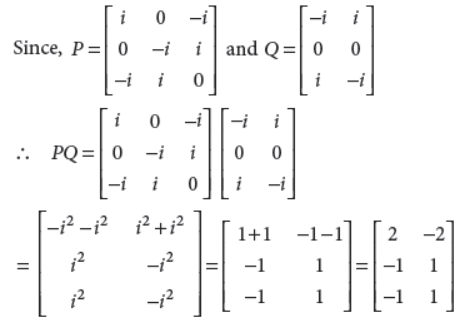
4. Find the distance of the point (2, 3, 4) from the plane r̄.(3î−6ĵ+2k̂)+11=0
Answer : Here,ā = 2î+3ĵ+4k̂
The distance of the point (2î+3ĵ+4k̂)

5. Evaluate : 

Answer : 

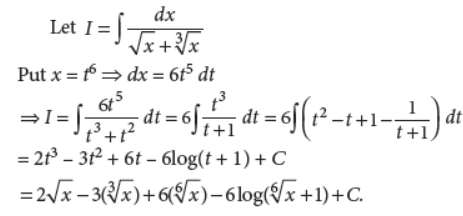
OR

Evaluate :

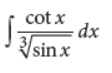
Answer : 

6. Prove that the area bounded by the parabola y2 = 4ax and the line x = a and x = 4a is 56a²/3 sq. units.
Answer : Required area = 2 × area of region PSRQP

7. If the position vector ā of a point (12, n) is such that |ā| , a = 13 then find the value of n .
Answer : The position vector of the point (12, n) is 12î + nĵ.

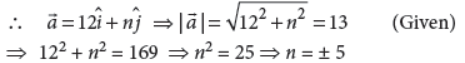
OR

Find the projection of vector 7î+ĵ−4k̂ on the vector 2î+6ĵ+3k̂
Answer : 

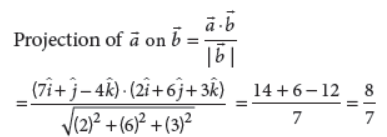
8. Find the value of l for which the vectors 3î−6ĵ+k̂ and 2î−4ĵ+λk̂are parallel.
Answer : 

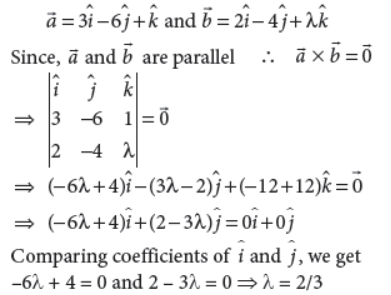
9. The number of bijective functions from the set A to itself, if A contains 108 elements is n!. Find the value of n. 
Answer : Since number of one-one onto functions from a set A having n elements to itself is n!. 
∴ Required value of n is 108.

OR

If the set A contains 5 elements and the set B contains 6 elements, then find the number of one-one and onto mappings from A to B.
Answer : As A contains 5 elements.
∴ For any one-one onto mapping f : A → B, f (A) also contains 5 elements but B contains 6 elements.
∴ f (A) ≠ B.
So, no one-one mapping from A to B can be onto.

10. Find the order of the differential equation whose general solution is given by y = (A + B) cos (x + C) + Dex.
Answer : Given y = (A + B) cos (x + C) + Dex
or y = k cos (x + C) + Dex
Now order of a differential equation is same as the number of arbitrary unknowns present in the solution.
Hence order of differential equation is 3.

11. Construct a 2 × 3 matrix whose elements aij are given by aij = 2i – 3j.
Answer : Here aij = 2i – 3j, i = 1, 2 and j = 1, 2, 3
∴ a₁₁ = 2⋅1 – 3⋅1 = –1, a₁₂ = 2⋅1 – 3⋅2 = – 4,
a₁₃ = 2⋅1 – 3⋅3 = – 7, a21 = 2⋅2 – 3⋅1 = 1,
a₂₂ = 2⋅2 – 3⋅2 = – 2, a₂₃ = 2⋅2 – 3⋅3 = – 5
Hence, the required matrix is

12. The random variable X has the following probability distribution :

Find the value of k.
Answer : 

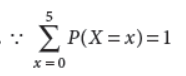
⇒ P(X = 0) + P(X = 1) + …. + P(X = 5) = 1
⇒ 0.1 + k + 0.1 + 3k + 0.3 + k = 1 ⇒ 0.5 + 5k = 1
⇒ 5k = 1 – 0.5 = 0.5 ⇒ k = 0.1

13. Find the range of the function f(x) = |x-1|/(x-1).
Answer : 

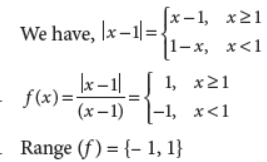
14. For what value of x, matrix

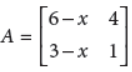
 is a singular matrix?
Answer : Matrix A is singular, when |A| = 0

15. Let R be a relation on the set N be defined by {(x, y) : x, y ∈N, 2x + y = 41}. Show that R is neither reflexive nor symmetric.
Answer : R = {(x, y) : x, y ∈N, 2x + y = 41}
Reflexive : (1, 1) ∉ R as 2 ⋅ 1 + 1 = 3 ≠ 41. So, R is not reflexive.
Symmetric : (1, 39) ∈R but (39, 1) ∉ R. So R is not symmetric.

16. Write the direction cosines of a line parallel to the line 3-x/3 = y+2/-2 = z+2/6.
Answer : 

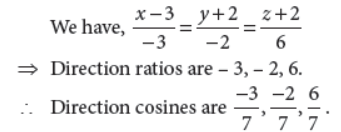
These are direction cosines of a line parallel to given line.

Section – II

Case study-based questions are compulsory. Attempt any 4 sub parts from each question. Each sub-part carries 1 mark.

17. In a school, a football game is to be organised between students of class 11th and 12th. For which, a team from each class is chosen, say T1 be the team of class 11th and T2 be the team class 12th. These teams have to play two games against each other. It is assumed that the outcomes of the two games are independent. The probability of T1 winning, drawing and losing a game against T2 are 1/2 , 1/6 and 1/3 respectively.   

Each team gets 3 points for a win, 1 point for a draw and 0 point for a loss in a game.
Let X and Y denote the total points scored by team T1 and T2, respectively, after two games.
Based on the above information answer the following :

(i) P(T2 winning a match against T1) is equal to
(a) 1/2
(b) 1/6
(c) 1/3
(d) none of these
Answer : C

(ii) P(T2 drawing a match against T1) is equal to
(a) 1/2
(b) 1/3
(c) 1/6
(d) 2/3
Answer : C

(iii) P(X > Y) is equal to
(a) 1/4
(b) 5/12
(c) 1/2
(d) 7/12
Answer : B

(iv) P(X = Y) is equal to
(a) 11/36
(b) 1/3
(c) 13/36
(d) 1/2
Answer : C

(v) P(X + Y = 12) is equal to
(a) 0
(b) 5/12
(c) 13/36
(d) 7/12
Answer : A

18. Mr. Vinay is the owner of apartment complex with 50 units. When he set rent at ₹ 8000/month, all apartments are rented. If he increases rent by ₹ 250/month, one fewer apartment is rented.
The maintenance cost for each occupied unit is ₹ 500/month.
Based on the above information answer the following :

(i) If P is the rent price per apartment and N is the number of rented apartment, then profit is given by
(a) NP
(b) (N – 500)P
(c) N(P – 500)
(d) none of these
Answer : C

(ii) If x represent the number of apartments which are not rented, then the profit expressed as a function of x is
(a) (50 – x) (30 + x)
(b) (50 + x) (30 – x)
(c) 250(50 – x) (30 + x)
(d) 250(50 + x) (30 – x)
Answer : C

(iii) If P = 8500, then N =
(a) 50
(b) 48
(c) 49
(d) 47
Answer : B

(iv) If P = 8250, then the profit is
(a) ₹ 379750
(b) ₹ 4,00,000
(c) ₹ 4,05,000
(d) ₹ 4,50,000
Answer : A

(v) The rent that maximizes the total amount of profit is
(a) ₹ 5000
(b) ₹ 10500
(c) ₹ 14800
(d) ₹ 14500
Answer : B

PART – B
Section – III

19. Find the value of ‘a’ if the function f(x) defined by

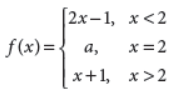
 is continuous at x = 2.
Answer : For f to be continuous at x = 2, we must have

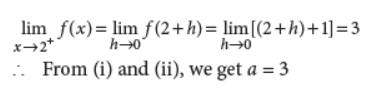
20. Evaluate : ∫x²(a+b)^-2dx
Answer : 

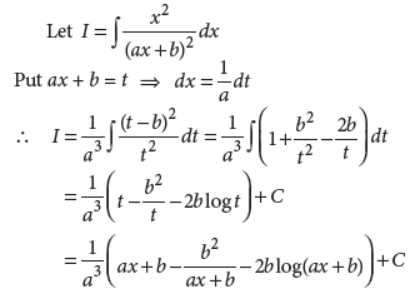
OR

Evaluate :  

Answer : 

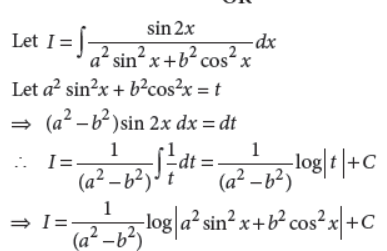
21. Find the area bounded by the line y = x, x-axis and lines x = –1 to x = 2.
Answer : We have, y = x

22. If A 

Answer : 

23. A machine produces parts that are either good (90%), slightly defective (2%), or obviously defective (8%).
Produced parts get passed through an automatic inspection machine, which is able to detect any part that is obviously defective and discard it. What is the probability of the parts that make it through the inspection machine and get shipped?
Answer : Let G, SD, OD be the events that a randomly chosen part is good, slightly defective, obviously defective respectively.
Then, P(G) = 0.90, P(SD) = 0.02, and P(OD) = 0.08 
Required probability = P(G | ODc)

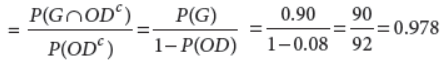
OR

If A and B are two independent events such that P (A∩B) = 2/15 and P (A∩B) = 1/6 , then find P (B) – P(A).
Answer : Since A and B are independent events, therefore, Ac and B are independent and also A and Bc are independent.
∴ P (A ∩ B) = P(Ac ∩ B) = P (Ac) P(B) = (1 – P(A)) P(B)
and P(A ∩ B ) = P(A ∩ B^c) = P(A) P (B^c)

24. Simplify : cos−1 (3/5 cosx+4/5 sinx)
Answer : 

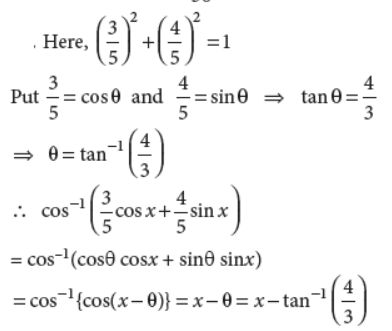
25. Find the points on the line x+2/3 = y+1/2 = z-3/2 at a distance of 5 units from the point P(1, 3, 3).
Answer : Any point on the line x+2/3 = y+1/2 = z-3/2 =λ(say) is
of the form Q(3λ – 2, 2λ – 1, 2λ + 3) …(i)
Now, distance PQ, where P is (1, 3, 3), is 5.
So, (3λ – 2 – 1)² + (2λ – 1– 3)² + (2λ + 3 – 3)2 = 52
⇒ 9λ² + 9 – 18λ + 4λ2 + 16 – 16λ + 4λ2 = 25
⇒ 17λ² – 34λ = 0 ⇒ 17λ(λ – 2) = 0
⇒ λ = 0 or λ = 2
Putting values of λ in (i), the required points are
(– 2, – 1, 3) and (4, 3, 7).

26. Find the solution of differential equation y³ – dy/dx = x² dy/dx.
Answer : 

27. If ā = -3î+nĵ+4k̂and Ђ = 2î+4ĵ+pk̂ are collinear, then find the value of n and p.
Answer : We have, ā and Ђ are collinear.

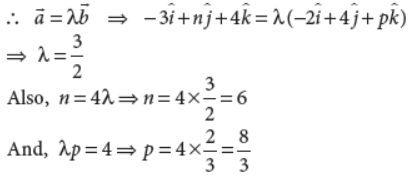
28. Find the equation of the tangent to the curve y = 3x² – x + 1 at P (1, 2).
Answer : y = 3x² – x + 1 is the given curve.
Differentiating w.r.t. x, we have

OR

Show, that the function f (x) = x⁹ + 4x⁷ + 11 is increasing on R.
Answer : Here, f(x) = x⁹ + 4x⁷ + 11
∴ f ′(x) = 9x⁸ + 28x⁶ = x6(9x² + 28) > 0 for all x ∈R
Thus, f(x) is increasing on R.

Section – IV

29. Show that f(x) = [x] is not differentiable at x = 1.
Answer : 

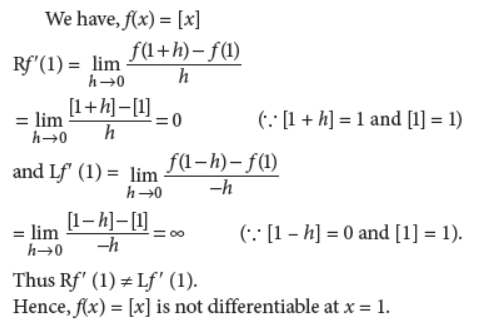
30. Find the area bounded by the X-axis, part of the curve y= 1+8/x2 and the ordinates at x = 2 and x = 4.
Answer : 

31. Find the equation of normal to the curve 16×2 + 9y2 = 144 at (2, y1) where y1 > 0.
Answer : 

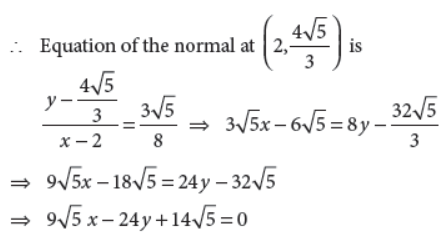
OR

Find the interval on which the function

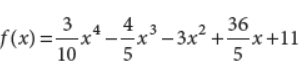
 is increasing
Answer : 

⇒ 6x³ – 12x² – 30x + 36 > 0
⇒ 6(x³ – 2x² – 5x + 6) > 0
⇒ 6(x – 1)(x – 3)(x + 2) > 0
The possible intervals are (–∞, –2), (–2, 1), (1, 3) and (3, ∞)
For f(x) to be increasing, f ′(x) > 0.
⇒ (x – 1) (x – 3) (x + 2) > 0
⇒ x ∈ (–2, 1) ∪ (3, ∞)

32. Solve the differential equation dy/dx + y cot x = 2cos x.
Answer : 

This is the required solution of the given differential equation.

33. Show that the relation R in the set A = {1, 2, 3, 4, 5, 6} given by R = {(a, b) : |a – b| is divisible by 2} is an equivalence relation.
Answer : We have, A = {1, 2, 3, 4, 5, 6} and R = {(a, b) : |a – b| is divisible by 2}
(i) Reflexive : For any a ∈ A
|a – a| = 0, which is divisible by 2.
Thus, (a, a) ∈ R. So, R is reflexive.

(ii) Symmetric : For any a, b ∈ A
Let (a, b) ∈ R
⇒ |a – b| is divisible by 2
⇒ |b – a| is divisible by 2
⇒ (b, a) ∈ R
∴ (a, b) ∈ R ⇒ (b, a) ∈ R
∴ R is symmetric.

(iii) Transitive : For any a, b, c ∈ A
Let (a, b) ∈ R and (b, c) ∈ R
⇒ |a – b| is divisible by 2 and |b – c| is divisible by 2.
⇒ a – b = ±2 k1 and b – c = ± 2k2; k1, k2 ∈ N
⇒ a – b + b – c = ±2(k1 + k2)
⇒ a – c = ±2 k3, k3 ∈ N
⇒ |a – c| is divisible by 2
⇒ (a, c) ∈ R
∴ R is transitive.
Hence, R is an equivalence relation.

34. Show that the exponential function ax is (where a > 0) continuous at every point.
Answer : 

∴ f is continuous at x = c, where c is an arbitrary real number.
∴ f (x) = ax is continuous at every point.

OR

Check whether the function

 is continuous or not.
Answer : 

35. Evaluate

Answer : 

36. An amount of ` 5000, is put into three investments at the rate of interest of 6%, 7% and 8% per annum respectively. The total annual income is ` 358. If the combined income from the first two investments is ` 70 more than the income from the third, find the amount of each investment by matrix method.
Answer : Let x, y and z be the investments at the rate of interest of 6%, 7% and 8% per annum respectively.
Then, x + y + z = 5000.
Income from investment of ₹ x, ₹ y and ₹ z is ₹6/100 ,7/100 and ₹8/100 respectively.

⇒ 6x + 7y – 8z = 7000
So, we obtain the following system of linear equations :
x + y + z = 5000
6x + 7y + 8z = 35800
6x + 7y – 8z = 7000
The system of equations can be written in matrix form as:

So, A^–1 exist and the solution of the given system of equations is given by X = A^–1 B.

x =1000, y = 2200, z = 1800
Hence, three investments are of ₹ 1000, ₹ 2200 and ₹ 1800 respectively.

OR

Express the following matrix as the sum of a symmetric matrix and a skew-symmetric matrix and verify your result :

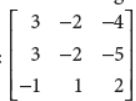
Answer : 

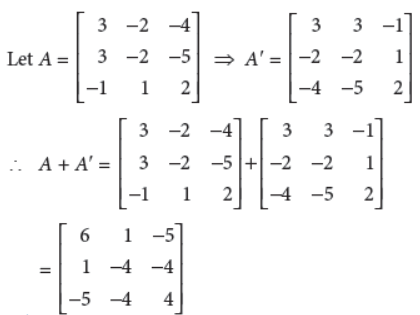
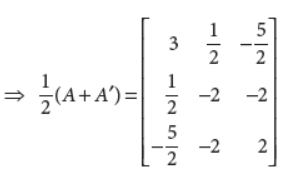
which is clearly a symmetric matrix and

Thus A has been expressed as the sum of a symmetric matrix and a skew-symmetric matrix.

37. Find the image of the point (1, – 2, 1) in the line x-2/3 = y+1/-1 =z+3/2
Answer : Let P(1, –2, 1) be the given point and let Q be the foot of the perpendicular drawn from P on of the given line

x-2/3 = y+1/-1 = z+3/2 = λ(say)
⇒ x = 3λ + 2, y = – λ – 1, z = 2λ – 3
λet the coordinates of Q be
(3λ + 2, – λ – 1, 2λ – 3) …(i)
So, direction ratios of PQ be
(3λ + 2 – 1, – λ – 1+ 2, 2λ – 3 – 1)
i.e., (3λ + 1, – λ + 1, 2λ – 4)
Since PQ is perpendicuλar to given λine.
∴ 3(3λ + 1) – 1(– λ + 1) + 2(2λ – 4) = 0
⇒ 9λ + 3 + λ – 1 + 4λ – 8 = 0 ⇒ λ = 3/7
Putting λ= 3/7 in (i), we get the coordinates of Q as

OR

The lines  r̄.(2ĵ-2k̂)+λ(mî +2ĵ+3k̂) and  r̄.(2î+6ĵ+3k̂)+μ(2î+3ĵ+4k̂)are coplanar. Find the value of m.
Answer : 

38. Find the maximum value of Z = 4x + 6y subject to constraints 3x + 2y ≤ 12, x + y ≥ 4, x ≥ 0, y ≥ 0.
Answer : Converting inequations into equations and drawing the corresponding lines.

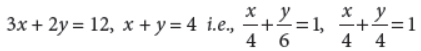
As x ≥ 0, y ≥ 0 solution lies in first quadrant.
We have points A(4, 0), B(0, 6) and C(0, 4).

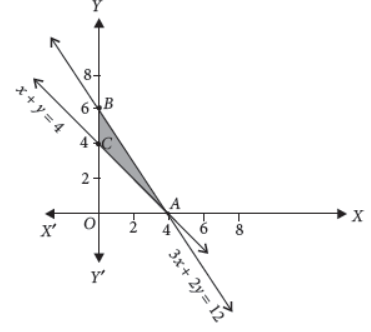
Now, Z = 4x + 6y
Z(A) = 4(4) + 6(0) = 16
Z(B) = 4(0) + 6(6) = 36
Z(C) = 4(0) + 6(4) = 24
∴Z has maximum value 36 at B(0, 6).

OR

Find the number of points at which he objective function Z = 4x + 3y can be maximized subject to the constraints 3x + 4y ≤ 24, 8x + 6y ≤ 48, x ≤ 5, y ≤ 6, x ≥ 0, y ≥ 0.
Answer : Converting inequations into equations and draw the corresponding lines
3x + 4y = 24, 8x + 6y = 48, x = 5, y = 6

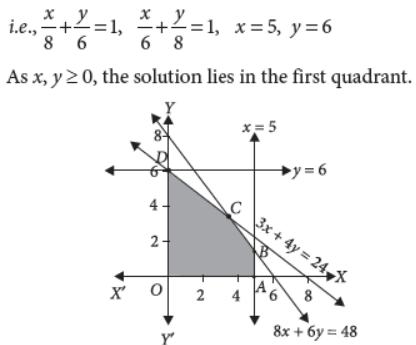
B is the point of intersection of the lines
8x + 6y = 48 and x = 5 i.e., B = (5,4/3)
C is the point of intersection of the lines 3x + 4y = 24
and 8x + 6y = 48 i.e. C =(24/7 , 24/7)
We have points O(0, 0) A(5, 0), B (5 , 4/3) , C(24/7 , 24/7) and D(0, 6).
Now, Z = 4x + 3y
\ Z(O) = 4(0) + 3(0) = 0
Z(A) = 4(5) + 3(0) = 20

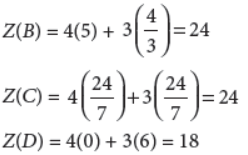
Z has maximum value at points B and C. Since both the points lie on the same line 8x + 6y = 48.
∴ Each point of the line 8x + 6y = 48 will give maximum value of Z. Therefore, objective function can be maximized at infinite number of points.