MCQs for Physics Class 11 with Answers Chapter 14 Oscillations
Students of class 11 Physics should refer to MCQ Questions Class 11 Physics Oscillations with answers provided here which is an important chapter in Class 11 Physics NCERT textbook. These MCQ for Class 11 Physics with Answers have been prepared based on the latest CBSE and NCERT syllabus and examination guidelines for Class 11 Physics. The following MCQs can help you to practice and get better marks in the upcoming class 11 Physics examination
Chapter 14 Oscillations MCQ with Answers Class 11 Physics
MCQ Questions Class 11 Physics Oscillations provided below have been prepared by expert teachers of grade 11. These objective questions with solutions are expected to come in the upcoming Standard 11 examinations. Learn the below provided MCQ questions to get better marks in examinations.
Question. The function sinwt – coswt represents
(a) a simple harmonic motion with a period π/ω.
(b) a simple harmonic motion with a period 2π/ω.
(c) a periodic, but not simple harmonic motion with a period π/ω.
(d) a periodic, but not simple harmonic motion with a period 2π/ω.
Answer
B
Question. A block of mass 200 g executing SHM under the influence of a spring of spring constant k = 90 N m–1 and a damping constant b = 40 g s–1. The time elapsed for its amplitude to drop to half of its initial value is
(Given ln (1/2) = –0.693)
(a) 7 s
(b) 9 s
(c) 4 s
(d) 11 s
Answer
A
Question. A particle executes SHM of type x = Asinwt. It takes time t1 from x = 0 to x = A/2 and t2 from x = A/2 to x = A. The ratio t1 : t2 will be
(a) 1 : 1
(b) 1 : 2
(c) 1 : 3
(d) 2 : 1
Answer
B
Question. Which of the following relationships betweenthe acceleration a and the displacement x of a particle involve simple harmonic motion?
(a) a = 0.7 x
(b) a = –200 x2
(c) a = –10 x
(d) a = 100 x3
Answer
C
Question. A spring balance has a scale that reads from 0 to 50 kg. The length of the scale is 20 cm. A block of mass m is suspended from this balance when displaced and released, it oscillates with a period 0.5 s. The value of m is (Take g = 10 m s–2)
(a) 8 kg
(b) 12 kg
(c) 16 kg
(d) 20 kg
Answer
C
Question. Four pendulums A, B, C and D are suspended from the same elastic support as shown in figure. A and C are of the same length, while B is smaller than A and D is larger than A.
If A is given a transverse displacement then
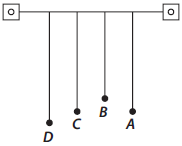
(a) D will vibrate with maximum amplitude
(b) C will vibrate with maximum amplitude
(c) B will vibrate with maximum amplitude
(d) all the four will oscillate with equal amplitude.
Answer
B
Question. A particle executes simple harmonic motion between x = – A and x = + A. The time taken for it to go from 0 to A/2 is T1 and to go from A/2 to A is T2. Then
(a) T1 < T2
(b) T1 > T2
(c) T1 = T2
(c) T1 = 2T2
Answer
A
Question. When the displacement of a particle executing SHM is one-fourth of its amplitude, what fraction of the total energy is the kinetic energy?
(a) 16/15
(b) 15/16
(c) 3/4
(d) 4/3
Answer
B
Question. An air chamber of volume V has a neck of cross-sectional area a into which a light ball of mass m just fits and can move up and down without friction. The diameter of the ball is equal to that of the neck of the chamber. The ball is pressed down a little and released.If the bulk modulus of air is B, the time period of the oscillation of the ball is
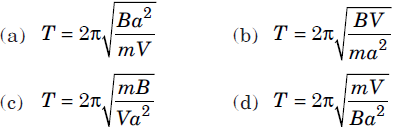
Answer
D
Question. The maximum speed of a particle executing S.H.M. is 10 m/s and maximum acceleration is 31.4 m/s2. Its periodic time is
(a) 2 s
(b) 4 s
(c) 6 s
(d) 1 s
Answer
A
Question. A trolley of mass 3 kg, as shown in figure, is connected to two identical springs, each of spring constant 600 N m–1. If the trolley is displaced from its equilibrium position by 5 cm and released, the maximum speed of the trolley is
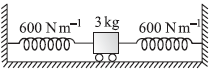
(a) 0.5 m s–1
(b) 1 m s–1
(c) 2 m s–1
(d) 3 m s–1
Answer
B
Question. A block whose mass is 1 kg is fastened to a spring. The spring has a spring constant of 100 N m–1. The block is pulled to a distance x = 10 cm from its equilibrium position at x = 0 on a frictionless surface from rest at t = 0. The kinetic energy and potential energy of the block when it is 5 cm away from the mean position is
(a) 0.375 J, 0.125 J
(b) 0.125 J, 0.375 J
(c) 0.125 J, 0.125 J
(d) 0.375 J, 0.375 J
Answer
A
Question. The x-t graph of a particle undergoing simple harmonic motion is shown in figure. The acceleration of the particle at t = 4/3 s is

Answer
D
Question. A particle executing SHM is described by the displacement function x(t) = Acos(ωt + ∅),If the initial (t = 0) position of the particle is 1 cm, its initial velocity is π cm s–1 and itsangular frequency is p s–1, then the amplitude of its motion is
(a) π cm
(b) 2 cm
(c) √2 cm
(d) 1 cm
Answer
C
Question. The length of a seconds pendulum on the surface of earth is 1 m. Its length on the surface of the moon is
(a) 1/6 m
(b) 1 m
(c) 1/36 m
(d) 36 m
Answer
A
Question. A simple pendulum executing SHM with a period of 6 s between two extreme positions B and C about a point O. If the length of the arc BC is 10 cm, how long will the pendulum take the move from position C to a position D towards O exactly midway between C and O?
(a) 0.5 s
(b) 1 s
(c) 1.5 s
(d) 3 s
Answer
B
Question. A U-tube of uniform cross-section holds 1 kg of pure mercury and 0.2 kg of water in equilibrium. The diameter of cross-section is 1.2 cm. Relative density of mercury is 13.6. If the system in equilibrium is slightly disturbed, the period of oscillation of the liquid column in the tube will be (take g = 10 m s–2)
(a) 0.1 s
(b) 1.5 s
(c) 0.50 s
(d) 0.2 s
Answer
D
Question. Starting from the origin, a body oscillates simple harmonically with a period of 2 s. After what time will its kinetic energy be 75% of the total energy ?
(a) 1/6 s
(b) 1/4 s
(c) 1/3s
(d) 1/12 s
Answer
A
Question. The amplitude of a damped oscillator becomes {1/3}rd in 2 seconds. If its amplitude after 6 seconds is 1/n times the original amplitude, the value of n is
(a) 32
(b) 3√3
(c) 23
(d) 33
Answer
D
Question. Displacement-time graph of a particle executing S.H.M. is shown below.
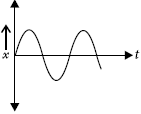
The corresponding force-time graph of the particle can be

Answer
D
Question. Consider a pair of identical pendulums, which oscillate with equal amplitude independently such that when one pendulum is at its extreme position making an angle of 2° to the right with the vertical, the other pendulum makes an angle of 1° to the left of the vertical. The phase difference between the pendulums is
(a) π/2
(b) 2/3 π
(c) 3/2 π
(d) π
Answer
B
Question. A simple pendulum has time period T1. The point of suspension is now moved upward according to the relation y = Kt2. (K = 1 m s–2) where y is the vertical displacement. The time period now becomes T2. The ratio of T21 / T22 (Take g = 10 m s–2)
(a) 6/5
(b) 5/6
(c) 1
(d) 4/5
Answer
A
Assertion & Reasoning Based MCQs :
two statements are given-one labelled Assertion (A) and the other labelled Reason (R) Select the correct answer to these questions from the codes (a), (b), (c) and (d) as given below.
(a) Both A and R are true and R is the correct explanation of A
(b) Both A and R are true but R is NOT the correct explanation of A
(c) A is true but R is false
(d) A is false and R is also false
Question. Assertion (A) : The percentage change in time period is 1.5%, if the length of simple pendulum increases by 3%.
Reason (R) : Time period is directly proportional to length of pendulum.
Answer
A
Question. Assertion (A) : Resonance is a special case of forced vibration in which the natural frequency of vibration of the body is the same as the impressed frequency and the amplitude of forced vibration, is maximum.
Reason (R) : The amplitude of forced vibrations of a body increases with an increase in the frequency of the externally impressed periodic force.
Answer
C
Question. Assertion (A) : Damped oscillation indicates loss of energy.
Reason (R) : The loss in damped oscillation may be due to friction, air resistance etc.
Answer
A
Question. Assertion (A) : When a simple pendulum is made to oscillate on the surface of moon, its time period increases.
Reason (R) : Moon is much smaller as compared to earth.
Answer
B
Question. Assertion (A) : The value of acceleration due to gravity is low at the mountain top than at the plane.
Reason (R) : If a pendulum clock is taken to mountain top, it will gain time.
Answer
C
Question. Assertion (A) : The bob of a simple pendulum is a ball full of water. If a fine hole is made at the bottom of the ball, then the time period will no more remain constant.
Reason (R) : The time period of a simple pendulum does not depend upon mass.
Answer
B
Question. Assertion (A) : If a man with a wrist watch on his hand falls from the top of a tower, its watch gives correct time during the free fall.
Reason (R) : The working of the wrist watch depends on spring action and it has nothing to do with gravity.
Answer
A
Question. Assertion (A) : Simple harmonic motion is not a uniformly accelerated motion.
Reason (R) : Velocity is non uniform in SHM.
Answer
B
Question. Assertion (A) : The frequency of a second pendulum in an elevator moving up with an acceleration half the acceleration due to gravity is 0.612 s–1.
Reason (R) : The frequency of a second pendulum does not depend upon acceleration due to gravity.
Answer
C
Question. Assertion (A) : In real situation the amplitude of forced oscillation can never be infinite.
Reason (R) : The energy of oscillator is continuously dissipated.
Answer
B
Case Based MCQs :
Simple Harmonic Motion
Simple harmonic motion is the simplest form of oscillation. A particular type of periodic motion in which a particle moves to and fro repeatedly about a mean position under the influence of a restoring force is termed as simple harmonic motion (S.H.M).
A body is undergoing simple harmonic motion if it has an acceleration which is directed towards a fixed point, and proportional to the displacement of the body from that point.
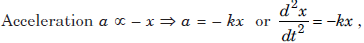
where x = displacement at any instant t.
Question. Which of the following is not a characteristics of simple harmonic motion?
(a) The motion is periodic.
(b) The motion is along a straight line about the mean position.
(c) The oscillations are responsible for the energy conversion.
(d) The acceleration of the particle is directed towards the extreme position.
Answer
D
Question. Which of the following motions is not simple harmonic?
(a) Vertical oscillations of a spring
(b) Motion of a simple pendulum
(c) Motion of planet around the Sun
(d) Oscillation of liquid in a U-tube
Answer
C
Question. Which of the following expressions does not represent simple harmonic motion?
(a) x = Acosωt + Bsinωt
(b) x = Acos(ωt + a)
(c) x = Bsin(ωt + b)
(d) x = Asinωt cos2ωt
Answer
D
Question. The equation of motion of a simple harmonic motion is

Answer
A
Question. The time period of simple harmonic motion depends upon
(a) amplitude
(b) energy
(c) phase constant
(d) mass
Answer
D
Damped Simple Harmonic Motion
The oscillations in presence of dissipative force where the amplitude decreases gradually with the passage of time are called damped oscillations. A part of the energy of the oscillating system is lost in the form of heat, in overcoming these resistive forces, As a result, the amplitude of such oscillations decreases exponentially with time, as shown in figure. Eventually, these oscillations die out. In these oscillations, the amplitude of oscillation decreases exponentially due to damping forces like frictional force, viscous force, etc. Due to decrease in amplitude, the energy of the oscillator also goes on decreasing exponentially.
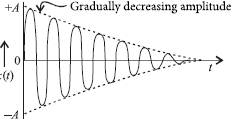
The force producing a resistance to the oscillation is called damping force.
Question. Which of the following displacement-time graphs represent damped harmonic oscillation?
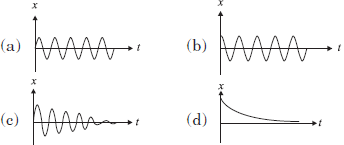
Answer
C
Question. The S.I. unit of damping constant is
(a) kg s
(b) kg2s
(c) kg m/s
(d) kg/s
Answer
D
Question. In case of a force vibration, the resonance wave becomes very sharp when the
(a) applied periodic force is small
(b) damping force is small
(c) quality factor is small
(d) restoring force is small
Answer
B
Question. A particle oscillating under a force

is a (k and b are constants)
(a) simple harmonic oscillator
(b) linear oscillator
(c) damped oscillator
(d) forced oscillator
Answer
C

