Sample Paper Class 12 Mathematics Set B
PART – A
Section – I
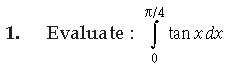
(a) 1
(b) 2
(c) log 2
(d) (1/2)log 2
Answer
D
2. Find the integrating factor of the differential equation
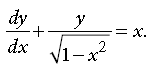

Answer
A
3. Find the unit vector in the direction of vector a̅, = 2î + 3ĵ + 4k̂
(a) (2î + 3ĵ + 9k̂)√29
(b) 2î + 3ĵ + 9k̂
(c) −(2î + 3ĵ + 9k̂)√29
(d) (2î + 3ĵ + 9k̂)√25
Answer
A
4. Two dice are thrown together. What is the probability that the sum of the numbers on the two faces is neither 9 nor 11 ?
(a) 1/6
(b) 5/6
(c) 2/3
(d) 1/3
Answer
B
Section – II
Case study-based question is compulsory. Attempt any 4 sub parts. Each sub-part carries 1 mark.
5. Ishaan left from his village on weekend. First, he travelled up to temple. After this, he left for the zoo. After this he left for shopping in a mall. The positions of Ishaan at different places is given in the following graph.

Based on the above information, answer the following questions.
(i) Position vector of B is
(a) 3î + 5ĵ
(b) 5î + 3ĵ
(c) −5î − 3ĵ
(d) −5î + 3ĵ
Answer
B
(ii) Position vector of D is
(a) 5î + 3ĵ
(b) 3î + 5ĵ
(c) 8î + 9ĵ
(d) 9î + 8ĵ
Answer
D
(iii) Find the vector
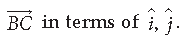
(a) î − 2ĵ
(b) î + 2ĵ
(c) 2î + ĵ
(d) 2î − ĵ
Answer
B
(iv) Length of vector
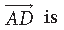
(a) √67 units
(b) √85 units
(c) √90 units
(d) √100 units
Answer
B
(v) If M̅ = 4ĵ + 3k̂, then its unit vector is

Answer
A
PART – B
Section – III

Answer.

7. Prove that the area bounded by the parabola y2 = 4ax and the line x = a and x = 4a is

Answer. Required area = 2 × area of region PSRQP
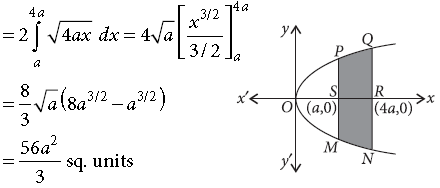
8. Find the distance from the origin to the plane x + 3y – 2z + 1 = 0.
Answer. Required distance,

9. Find order and degree of the equation

Answer.

10. Find the value of î (ĵ x k̂) + ĵ (î x k̂) + (î x 3ĵ)
Answer. î ⋅ î + ĵ (- ĵ ) + k̂ ⋅ k̂ = 1 – 1 + = 1
Section – IV
11. A bag contains 12 white pearls and 18 black pearls. Two pearls are drawn in succession without replacement. Find the probability that the first pearl is white and the second is black.
Answer. Let A and B be the events of getting a white pearl in the first draw and a black pearl in the second draw respectively.
Now, P(A) = P(getting a white pearl in the first draw)
When second pearl is drawn without replacement, the probability that the second pearl is black is the conditional probability of the event B occurring when A has already occurred.

12. Find the direction cosines of the line passing through the two points (–2, 4, –5) and (1, 2, 3).
Answer. We know that the direction cosines of the line passing through two points P(x1, y1, z1) and Q(x2, y2, z2) are given by
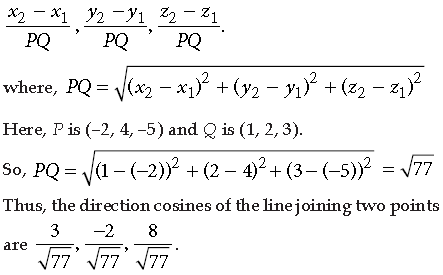

Answer.

14. A machine produces parts that are either good (90%), slightly defective (2%), or obviously defective (8%). Produced parts get passed through an automatic inspection machine, which is able to detect any part that is obviously defective and discard it. What is the probability of the parts that make it through the inspection machine and get shipped?
Answer. Let G, SD, OD be the events that a randomly chosen part is good, slightly defective, obviously defective respectively.
Then, P(G) = 0.90, P(SD) = 0.02, and P(OD) = 0.08
Required probability = P(G | ODc)

Section – V
15. If A and B are two independent events such that P (A̅∩B) = 2/15 and P (A∩B̅) = 1/6, then find P (B) – P(A).

Answer. Since A and B are independent events, therefore, Ac and B are independent and also A and Bc are independent.
∴ P(Ac ∩ B) = P (Ac) P(B) = (1 – P(A)) P(B)
and P(A ∩ Bc) = P(A) P (Bc)
= P (A) (1 – P(B)) ( A = Ac and B = Bc)


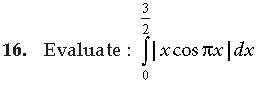
Answer.


Answer.


Section – VI
18. Find the equation of the plane passing through the point A(1, 2, 1) and perpendicular to the line joining the points P(1, 4, 2) and Q(2, 3, 5). Also, find the distance of this plane from the line
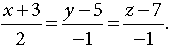
OR
Find the coordinates of the points on the line
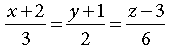
which are at a distance of 2 units from the point (–2, –1, 3).
Answer. The line joining the given points
P(1, 4, 2) and Q(2, 3, 5) has direction ratios
<1 – 2, 4 – 3, 2 – 5> i.e., <– 1, 1, –3>
The plane through (1, 2, 1) and perpendicular to the
line PQ is –1(x – 1) + 1(y – 2) – 3(z – 1) = 0
⇒ x – y + 3z – 2 = 0

Since 2(1) + (–1) (–1) + (3) (–1) = 2 + 1 – 3 = 0
∴ Line is parallel to the plane.
Since, (–3, 5, 7) lies on the given line.
∴ Distance of the point (–3, 5, 7) from plane is


19. Find the area of the smaller region bounded by the ellipse

OR
Draw the graph of y = |x + 1|and using integration, find the area below y = |x + 1|, above x – axis
and between x = – 4 to x = 2.
Answer.

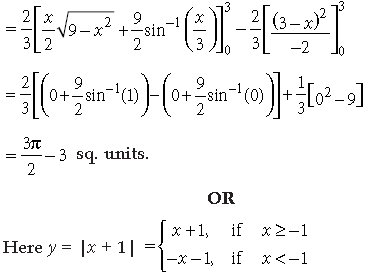
Thus we get two lines –x + y = 1 …(i), x + y = –1 …(ii)
Their graphs are as shown and the area to be calculated is shaded.

