Sample Paper Class 12 Mathematics Term 1 Set B
1. Evaluate (57 – 42)mod 11.
(a) 3
(b) 5
(c) 9
(d) 4
Answer
D
2. The remainder when 2100 is divided by 5 is
(a) 1
(b) 2
(c) 3
(d) 4
Answer
A

Answer
B
4. If A2 + A + I = O , then A-1 is equal to
(a) A- I
(b) I – A
(c) – (A+ I)
(d) None of these
Answer
C

Answer
B
6. The equation of normal at (1, 2) to the curve y x 2 = 4 is
(a) 4x – y = 2
(b) x + y – 3 = 0
(c) y – x = 1
(d) None of these
Answer
B
7. The function f (x) = log x is _________ on its domain .
(a) increasing
(b) decreasing
(c) Both (a) and (b)
(d) None of these
Answer
A
8. If the cost function of a firm is given by C(x) = 2x – 4x + 5 2 , then average cost, when x = 2 is
(a) 2.5
(b) 2
(c) 1.5
(d) 1
Answer
A
9. The index number for the base year is
(a) 95
(b) 100
(c) 110
(d) 120
Answer
B
10. Price index by Marshall Edgeworth’s method considered
(a) only base year quantity.
(b) only base year prices.
(c) only current year prices and quantity.
(d) Both the current year as well as base year prices and quantities
Answer
D
11. Given that, ∑p0q0 = 246, ∑p0q1 = 208, ∑p1q0 = 2.12 and p1q1 = 295, where subscript 0 and 1 are used for base year and current year respectively. The Paasche’s index number is
(a) 141.83
(b) 162.24
(c) 143.14
(d) 164.12
Answer
A
12. An urn contains 6 red and 3 black balls. Two balls are randomly drawn. Let X represents the number of black balls. The possible values of X are
(a) 0, 1, 3
(b) 0, 1
(c) 1, 2, 3
(d) 0, 1, 2
Answer
D
13. For the following probability distribution.

E(X) is equal to
(a) 0
(b) – 1
(c) – 2
(d) – 1.8
Answer
D
14. Let X is a normal distribution random variable with mean m = 55 and standard deviation s = 12. The value of probability P(X < 70) is [given, F (1.25) = 0.8944]
(a) 0.9332
(b) 0.9216
(c) 0.8944
(d) 0.1056
Answer
C
15. If l = 1 in Poisson distribution, then the value of P(5) is
(a) 0.307
(b) 0.00307
(c) 0.0307
(d) 0.000307
Answer
B

Answer
A
17. The area of the triangle with vertices (- 1, 2), (4, 0) and (3, 9) is k sq units, then k is
(a) 43
(b) 43/2
(c) 20
(d) 43/3
Answer
B

Answer
D
19. A, B and C are three contestants is 800 m race. If A can give B a start of 20 m and A can given C a start of 32 m, then B gives C a start of
(a) 12.310 m
(b) 11.307 m
(c) 13.307 m
(d) 12.703 m
Answer
A
20. Aman can row with a speed of 8 km/h in still water. If the speed of stream is 4 km/h, then the upstream speed of boat is
(a) 4 km/h
(b) 6 km/h
(c) 5 km/h
(d) 12 km/h
Answer
A
Section B
21. The unit’s digit in 6600 is
(a) 2
(b) 4
(c) 6
(d) 8
Answer
C
22. The last three-digits of the product 2345 X 4567 is
(a) 615
(b) 515
(c) 415
(d) 325
Answer
A

(a) y = 2x
(b) y = – 2x
(c) y = x
(d) y = – x
Answer
A

Answer
B
25. The function f (x) xx = has a stationary point at
(a) x = e
(b) x = 1/e
(c) x = 1
(d) x = e
Answer
B
26. The interval on which the function f (x) = 2x3 + 9x2 + 12x – 1 is decreasing is
(a) [- 1, ∞)
(b) [- 2, – 1]
(c) (- ∞, – 2]
(d) [- 1, 1]
Answer
B
27. For the given data ∑p1q1 = 300, ∑p0 q0 = 250, ∑p1q0 = 260 and ∑p0q1 = 280, where subscript 0 and 1 are used for base year and current year respectively. The Laspeyre’s price index is
(a) 160
(b) 120
(c) 130
(d) 135
Answer
B
28. Time reversal test determine whether a gives method will work
(a) in only backward way
(b) both ways in time, forward and backward
(c) in only forward way
(d) both ways in time and satisfied relation P01 X P10 = 2
Answer
B
29. By using relative prices, index number for the year 2015 with 2010 as base was 130 and
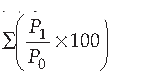
=450 5 and N = 4, then value of x is
(a) 20
(b) 14
(c) 16
(d) 18
Answer
B
30. Which of the following is the limitation of simple aggregative index?
(a) The units in which prices of commodities are given affect the price index
(b) The index is not influenced by the units in which prices are quoted
(c) Extreme items do not influence the index
(d) None of the above
Answer
A
31. Given that ∑ p1q1 = 136, ∑p0 q1 = 112, ∑p1q0 = 115 and ∑p0 q0 = 102, where subscript 0 and 1 are used for base year and current year resepctively. The Bowley’s index number is
(a) 1.17
(b) 1.46
(c) 1.73
(d) 1.09
Answer
A
32. Let X be a discrete random variable whose probability distribution is defined as follows

where, k is a constant. The value of k is
(a) 1/20
(b) 1/50
(c) 1/55
(d) 1/70
Answer
B
33. From a lot 30 bulbs, which includes 6 defective, 3 bulbs are drawn one-by-one at random with replacement. Using the probability distribution of number of defective bulbs. The mean of the distribution will be
(a) 1/5
(b) 2/5
(c) 3/5
(d) 4/5
Answer
B
34. A radar unit is used to measure speeds of cars on a motorway. The speeds are normally distributed with 76 km/h and a standard deviation of 16 km/h. The probability that a car picked at random is travelling at more than 100 km/h is [given, F(1.5) = 0.9332]
(a) 0.668
(b) 0.993
(c) 0.9332
(d) 0.0668
Answer
D
35. If the probability that an individual suffers a bad reaction from injection of a given serum is 0.002, then the probability that out of 1000 individuals exactly 2 individuals will suffer from a bad reaction is (use e-2 = 01353 .)
(a) 0.7936
(b) 0.7206
(c) 0.2706
(d) 0.2936
Answer
C
36. For the system of equations x + 3z = 9, x – 2y + 2z = -4 and 2x – 3y + 4z = -3, the value of x, y and z are respectively
(a) 0, 5 and 3
(b) 5, 0 and 3
(c) 0, 3 and 5
(d) 3, 0 and 5
Answer
A
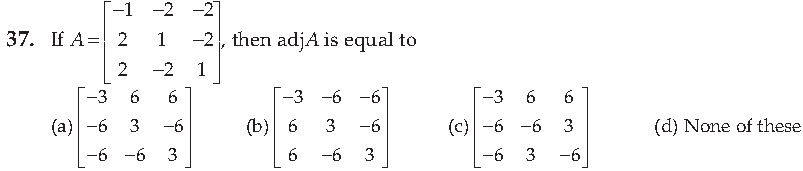
Answer
A
38. Roopal and Shanu invested in a business. Roopal invested ₹15000 for 4 months, while Shanu invested ₹10000 for 3 months. Out of the total profit of ₹ 90000. Roopal’s share in the investment is
(a) ₹35000
(b) ₹75000
(c) ₹ 55000
(d) ₹60000
Answer
D
39. A solution containing 15% spirit should be mixed with a solution containing 25% spirit, such that the resultant mixture contains 21% spirit in the ratio
(a) 1 : 3
(b) 2 : 3
(c) 3 : 4
(d) 4 : 5
Answer
B

(a) (1, 1)
(b) (1, -1)
(c) (-1, 1)
(d) (-1, -1)
Answer
C
Section C
41. 2 defective bulbs are mixed up with 7 good ones. 2 bulbs are drawn at random. In the probability distribution of defective bulbs, the term with minimum probability is
(a) 1/24
(b) 1/36
(c) 7/18
(d) 7/12
Answer
A
42. In a certain factory turning razor blades, there is a small chance 1/200 for any blade to be defective. The blades are in packets of 4. The approximate number of packets containing no defective blade in a consignment of 30000 packets is (use e-0 02 = 0 9802 . . )
(a) 28406
(b) 28506
(c) 29506
(d) 29406
Answer
D
43. The equation of the tangent to the curve

at the point, where it cuts X-axis, is
(a) 20x + y -140 = 0
(b) x -20y -7 = 0
(c) 20x – y +140 = 0
(d) x +20y +7 = 0
Answer
B
44. The speed of motorboat in still water is 45 km/h. If the motorboat travels 80 km along the stream in 1 h 20 min, then the time taken by it to cover the same distance against the stream will be
(a) 1 h 20 min
(b) 3 h 40 min
(c) 2 h 40 min
(d) 2 h 55 min
Answer
C
45. A mixture contains milk and water in the ratio 2 : 3. A certain quantity of milk is added to the mixture such that the ratio of milk and water becomes 2 : 1. The percentage of milk added in the original mixture with respect to original quantity of solution is
(a) 75%
(b) 60%
(c) 80%
(d) 50%
Answer
C
Case Study
A cistern has three pipes A, Band C. Pipe A and Bcan fill it in 5 h and 10 h respectively, while
pipe C can empty the cistern in 30 h.
Based on the above information, answer the following questions.
46. If the pipe A and B are opened, then the time taken to fill the cistern is
(a) 3 h 20 min
(b) 3 h
(c) 3 h 10 min
(d) 2 h 50 min
Answer
A
47. If all the pipes are opened, the time taken to fill the cistern is

Answer
B
48. If the pipe A and B are opened alternatively and pipe C is opened all the time, then the time taken to fill the cistern is
(a) 8 h 12 min
(b) 8 h 24 min
(c) 4 h 12 min
(d) 4 h 24 min
Answer
B
49. When the cistern is empty, tap A is opened at 7:00 am and tap B is opened at 10:00 am.
Both the taps are closed at 11:00 am. Tap C is opened at 3:00 pm, then the cistern will be empty at
(a) 6:00 pm (same day)
(b) 7:00 pm (same day)
(c) 6:00 pm (next day)
(d) 7:00 pm (next day)
Answer
C
50. If the tap A is opened partially in such a way that its efficiency of filling the cistern becomes half, then the time taken by all the three taps to fill the tank is
(a) 5 h
(b) 5 h 30 min
(c) 6 h
(d) 5 h 45 min
Answer
C
