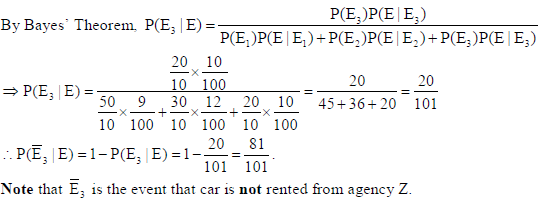Sample Paper Class 12 Mathematics Set J
SECTION A
1. If A and B are invertible matrices of order 3, |A| = 2 and |(AB)–1| = –1/6, find |B|.
Sol.
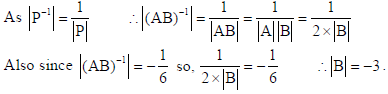
2. Differentiate sin2 (x2) w. r. t. x2.
Sol.
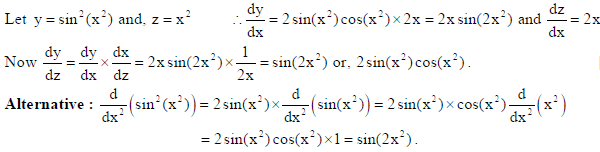
3. Write the order of the differential equation :
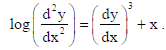
Sol.

4. Find the acute angle which the line with direction cosines 1/√3 , 1/√6 n makes with positive direction of z-axis.
Sol.
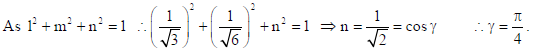
Here γ is the acute angle made by the line with positive direction of z-axis.
OR
Find the direction cosines of the line
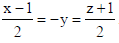
Sol. On Rewriting the line in Symmetrical form :

So, the d.r’s of the line are 2, –1, 2.
Hence the d.c.’s of the line are

SECTION B
5. Let A = Z × Z and * be a binary operation on A defined by (a, b) * (c, d) = (ad + bc, bd). Find the identity element for * in the set A.
Sol. Let (e, f ) ∈ A = Z × Z be the identity element for .
So, (a, b)*(e, f ) = (a, b) = (e,f )*(a,b) ∀ (a, b) ∈ A
i.e., if (af + be, bf ) = (a, b) = (eb + fa,fb)
Consider (af + be, bf ) = (a, b) and (a, b) = (eb + fa,fb)
i.e., af + be = a, bf = b and a = eb + fa, b = fb
i.e., a×1+ be = a,f =1 and a = eb +1×a,1 = f (if b ∈ Z − 0, i.e., b ≠ 0)
i.e., e = 0,f =1 and 0 = e,1 = f .
Hence (0, 1) is the identity element.
6.
Sol.
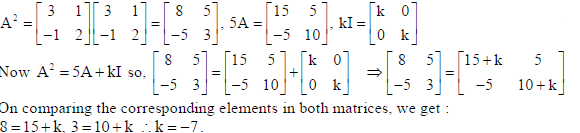
7.

Sol.
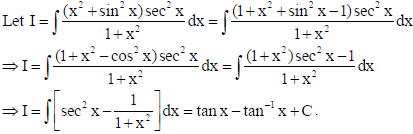
8.
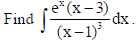
Sol.
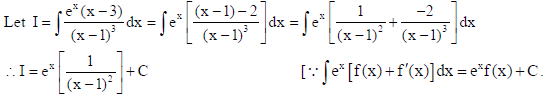
OR
Find
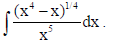
Sol.

9. Form the differential equation of all circles which touch the x-axis at the origin.
Sol. Let r be the radius of all circles which touch the x-axis at origin. So, centre of all such circles must lie on y-axis. Therefore, the centre will be of the form (0, r).
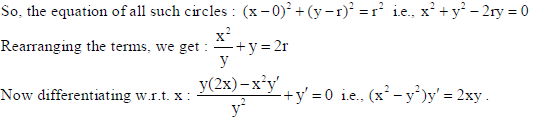
10. Find the area of the parallelogram whose diagonals are represented by the vectors
a̅ = 2 î −3ĵ+ 4k̂ and b̅ = 2 î − ĵ+ 2k̂.
Sol.
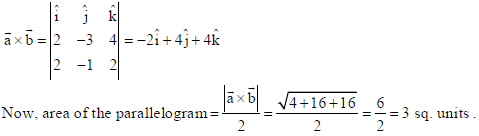
OR
Find the angle between the vectors a = î + ĵ− k̂ and b = î − ĵ+ k̂.
Sol. Let θ be the required angle between given vectors
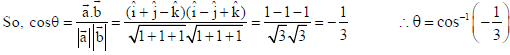
11. If A and B are two independent events, prove that A’ and B are also independent.
Sol. P(A’∩ B) = P(B−A) = P(B) − P(A∩B) = P(B) − P(A)P(B)
[∵ P(A ∩ B) = P(A)P(B), if A and B are independent events .
⇒ P(A’∩ B) = P(B)[1− P(A)] ∴ P(A’∩B) = P(A’)P(B)
Hence, A’ and B are also independent if A and B are independent events.
12. One bag contains 3 red and 5 black balls. Another bag contains 6 red and 4 black balls. A ball is transferred from first bag to the second bag and then a ball is drawn from the second bag. Find the probability that the ball drawn is red.
Sol. P(Red transferred and red drawn or black transferred and red drawn) = 3/8 × 7/11 + 5/8 × 6/11 = 51/88.
alternative : Let E : the ball drawn from second bag is red, E1 : red ball is transferred from first bag and E2 : black ball is transferred from first bag.
∴ P(E1) = 3/8, P(E2) = 5/8, P(E | E1 ) = 7/11, P(E | E2) = 6/11
So, P(E) = P(E1)P(E | E1) + P(E2)P(E | E2) = 3/8 × 7/11 + 5/8 × 6/11 = 51/88.
OR
If P(A) = 0.6, P(B) = 0.5 and P(A|B) = 0.3, then find P(A ∪ B).
Sol.

SECTION C
13. Prove that the function f :[0,∞)→R given by f (x) = 9x2 + 6x −5 is not invertible. Modify the codomain of the function f to make it invertible, and hence find f–1.
Sol. First of all, let’s check the function f (x) for one-one.

OR
Check whether the relation R in the set R of real numbers, defined by
R = {(a, b) :1+ ab > 0}, is reflexive, symmetric or transitive.
Sol. We have R = {(a, b) :1+ ab > 0}, where a, b ∈ R.
Reflexivity : Since 1+ aa =1+ a2 > 0 ∀ a ∈ R. So, (a, a) ∈ R. Hence, R is reflexive.
Symmetry : Let a, b ∈ R and (a, b) ∈ R.
Clearly 1+ ab > 0 implies, 1+ ba > 0 which further implies (b,a) ∈ R .
Hence R is symmetric.
Transitivity : Let a, b,c ∈ R and (a, b), (b, c) ∈ R.
Let a = −8, b = −1, c = 1/2
As 1+ ab =1+ (−8)(−1) = 9 > 0 ∴ (a,b) ∈ R and, 1 + bc = 1 + (−1)(1/2) = 1/2 > 0 ∴ (b,c) ∈ R
But, 1 + ac = 1 + (−8)(1/2) = −3 > 0, which is false. ∴(a,c) ∉ R.
Hence R isn’t transitive.
14.
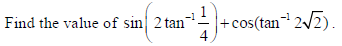
Sol.

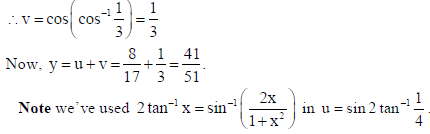
15. Using the properties of determinants, prove that
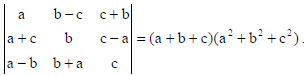
Sol.
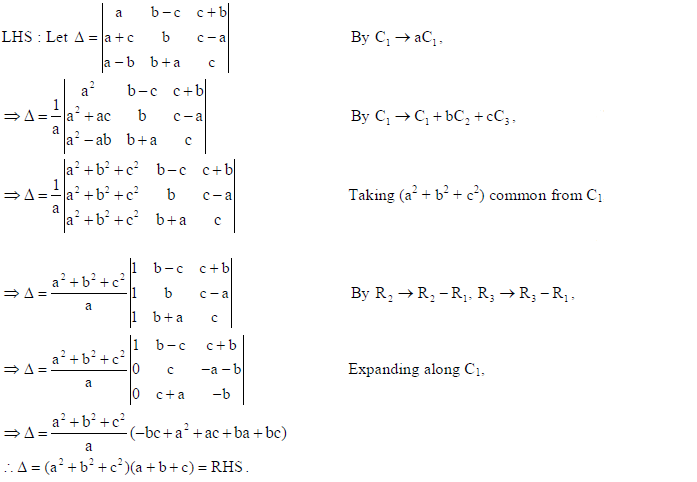
16. If y xsin x + sin(xx), find dy/dx.
Sol.

OR
If y = log(1 + 2t2 + t4 ), x = tan−1t, find d2y/dx2.
Sol.

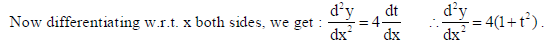
17.
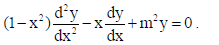
Sol.
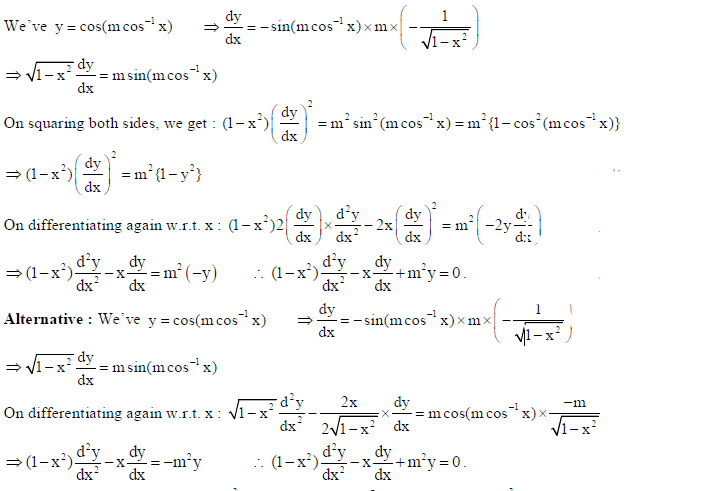
18. Find the equations of the normal to the curve y = 4x3 −3x + 5 which are perpendicular to the line 9x − y + 5 = 0 .
Sol. Let the normal to the curve y = 4x3 −3x + 5 be at P(α,β ). ∴β = 4α3 − 3α + 5…(i)
Now dy/dx = 12x2 −3 ∴ mN = −1/12α2 − 3 = Slope of normal at P(α,β)
As slope of the given line 9x − y + 5 = 0 is 9 and this line is perpendicular to the normal so,
(1/12α2 − 3) × 9 = − 1 i.e., 12α2 −3 = 9 ⇒ α2 =1 ∴ α = ±1, β = 6, 4 {By (i)
Therefore the points are (1, 6), (–1, 4).
Equations of Normals are : y − 6= −1/9 (x−1) i.e., x + 9y = 55 and,
y − 4= −1/9 (x+1) i.e., x + 9y = 35.
19. Find
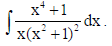
Sol.

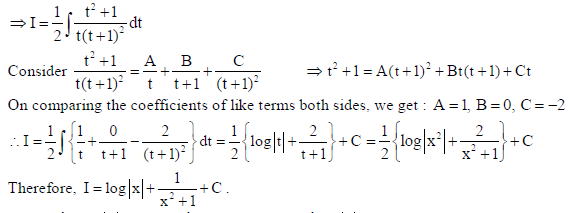
20. Evaluate
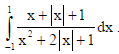
Sol.
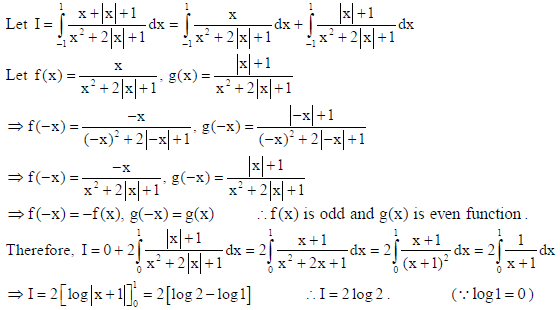
21. Find the particular solution of the following differential equation :
cos ydx (1+ 2e −x )sin ydy = 0; y(0) = π/4
Sol.
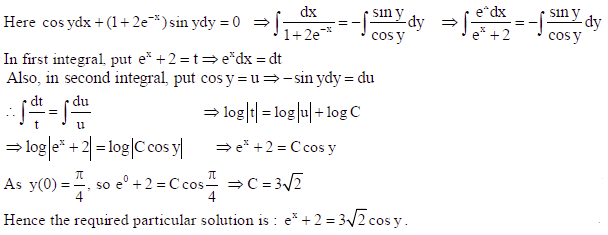
OR
Find the general solution of the differential equation :
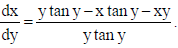
Sol.

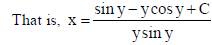
22. If p̅ = î + ĵ+ k̂ and q̅ = î − 2ĵ+ k̂ , find a vector of magnitude 5√3 units perpendicular to the vector q̅ and coplanar with vectors p̅ and q̅ .
Sol.

23. Find the vector equation of the line joining (1, 2, 3) and (–3, 4, 3) and show that it is perpendicular to the z-axis.
Sol. ∵ Vector eq. of the line joining two points with position vectors a̅ and b̅ is r̅ = a + λ(b̅ − a̅)
So, r̅ = î + 2ĵ+ 3k̂ + λ{(−3î + 4ĵ+ 3k̂ ) − (î + 2ĵ+ 3k̂)} i.e., r̅ = î + 2ĵ+ 3k̂ + λ(−4î + 2ĵ) …(i)
Now the d.r.’s of line (i) are –4, 2, 0. Also the d.r.’s of z-axis are 0, 0, 1.
Since (−4)(0) + (2)(0) + (0)(1) = 0 so, clearly line (i) is perpendicular to the z-axis.
(By using a1a2 +b1b2 + c1c2 = 0 , condition for perpendicular lines).
SECTION D
24.
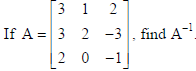
Hence, solve the system of equations : 3x + 3y + 2z =1, x + 2y = 4, 2x −3y − z = 5.
Sol.

OR
Find the inverse of the following matrix using elementary transformations :

Sol.

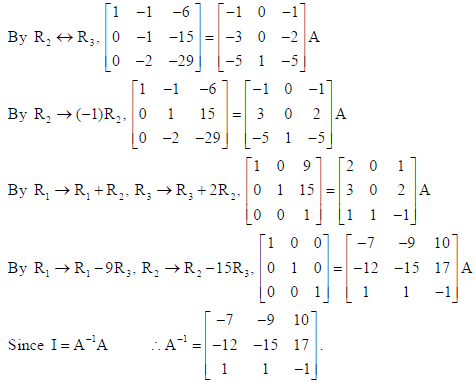
25. A cuboidal shaped godown with square base is to be constructed. Three times as much cost per square meter is incurred for constructing the roof as compared to the walls. Find the dimensions of the godown if it is to enclose a given volume and minimize the cost of constructing the roof and walls
Sol. Let the length and breadth of the base be x and the height of the godown be y.
Let C be the cost of constructing the godown and V be the given volume.

26. Find the area bounded by the curves y = √x, 2y + 3 = x and x-axis.
Sol.
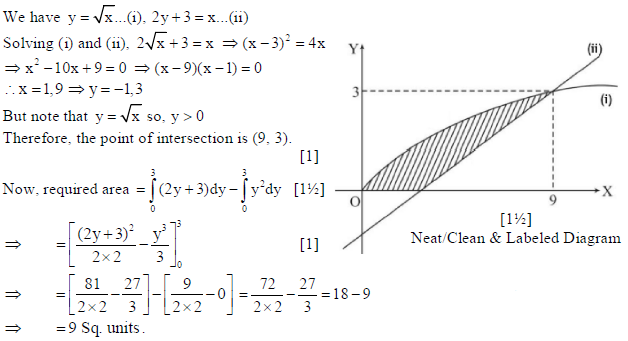
OR
Find the area of the region {(x, y) : x2 + y2 ≤ 8, x2 ≤ 2y}.
Sol.
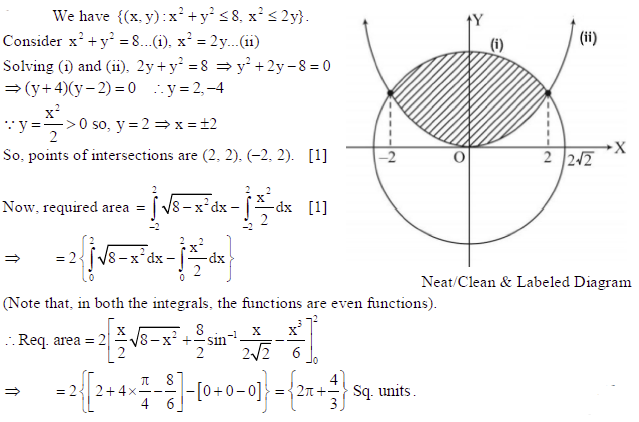
27.
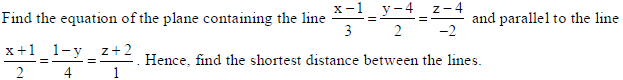
Sol.
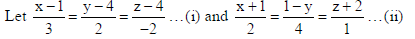
The d.r.’s of lines (i) and (ii) are respectively, 3, 2, –2; 2, –4, 1.
Let A, B, C be the d.r.’s of the Normal to the plane containing line (i). So, the required plane will surely contain the point (1, 4, 4), which is a point on line (i).
∴ π : A(x −1) + B(y − 4) + C(z − 4) = 0…(iii)
Since the line (i) is on the plane (iii) so, the normal to the plane will also be perpendicular to the line (i).
∴ 3A+ 2B− 2C = 0…(iv)
Also, line (ii) is parallel to the plane (iii) so, Normal to the plane will be perpendicular to the line (ii).
∴ 2A − 4B+1C = 0…(v)
By 2 × (iv) + (v), we get : A = 3C/8. Also 4B = 2A + C = 3C/4 + C = 7C/4 i.e., B = 7C/16
So, the d.r.’s of normal are A, B, C i.e., 3C/8 , 7C/16 , C i.e., 6, 7, 16
By (iii), the req. plane is π: 6(x −1) + 7(y − 4) +16(z − 4) = 0 i.e., 6x + 7y +16z −98 = 0.
Note that on the line (ii), a point is (–1, 1, –2).
Since the line (i) lies on the plane (iii) and (ii) is parallel to this plane so, the shortest distance between lines (i) and (ii) will be same as the distance of point (–1, 1, –2) from the plane.
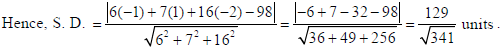
OR
Show that the line of intersection of the planes x + 2y + 3z = 8 and 2x + 3y + 4z =11 is
coplanar with the line
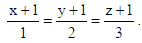
Also find the equation of the plane containing them.
Sol. Let π1 : x + 2y + 3z = 8 and π1 : 2x + 3y + 4z =11.
Let’s first of all, find a point which satisfies both these planes. This point will lie on the line of intersection of these two planes.
Consider x + 2y = 8 − 3z…(i), 2x + 3y =11− 4z…(ii)
By 2×(i) − (ii), we get : y = 5− 2z ∴x = z − 2
That is the required point is (x, y, z) i.e., (z − 2, 5 − 2z, z) ∴(−2, 5, 0)
(Note that, we have put z = 0. You can put any value of z in order to obtain the desired point).
Let P(–2, 5, 0). As this point satisfies both the planes so, it must lie on the line of intersection of these planes. Also the d.r.’s of normals to the planes (i) and (ii) are respectively 1, 2, 3; 2, 3, 4.

⇒ = −1 × 8 − 6×(−2) +1×(−4) = 0 = RHS.
So, the line of intersection of planes (i) and (ii) (i.e., the line (iii)) is coplanar with the line (iv).
Now for the equation of plane containing lines (iii) and (iv), let’s find the normal vector to the required plane.
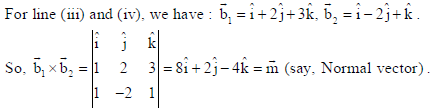
Also a point on the required plane may be taken from any one of the lines (iii) or, (iv). Let’s take a point from line (iii). Clearly (–2, 5, 0) i.e., a̅ = −2î + 5ĵ will lie on the required plane too. Now required eq. of plane : r̅.m̅ = a̅.m̅ ⇒ r̅.(8î + 2ĵ− 4k̂) = (−2î + 5ĵ).(8î + 2ĵ− 4k̂ )
⇒ r̅.(4î+ĵ− 2k̂ ) = −3 i.e., 4x + y − 2z + 3 = 0 .
Alterantive : In order to show that the given line x+1/1 = y+1/2 = z+1/3 ….. (i) is coplanar with the line determined by the intersection of the planes π1 : x + 2y + 3z = 8 and π1 : 2x + 3y + 4z =11,
we’ll show that there exists a plane which contains the line (i) and passes through the intersection of planes π1 and π2 .
Eq. of plane through the planes 1 2 π and π is, π: x + 2y + 3z −8+ λ(2x + 3y + 4z −11) = 0…(ii)
If line (i) is on the plane (ii) then, the point on this line (–1, –1, –1) must satisfy the plane (ii).
That is, −1− 2 −3−8+ λ(−2 −3− 4 −11) = 0 ⇒ λ = −7/10
By (ii), we get : π: 4x + y − 2z + 3 = 0…(iii)
Now d.r.’s of the line (i) are 1, 2, 3 and the d.r.’s of normal to the plane (iii) are 4, 1, –2.
Using a1a2 +b1b2 + c1c2 = 0 , we get : 1×4 + 2×1+ 3×(−2) = 0 .
It implies that the line (i) lies in the plane (iii), as the normal to the plane is perpendicular to the line too.
∴ the two lines are coplanar and the equation of plane containing them is 4x + y − 2z + 3 = 0 .
28. A manufacturer makes two types of toys A and B. Three machine are needed for this purpose and the time (in minutes) required for each toy on the machines is given below :

The machines I, II and III are available for a maximum of 3 hours, 2 hours and 2 hours 30 minutes respectively. The profit on each toy of type A is Rs 50 and that of type B is Rs 60. Formulate the above problem as a L. P. P. and solve it graphically to maximize profit.
Sol. Let the manufacturer makes x and y number of toy A and toy B, respectively
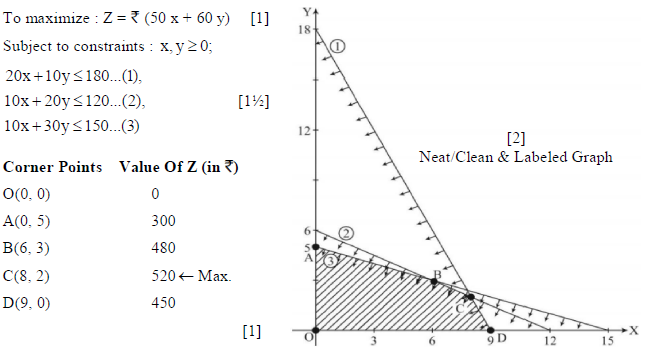
Hence, the maximum profit is Rs 520.
And, nos. of toy A and B are respectively, 8 and, 2.
29. The members of a consulting firm rent cars from three rental agencies :
50% from agency X, 30% from agency Y and 20% from agency Z.
From past experience, it is known that 9% of the cars from agency X need a service and tuning before renting, 12% of cars from agency Y need a service and tuning before renting and 10% of the cars from agency Z need a service and tuning before renting. If the rental car delivered to the firm need service and tuning, find the probability that agency Z is not to be blamed.
Sol. Let E : the car needs service and tuning. Let E1, E2, E3 be the events that car is rented from agency X, Y, Z respectively.
So, P(E1) = 50%, P(E2) = 30%, P(E3) = 20%, P( E |E1) = 9%, P(E | E2) =12%, P(E | E3 ) =10%.