SECTION – A

1. If |A| = 3 and A-1 = 

then write the adj.A.
Solution:

2. For what value of ‘k’, is the function f(x) =

continuous at x = 0 ?
Solution:  

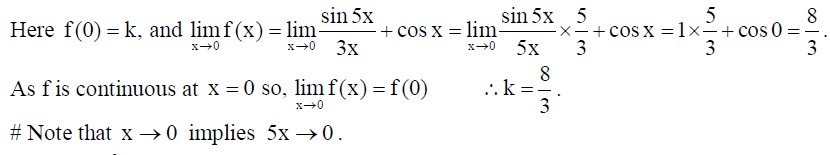
3. Evaluate : 

Solution:  

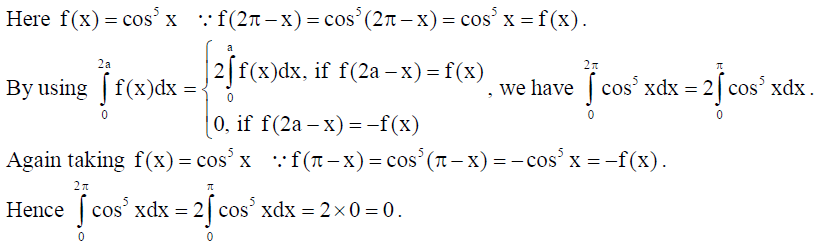
4. Write the distance of the point (3, –5, 12) from x-axis.
Solution: Let A(3, –5, 12). Let B(3, 0, 0) be the foot of perpendicular on x-axis drawn from point A.
So, distance of point A from x-axis is same as the distance AB.
So, AB = √(3-3)² + (-5-0)² + (12-0)² =13 units .

SECTION – B

5. If A and B are square matrices of order 3 such that |A| = –1 and |B| = 3, then find the value of |2AB|.
Solution: |2AB| = 2³ |AB| = 8 |A|| B| = 8(-1)(3) = -24 .
#We have used |kA| = kn |A|, where n is order of A. Also |AB| = |A||B|.

6. The radius r of a right circular cylinder is decreasing at the rate of 3 cm/min and its height h is increasing at the rate of 2 cm/min. When r = 7 cm and h = 2 cm, find the rate of change of the volume of cylinder. [Use π = 22/7] .
Solution: As volume of cylinder is, V = πr2h  ⇒  dV = π(r2 dh/dt + 2hr dr/dt)
When r = 7 cm, h = 2 cm : dV/dt = π(7² x 2 + 2 x 2 x 7 x (-3)) = 22/7 x 7 (14-12) = 44 cm3 min-1 .
Hence volume is increasing at the rate of 44 cm³/min.

7. Find dy/dx at t = 2π/3 when x = 10(t-sin t) and y = 12(1-cos t) .
Solution: Here x = 10(t – sin t) and y = 12(1 – cos t)  ⇒  dx/dt = 10(1-cos t) , dy/dt = 12 sin t 

8. Show that the function f given by f (x) = tan-1(sin x + cos x) is decreasing for all x ∈ (π/4 , π/2) .
Solution:  Here f (x) = tan-1(sin x + cos x)  ⇒  f ‘(x) = 1/1+(sin x + cos x) x (cos x – sin x) = cos x – sin x/2 + sin 2x
As for all x ∈ (π/4 , π/2) , cos x < sin x and 2 + sin 2x > 0
∴ f ‘ (x) = cos x – sin x/2+sin 2x  < 0 for all x ∈ (π/4 , π/2)
∴ f (x) is decreasing on x ∈ (π/4 , π/2) .
# In fact, here f (x) is strictly decreasing on the given interval as f ‘(x) < 0 .    

9. A line passes through the point with position vector 2î – 3ĵ + 4k̂and is perpendicular to the plane r̅.(3î + 4ĵ – 5k̂) = 7 . Find the equation of the line in Cartesian and vector form.
Solution: As the line through the point with position vector 2î – 3ĵ + 4k̂is perpendicular to the plane r̅.(3î + 4ĵ – 5k̂) = 7 so, the line must be parallel to the normal of the plane.
Here normal of the plane is 3î + 4ĵ – 5k̂.
Hence vector eq. of line is : r̅ = 2î – 3ĵ + 4k̂+ λ (3î + 4ĵ – 5k̂) .
Also the Cartesian eq. of line is : x-2/3 = y+3/4 = z-4/-5 .

10. If P(A) = 0.4, P(B) = p, P(A∪B) = 0.6 and A and B are given to be independent events, find the value of ‘p’.
Solution: As P(A∪B) = P(A) + P(B) – P(A∪B)   ⇒   P(A∪B) = P(A) + P(B) – P(A)P(B)
(Since A and B are independent events so, P(A∩B) = P(A)P(B).) 
Now 0.6 = 0.4 + p – 0.4p   ⇒  0.2 = 0.6p  ∴  p = 1/3 .

11. A company produces two types of good A and B, that require gold and silver. Each unit of type A requires 3 g of silver and 1 g of gold while that of type B requires 1 g of silver and 2 g of gold. The company can produce a maximum of 9 g of silver and 8 g of gold. If each unit of type A brings a profit of ₹ 40 and that of type B ₹ 50, formulate LPP to maximize the profit.
Solution: Let the number of units of goods A and goods B be x and y respectively.
To maximize: Z = ₹ (40x + 50y)
Subject to constraints: 3x + y ≤ 9, x + 2y ≤ 8; x, y ≥ 0 .

12. Find 

Solution:  

SECTION – C

13. Find the value of cot 1/2[cos-1 2x/1+x² + sin-1 1-y²/1+y² ] , |x| <1 , y >0 and xy <1 .
Solution:

14. Using properties of determinants, prove that 

= – ((xyz + yz + zx + xy) .
Solution:

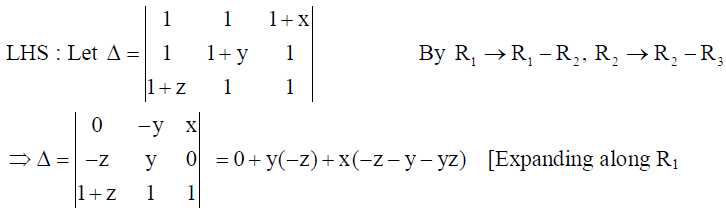
⇒ Δ = – (xyz + yz + zx + xy) = RHS.
# Note that this question was originally in this form : Using properties of determinants, prove

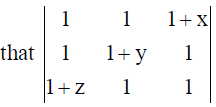
= xyz + yz + zx + xy . Now as –ve sign is missing in RHS, so the equality can’t be proved.
Therefore, full 4 marks may be given to the students for their genuine attempt.

OR

Find matrix X so that 

Solution:

By equality of matrices, we get :
a + 4x = -7, 2a + 5x = -8, 3a + 6x = -9, c + 4d = 2, 2c + 5d = 4, 3c + 6d = 6 .
On solving these equations, we get : a =1, x = -2, c = 2, d = 0 .
Hence

15. If xy = e^(x-y) , then show that dy/dx = y(x+1)/x(y+1) .
Solution: Here xy = e(x-y)…(i)

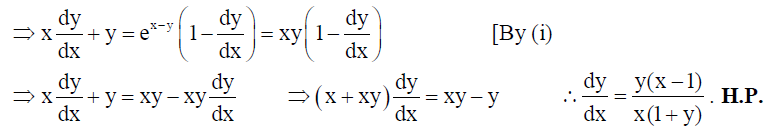
OR

If log y = tan^-1 x , then show that (1+x²) d²y/dx² + (2x-1) dy/dx = 0 .
Solution:

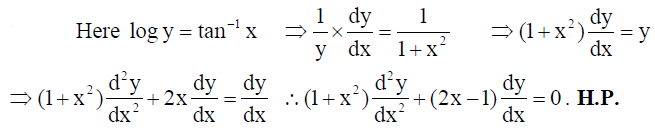
16. Find 

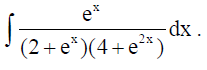
Solution:  

17. Evaluate : 

Solution:  

OR

Evaluate : 

Solution:

18. Find the particular solution of the differential equation 2ye^{x/ y}dx + (y – 2xe^{x/ y} )dy = 0, given that x = 0 when y =1.   
Solution:

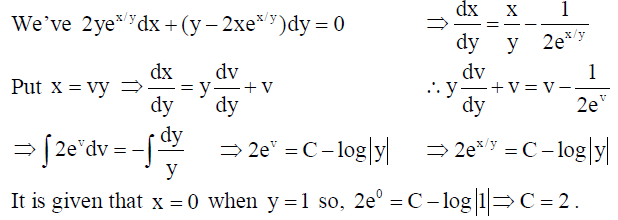
19. Find the area of a parallelogram ABCD whose side AB and the diagonal AC are given by the vectors 3î + ĵ + 4k̂and 4î + 5k̂respectively.
Solution:  

Q20. If a̅ = 2î + ĵ – k̂, b̅ = 4î – 7ĵ + k̂, find a vector c̅ such that a̅ x c̅ = b̅ and a̅.c̅ = 6 .
Solution:

21. There are 4 cards numbered 1 to 4, one number on one card. Two cards are drawn at random without replacement. Let X denote the sum of the numbers on the two drawn cards. Find the mean and variance of X
Solution: Here X : sum of the numbers on the two drawn cards ∴ X can take values 3, 4, 5, 6, 7 .
The probability distribution table is as follows : 

22. In a shop X, 30 tins of pure ghee and 40 tins of adulterated ghee which look alike, are kept for sale while in shop Y, similar 50 tins of pure ghee and 60 tins of adulterated ghee are there. One  tin of ghee is purchased from one of the randomly selected shops and is found to be adulterated.
Find the probability that it is purchased from shop Y. What measures should be taken to stop adulteration?
Solution: Let A : getting adulterated ghee, E₁ : getting ghee from shop X, E₂ : getting ghee from shop Y. 

VBQ : Strong punishment should be given to the shopkeepers indulged in adulteration.

23. Solve the following L.P.P. graphically :
Maxmize : Z = 1000x + 600y
Subject to the constraints : x + y ≤ 200, x ≥ 20, y – 4x ≥ 0, x ≥ 0, y ≥ 0 .
Solution: To Maximize : Z =1000x + 600y
Subject to constraints :
x + y ≤ 200, x ≥ 20,
y – 4x ≥ 0, x ≥ 0, y ≥ 0 

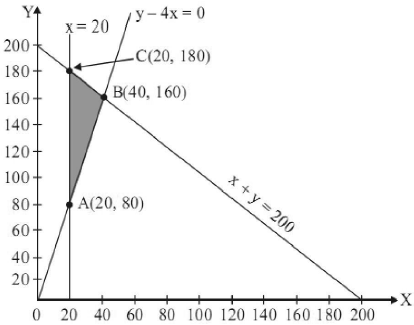
Clearly, Maximum value of Z = 136000
when x = 40 and, y = 160 .

SECTION – D

24. If 

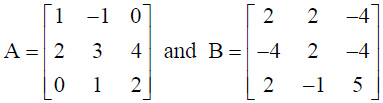
are two square matrices, find AB and hence solve the system of linear equations x – y = 3, 2x + 3y + 4z = 17 and y + 2z = 7 .
Solution:

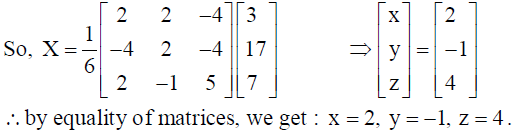
25. Let A = R -{3} , B = R -{1} . Let f :A → B be defined by f (x) = x-2/x-3 ∀ x ∈ A . Show that f is bijective. Also, find
(i) x if f -1(x) = 4 (ii) f -1(7) .
Solution: Given A = R -{3} , B = R -{1} . Let f :A → B be defined by f (x) = x-2/x-3 ∀ x ∈ A 

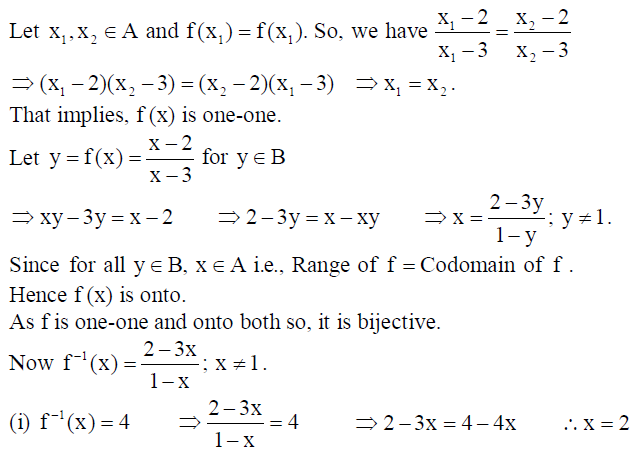
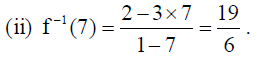
OR

Let A = R x R and let * be a binary operation on A defined by (a, b) * (c, d) = (ad + bc, bd) for all (a, b), (c,d)∈ R x R .
(i) Show that * is commutative on A.
(ii) Show that * is associative on A.
(iii) Find the identity element of * in A.
Solution: Here A = R x R and * is a binary operation on A defined by
(a, b) * (c, d) = (ad + bc, bd) for all (a, b), (c,d)∈ R x R .
(i) Given that (a, b) * (c, d) = (ad + bc, bd)
And, (c, d) * (a, b) = (cb + da, db) = (ad + bc, bd) = (a, b) * (c, d).
Hence * is commutative.
(ii) Let (a, b), (c,d), (e,f )∈ R x R .
Now [(a, b) * (c, d)] * (e, f) = (ad + bc, bd) * (e, f) = (adf + bcf + bde, bdf).
And, (a, b) * [(c, d) * (e, f)] = (a, b) * (cf + de, df) = (adf + bcf + bde, bdf).
Since [(a, b) * (c, d)] * (e, f) = (a, b) * [(c, d) * (e, f)], so * is associative.
(iii) Let (x, y) be the identity element of * in A.
Then, (a, b) * (x, y) = (a, b) = (x, y) * (a, b).
Consider (a, b) * (x, y) = (a, b) ⇒ (ay + bx, by) = (a, b)
By equality of ordered pairs, we get : ay + bx = a, by = b ⇒ y =1, x = 0
Again, consider (x, y) * (a, b) = (a, b) ⇒ (xb + ya, yb) = (a, b)
By equality of ordered pairs, we get : xb + ya = a, yb = b ⇒ y =1, x = 0 .
Hence (0, 1) is the identity element.

26. A wire of length 34 m is to be cut into two pieces. One of the pieces is to be made into a square and the other into a rectangular whose length is twice its breadth. What should be the lengths of the two pieces, so that the combined area of the square and the rectangle is minimum?
Solution: Let the length of one piece be x m (which is used for making a square) and that of other be (34 – x) m (which is used for making a rectangle).
So, the side length of square will be of x/4 m.
For rectangle, 2 (l + b) = 34 – x i.e., 2 (2b + b) = 34 – x i.e., b = 34-x/6 m , where l and b denote the length and breadth of the rectangle respectively.
Now combined area, A = (x/4 ) + 2(34-x/6)²  ⇒  dA/dx = x/8 – 34-x/9
For dA/dx = x/8 – 34-x/9 = 0  ⇒  9x = 34 x 8  ⇒  x = 16
Also, d²A/dx² = 1/8 + 1/9 > 0 , so, A is minimum when x = 16 m.
Hence the lengths of two pieces are 16 m and 18 m.

27. Using the method of integration, find the area of the triangle ABC, coordinates of whose vertices are A(1, 2), B(2, 0) and C(4, 3).
Solution: Here the vertices are A(1, 2), B(2, 0) and C(4, 3).
Hence equations of sides are : 

⇒  = 7/2 sq.units .

OR

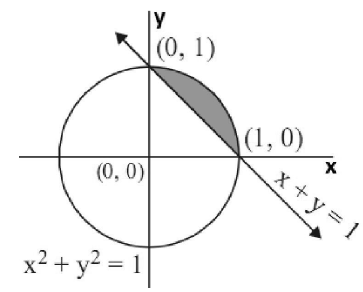
Using integration, find the area of the region {(x, y) : x² + y² ≤1≤ x + y}.
Solution: {(x, y) : x² + y² ≤1≤ x + y}
Consider x² + y² =1, x + y =1.
Solving these equations, we get : 

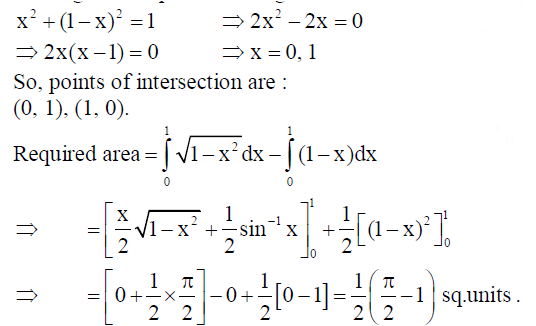
28. Find the particular solution of the differential equation dy/dx -3 ycot x = sin 2x , given that y = 2 when x = -π/2 .
Solution: Given differential equation can be rewritten as dy/dx -3 ycot x = sin 2x , given that y = 2 when x = -π/2
This is linear differential equation of the form dy/dx + yP(x) = Q(x) , where
P(x) = – 3cot x,Q(x) = sin 2x . 

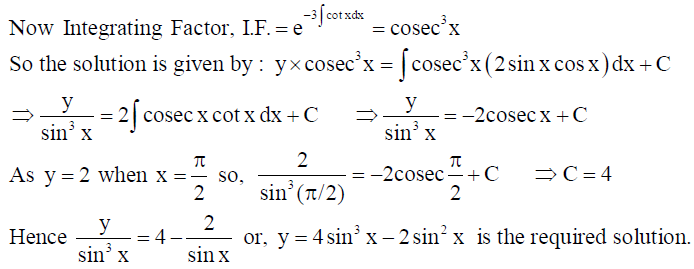
29. Find the vector equation of the plane through the line of intersection of the planes x + y + z =1 and 2x + 3y + 4z = 5 which is perpendicular to the plane x – y + z = 0 . Hence find whether the plane thus obtained contains the line x+2/5 = y-3/4 = z/5 or not   
Solution: The required plane is π : x + y + z -1+ λ(2x + 3y + 4z -5) = 0
⇒ π:x(1+ 2λ) + y(1+ 3λ) + z(1+ 4λ) – (1+ 5λ) = 0…(i)
As (i) is ⊥^er to the plane x – y + z = 0 so, 1(1+ 2λ) – (1+ 3λ) +1.(1+ 4λ) = 0 ⇒ λ = -1/3
Replacing this value of λ in (i), we get : x – z + 2 = 0…(ii)
In vector form, the plane is r̅.(î – k̂) + 2 = 0 .
Given line can be rewritten as x-(-2)/5 = y-3/4 = z-0/5 . Therefore, point on the line is (–2, 3, 0).
LHS of (ii) : x – z + 2 = -2 – 0 + 2 = 0 = RHS .
Also, 1×5 + 0x 4 – 1×5 = 0  [∴ a₁a₂ + b₁b₂ + c₁c₂ = 0 here implies that the line is ⊥^er to plane .
Hence the given line lies on the plane (ii).

OR

Find the image P’ of the point P having position vector î + 3ĵ + 4k̂ in the plane r̅.(2î – ĵ + k̂) + 3 = 0 . Hence find the length PP’ .
Solution: Here P(î + 3ĵ + 4k̂) i.e., P(1, 3, 4). Let π : r̅.(2î – ĵ + k̂) + 3 = 0 i.e., -2x + y – z = 3 .
Draw PA⊥er  to plane π. So, clearly PA will be parallel to the Normal of the plane π.
∴ Eq. of PA : x-1/-2 = y-3/1 = z-4/-1 = λ (say) .
The coordinates of any random point on line PA are A(-2λ +1, λ + 3, – λ + 4) .
This point must lie on plane π for some specific value (s) of λ .
Therefore, -2.(-2λ +1) +1.(λ + 3) -1.(-λ + 4) = 3 ⇒ λ = 1.
Hence foot of perpendicular of P on the plane is A(–1, 4, 3).
Let the image of P in the plane be at P’ (h, p, s).
Clearly A will be the mid-point of P P’ . Hence A(h+1/2 , p+3/2 , s+4/2) = A (-1 , 4 , 3)
On comparing the coordinates, we get : h = -3, p = 5, s = 2 .
Therefore the required image is P'(-3, 5, 2) .
Now PP’ = √42 + (-2)2 + 22 = 2√6 units .