Please refer to Sample Paper Class 12 Mathematics Term 2 Set E with solutions provided below. We have provided CBSE Sample Papers for Class 12 Mathematics as per the latest paper pattern and examination guidelines for Standard 12 Mathematics issued by CBSE for the current academic year. The below provided Sample Guess paper will help you to practice and understand what type of questions can be expected in the Class 12 Mathematics exam.

CBSE Sample Paper Class 12 Mathematics for Term 2 Set E

1.

Answer. Let

2. Using separable form,

Now, integrating them.
Answer. Given that,

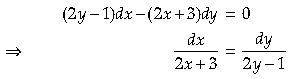
3. Direction cosines are:
l = cos a, m = cos a, n = cos a
∴ a = b = g
Answer. Direction cosines of a line making angle, a with x-axis, β with y-axis and γ with z-axis are l, m, n.
Where, l = cosα, m = cosβ, n = cos γ
Given, the line makes equal angles with coordinate axes.
So, a = b = g                    …(i)
Direction cosines are:
l = cosa, m = cosa, n = cosa
Since,

4.

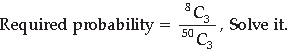
Answer. Since there are only 8 number (in first 50 natural numbers) which are divisible by 6.
∴ Favorable number of outcomes are ⁸C₃. 
Total number of possible outcomes are ⁵⁰C₃.

5.

Answer. Given that,

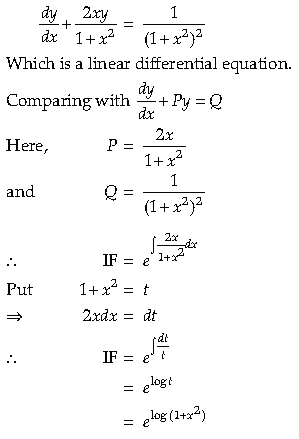
6.

Answer. The given definite integral

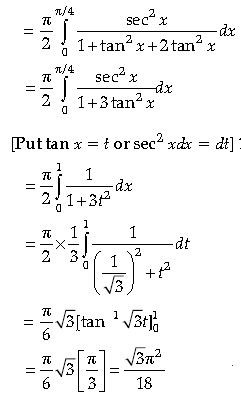
7.

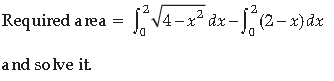
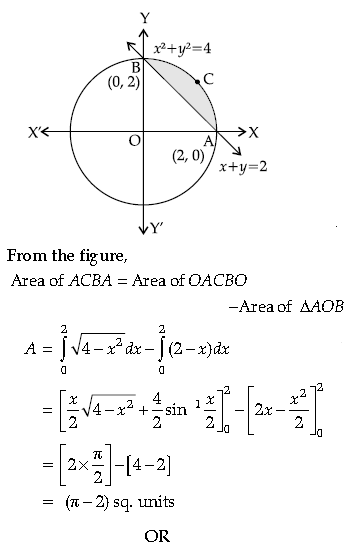
Answer. The smaller area enclosed by the circle
x² + y² = 4 and the line, x + y = 2 is
represented by the shaded area ACBA as :

It is given that we have to find the area bounded by the curve y = x³, the x-axis and the ordinates x = – 2 and x = 1.
First of all, draw the curve y = x³ and
x = – 2 the ordinary x = 1. Then highlight the bounded portion between the curve and the ordinates. Which is shown in the figure.

Now, calculate the area of the bounded figure by breaking the curve in two parts: the first part is the curve between x = – 2 and
x = 0, and the second part is the curve between
x = 0 and x = 1.
We have studied that the area bounded by the curve and x-axis is given by

Given ordinates bound the curve on the left and right side which gives the upper and lower limits of the integration.
Now, the area of bounded figure is given by

8.

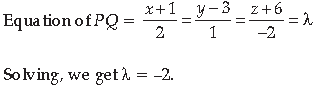
Answer. Let P be the given point and Q be the foot of the perpendicular

Let coordinates of Q be (2λ – 1, λ + 3, –2λ – 6)
Since Q lies in the plane 2x + y – 2z + 5 = 0 1
∴ 2(2λ – 1) + (λ + 3) – 2(–2λ – 6) + 5 = 0
⇒ 4λ – 2 + λ + 3 + 4λ+ 12 + 5 = 0
⇒ 9λ + 18 = 0
⇒ λ = – 2 1
∴ Coordinates of Q are (–5, 1, –2)
Length of the perpendicular from P to the plane