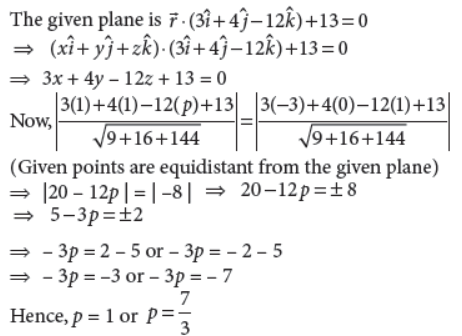Sample Paper Class 12 Mathematics Set C
PART – A
Section – I
1. If
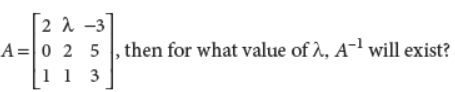
Answer : We know that A–1 exists if |A| ≠ 0.

OR
Find the values of x for which
Answer : We have, 3 – x2 = 3 – 8 ⇒ x2 = 8
⇒ x = ±2√2
2. Show that the function f : R → R, given by f(x) = |x| is neither one-one nor onto.
Answer : Since, f(1) = f(–1) = 1, therefore f is not one-one.
Also, Range (f ) = [0, ∞) ≠ R, therefore f is not onto.
3. Find the direction cosines of the perpendicular from the origin to the plane r̅.(2î – 3ĵ –6k̂) = 5
Answer : The perpendicular from the origin to plane
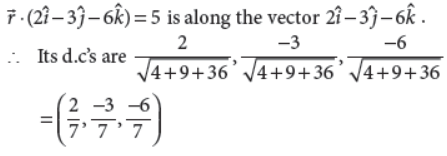
OR
Find the equation of plane passing through the point (1, 2, 3) and the direction cosines of the normal as l, m, n.
Answer : Equation of plane passing through (1, 2, 3) having direction cosines of normal as l, m, n is
l(x – 1) + m(y – 2) + n(z – 3) = 0
⇒ lx + my + nz = l + 2m + 3n
4. Check whether the matrix

Answer :
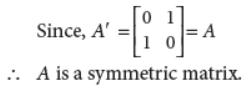
5. Evaluate :
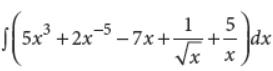
Answer :
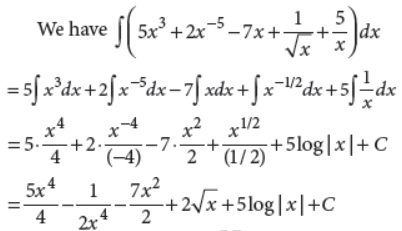
OR
Evaluate :
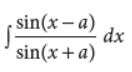
Answer :
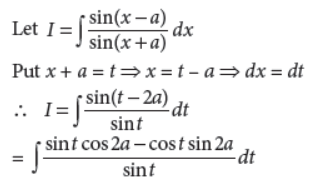

6. Find the number of bijective functions from set A to itself when A contains 106 elements.
Answer : The total number of bijections from a set containing n elements to itself is n!
Hence, required number = (106)!
7. If a̅ =2î + ĵ + 3k̂ and b̅ =3î + 5ĵ – 2k̂ then find |a̅ .b̅|
Answer :

OR
Find the value of λ so that the vectors 2î – 4ĵ + k̂ and 4î – 8ĵ + λk̂ are perpendicular.
Answer : The given vectors will be at right angles if their dot product vanishes, i.e.,
(2î – 4ĵ + k̂).(4î – 8ĵ + λk̂) = 0
⇒ 8 + 32 + λ = 0 ⇒ λ = –40
8. Evaluate :

Answer :
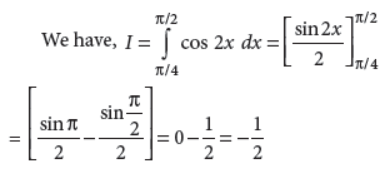
9. Write the direction cosines of a line parallel to z-axis.
Answer : We know that, two parallel lines have same set of direction cosines. Therefore, required direction
cosines are the direction cosines of Z-axis, i.e., 0, 0, 1
10. Determine the order and degree of

Answer : The given differential equation can be written as

OR
Find the integrating factor of the differential equation dy/dx+(secx)y=tanx.
Answer :
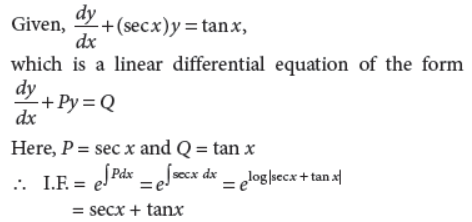
11. Let a̅ and b̅ are non-collinear. If c̅ = (x–2)a̅+ b̅ and d̅ = (2x +1)a̅−b̅ are collinear, then find x.
Answer : Given, c̅ = (x–2)a̅+ b̅ and d̅ = (2x +1)a̅−b̅ are collinear, therefore c̅ = md̅
⇒ (x–2)a̅+b̅ = m(2x+1)a̅–b̅)
⇒ m = –1
and m (2x + 1) = x – 2 ⇒ – 2x – 1 = x – 2 ⇒ x = 1/3
12. Find the equation of the plane with intercept 2, 3 and 4 on the x,y and z-axis, respectively.
Answer : Here, a = 2, b = 3 and c = 4
∴ Required equation of plane is x/2 + y/3 +z/4 =1.
⇒ 6x + 4y + 3z = 12,
which is the required equation of plane.
13. Let f : R → R be defined by
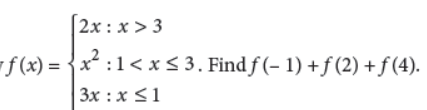
Answer : Clearly f(–1) = 3(–1) = –3 ;
f(2) = (2)2 = 4 and f(4) = 2(4) = 8
∴ f(–1) + f(2) + f(4) = –3 + 4 + 8 = 9
14. The equation of a line is 5x – 3 = 15y + 7 = 3 – 10z. Write the direction cosines of the line.
Answer : The given equation of line can be written in standard form as

15. Find the projection of the vector î +3ĵ + 7k̂ on the vector 2î –3ĵ + 6k̂.
Answer : Let a̅ = î +3ĵ + 7k̂ and b̅ = 2î –3ĵ + 6k̂.
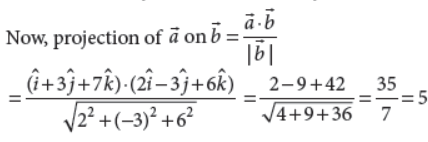
16. If

Answer :

Section – II
Case study-based questions are compulsory. Attempt any 4 sub parts from each question. Each sub-part carries 1 mark.
17. Ajay wants to construct a rectangular fish tank for his new house that can hold 72 ft3 of water. The top of the tank is open. The width of tank will be 5 ft but the length and heights are variables. Building the tank cost 10 per sq. foot for the base and 5 per sq. foot for the side.
Based on the above information, answer the following question :

(i) In order to make a least expensive fish tank, Ajay need to minimize its
(a) Volume
(b) Base
(c) Curved surface area
(d) Cost
Answer : D
(ii) Total cost of tank as a function of h can be represented as
(a) c(h) = 50 h – 144 – 720/h
(b) c(h) = 50 h – 144 h – 720 h2
(c) c(h) = 50 + 144 h + 720 h2
(d) c(h) = 50 h + 144 + 720/h
Answer : D
(iii) Range of h is
(a) (3, 5)
(b) (0, ∞)
(c) (0, 8)
(d) (0, 3)
Answer : B
(iv) Value of h at which c(h) is minimum, is
(a) √14.4
(b) √12.2
(c) 14.5
(d) 12.5
Answer : A
(v) The cost of least expensive tank is
(a) 500
(b) 502.04
(c) 523.47
(d) 600.05
Answer : C
18. A night before sleep, grandfather gave a puzzle to Rohan and Payal. The probability of solving this specific puzzle independently by Rohan and Payal are 1/2 and 1/3 respectively.
Based on the above information answer the following :

(i) Probability that both solved the puzzle, is
(a) 1/2
(b) 1/3
(c) 1/6
(d) 5/6
Answer : C
(ii) Probability that puzzle is solved by Rohan but not by Payal, is
(a) 1/2
(b) 1/6
(c) 3/5
(d) 1/3
Answer : D
(iii) Find the probability that puzzle is solved.
(a) 1/2
(b) 1/3
(c) 2/3
(d) 5/6
Answer : C
(iv) Probability that exactly one of them solved the puzzle.
(a) 1/3
(b) 1/2
(c) 1/6
(d) 5/6
Answer : B
(v) Probability that none of them solved the puzzle.
(a) 1/2
(b) 1/3
(c) 2/3
(d) None of these
Answer : B
PART – B
Section – III
19. Find the area enclosed by the line y = 3x, the x-axis, and the ordinates x = 1 and x = 4.
Answer : Area enclosed by line y = 3x, x-axis, x = 1 and x = 4 is shown in figure.
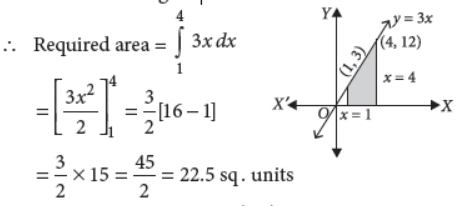
20. Find the principal value of cos-1(-1/2)+2sin-1(-1/2).
Answer :
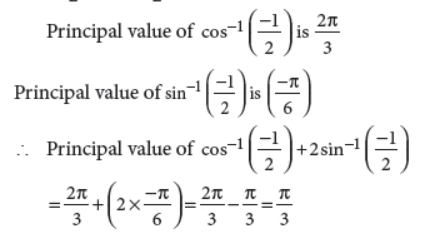
OR
Find the two branches other than the principal value branch of tan–1x.
Answer : We known that, principal value branch of tan–1x is

21. A coin is tossed and then a die is thrown. Find the probability of obtaining a ‘6’ given that head came up.
Answer : The sample space S associated to the given random
experiment is given by
S = {(H, 1), (H, 2), (H, 3), (H, 4), (H, 5), (H, 6), (T, 1),
(T, 2), (T, 3), (T, 4), (T, 5), (T, 6)} and
Let the event B = {(H, 6), (T, 6)} and
A = {(H, 1), (H, 2), (H, 3), (H, 4), (H, 5), (H, 6)}
∴ Required probability = P(B | A)

22. If

Answer :
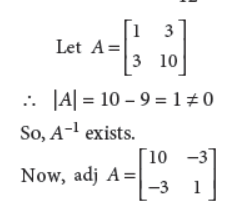
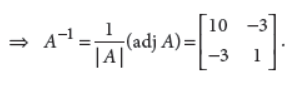
23. Evaluate :

Answer :
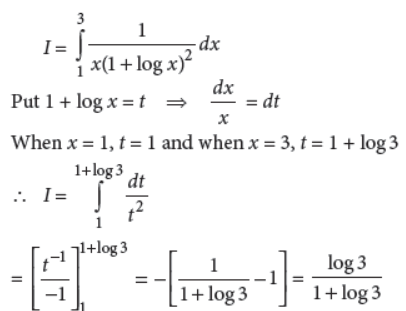
OR
Evaluate :

Answer :

24. If y = cotx, then show that d2y/dx2 + 2y dy/dx = 0.
Answer :
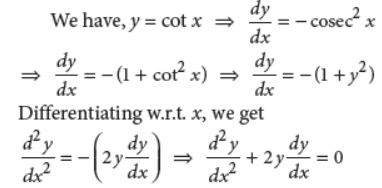
25. Find the order and degree of the differential equation given by
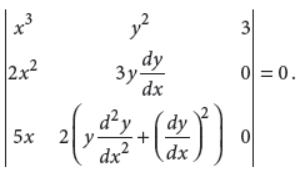
Answer :

26. Find the point at which the tangent to the curve y = √(4x − 3 )− 1 has its slope 2/3 .
Answer : Slope of tangent to the given curve at (x, y) is

27. A couple has 2 children. Find the probability that both are boys, if it is known that
(i) one of them is a boy,
(ii) the older child is a boy.
Answer : Let Bi(i = 1, 2) denote the ith child is a boy and
Gi(i = 1, 2)denote the ith child is a girl respectively.
Then sample space is,
S = {B1B2, B1G2, G1B2, G1G2}
Let A be the event that both are boys, B be the event
that one of them is a boy and C be the event that the
older child is a boy.
A = {B1B2}, B = {G1B2, B1G2, B1B2}
C = {B1B2, B1G2} ⇒ A∩B = {B1B2} and A∩C = {B1B2}
(i) Required probability = P(A|B)

28. If A, B, C have position vectors (2, 0, 0), (0, 1, 0), (0, 0, 2), show that DABC is isosceles.
Answer :
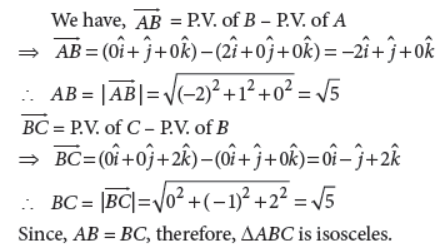
OR
If a̅ × b̅ = c̅ × d̅ and a̅ × c̅ = b̅ × d̅ , then show that (a̅ − d̅) is pa̅ra̅llel to (b̅ − c̅) , it is being given that a̅ ≠ d̅ and b̅ ≠ c̅ .
Answer :
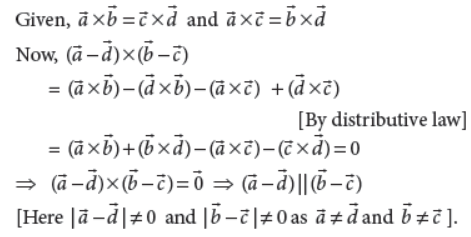
Section – IV
29. Find the equations of tangent and normal to the curve 2x2 + 3y2 – 5 = 0 at (1, 1).
Answer : We have, 2x2 + 3y2 – 5 = 0 …(i)
Differentiating both sides w.r.t. x, we get
4x+6x dy/dx–0 = 0

30. Show that the family of curves for which the slope of the tangent at any point (x, y) on it is x2+y2/2xy is given by x2 – y2 = Cx.
Answer :
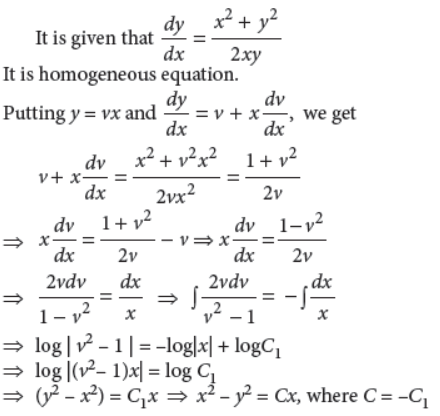
31. Determine the values of a, b and c for which the function
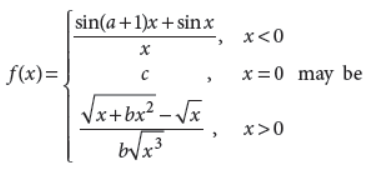
Answer :

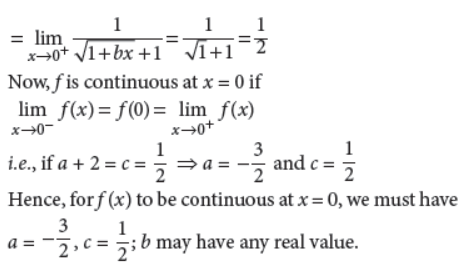
OR

32. Find the area bounded by the curve y = sinx between x = 0 and x = 2π.
Answer : The given curve is y = sinx

33. Let P be the set of all the points in a plane and the relation R in set P be defined as R = {(A, B) ∈ P × P | distance between points A and B is less than 3 units}. Show that the relation R is not an equivalence relation.
Answer : Given, R = {(A, B) ∈ P × P | distance between points A and B is less than 3 units}
For reflexivity : (A, A) ∈ R is true as distance between points A and A is 0, which is less than 3 units for all A ∈ P. Hence, R is reflexive.
For symmetry : Let A, B ∈ P and (A, B) ∈ R ⇒ distance between points A and B is less than 3 units.
⇒ Distance between B and A is less than 3 units.
So, (B, A) ∈ R
Hence, R is symmetric.
For transitivity : Let points A, B and C are collinear. B is mid-point of AC such that distance between A and B is 2 units and between B and C is also 2 units, i.e.,
(A, B) ∈ R and (B, C) ∈ R, we notice distance between
A and C is 4 units ⇒ (A, C) ∉ R. Hence, R is not transitive.
Hence, R is not an equivalence relation.
34. Evaluate :

Answer :
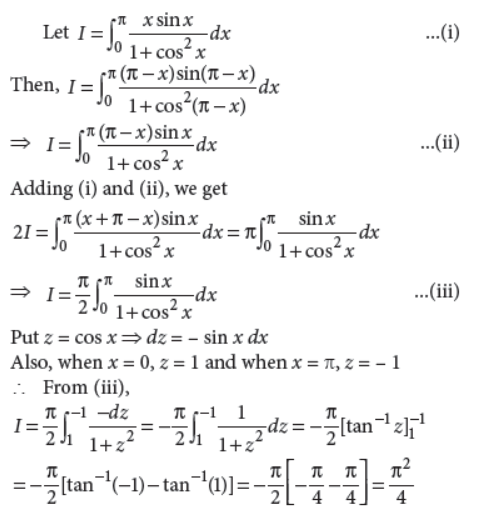
OR
Evaluate :

Answer :

35. If x = a(cos 2θ + 2θ sin 2θ) and y = a(sin 2θ− 2θ cos 2θ), then find d2y/dx2 at θ = π/8.
Answer : Given, x = a(cos 2θ + 2θ sin 2θ)

Section – V
36. Solve the following problem graphically.
Minimize Z = 4x/1000 + 6y/1000
subject to constraints :
0.1 x + 0.05 y ≤ 50
0.25 x + 0.5 y ≥ 200
x, y ≥ 0
Answer : The given problem is
Minimize Z = 4x/1000 + 6y/1000
Subject to constraints:
0.1 x + 0.05 y < 50
0.25 x + 0.5 y ≥ 200
x, y ≥ 0
Convert the inequations into equations and draw the graph of lines:
0.1x + 0.05y = 50 ; 0.25x + 0.5y = 200

As x ≥ 0, y ≥ 0 \ Solution lies in first quadrant
Here, the shaded region is the feasible region. Now, we find the value of Z at each corner point.

OR
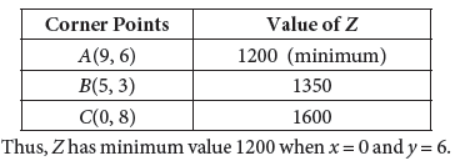
Solve the following problem graphically.
Minimize Z = 150x + 200y
subject to constraints :
6x + 10y ≥ 60
4x + 4y ≤ 32
x, y ≥ 0
Answer : The given problem is
Minimize Z = 150x + 200y
subject to constraints
6x + 10y ≥ 60 ;
4x + 4y ≤ 32 ; x ≥ 0, y ≥ 0
As x ≥ 0, y ≥ 0 \ Solution lies in first quadrant

Convert the inequations into equations and draw the graph of lines:
6x + 10y = 60 ; 4x + 4y = 32
Here, shaded region is the feasible region.
Corner points of feasible region are A(0, 6), B(5, 3)
and C(0, 8).
Value of Z at these corner points are:
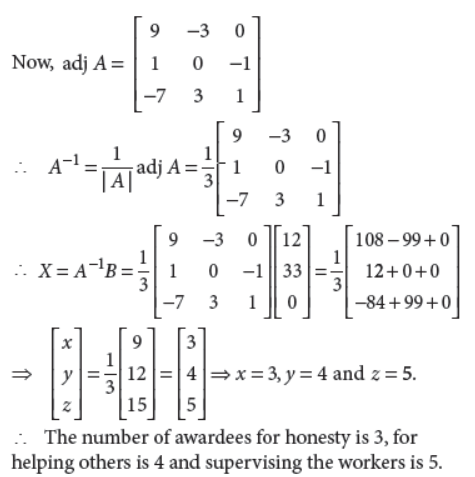
37. The management committee of a residential colony decided to award some of its members (say x) for honesty, some (say y) for helping others and some others (say z) for supervising the workers to keep the colony neat and clean. The sum of all the awardees is 12. Three times the sum of awardees for helping others and supervision added to two times the number of awardees for honesty is 33. If the sum of the number of awardees for honesty and supervision is twice the number of awardees for helping others, using matrix method, find the number of awardees of each category.
Answer : According to given conditions, we have
x + y + z = 12, 2x + 3(y + z) = 33, x + z = 2y
i.e., x + y + z = 12, 2x + 3y + 3z = 33, x – 2y + z = 0.
The given system of equations can be written as
AX = B
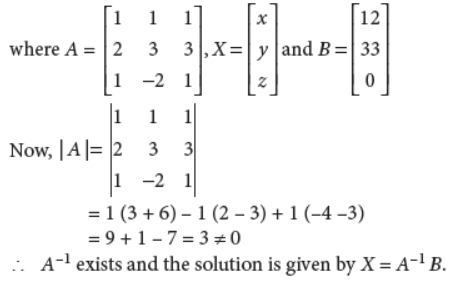
OR
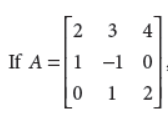
then find A–1. Hence, solve the system of equations 2x + 3y + 4z = 17; x − y = 3;y + 2z = 7.
Answer :

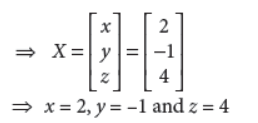
38. Find the shortest distance between the lines x–1/2 = y–2/3 = z–3/4 and x–2/3 = y–4/4 = z–5/5.
Answer : The equation of two given lines are

OR
If the points (1, 1, p) and (–3, 0, 1) be equidistant from the plane r̅.(3î + 4ĵ –12k̂) + 13 = 0 then find the value of p.
Answer :