Section A

1. Find (576 + 789)mod 9.
(a) 0
(b) 6
(c) 7
(d) 8

2. The least non-negative remainder when 3242 is divided by 13 is
(a) 3
(b) 6
(c) 9
(d) 1

3.

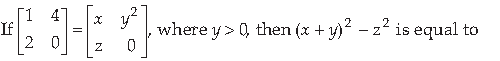
(a) 0
(b) 5
(c) – 1
(d) 3

4. If A is a non-singular 3 x 3matrix and B is its adjoint such that |B|= 81, then |A| is equal
to
(a) 81
(b) ±9
(c) ±10
(d) 15

5.

(a) 1
(b) 2
(c) 6
(d) 11

6. The interval in which the function f (x) = 10 – 6x – 2x² is decreasing is

7. The two numbers whose sum is 40 and whose product is as large as possible, are
(a) 10 and 30
(b) 20 and 20
(c) 15 and 25
(d) 18 and 22

8. The slope of tangent to the curve x² + 3y + y² = 5 at (1, 1) is equal to
(a) 2/5
(b) 5/2
(c) – 2/5
(d) – 5/2

9. An index that is designed to measure changes in quantities over time is known as the
(a) time index
(b) Paasche’s index
(c) quantity index
(d) Fisher’s index

10. Cost of living at two different cities can be compared with the help of
(a) wholesale price index
(b) consumer prices index
(c) value index
(d) None of these

11. For the given data ∑p₀w = 5246 and ∑p₁w = 6481, where subscript 0 and 1 are used for base year and current year respectively, the index number by using weighted aggregates method is
(a) 120.42
(b) 123.54
(c) 115.62
(d) 118.42

12. In a game of 620 points, A score 560 points, while Awin by 70 points. In the game, how many points B scores
(a) 500
(b) 690
(c) 490
(d) 530

13. The probability distributions of the number of successes in two tosses of a die, where a success is defined as six appears on atleast one die respectively are

14. When a die is thrown thrice, getting an odd number is considered a success. The variance of the Binomial distribution is 
(a) 1/4
(b) 1/2
(c) 3/4
(d) 1

15. There are 600 business students in the graduate department of a university and the probability for any student to need a copy of a particular textbook from the university library on any day is 0.05. The number of copies of the book should be kept in the university library so that the probability may be greater than 0.90 that none of the students needing a copy from the library has to come back disappointed are
(a) 32
(b) 34
(c) 37
(d) 35

16. Let X be a standard normal variate. The value of t, if P(z ≤ t) = 0.7357, is
(a) 0.27
(b) 0.53
(c) 0.83
(d) 0.63

17. If x ae= t and y ae = -t , then dy/dx is equal to
(a) e ^-t
(b) – e ^-t
(c) e ^-2t
(d) – e ^-2t

18. A person can row with the stream at 8 km/h and against the stream at 6 km/h. The speed of the current is
(a) 1 km/h
(b) 2 km/h
(c) 4 km/h
(d) 5 km/h

19. Two pipes A and B can fill a tank in 24 min and 32 min respectively. If both the pipes are opened simultaneously, after x min should B be closed so that the tank can be filled in 18 min. The value of x is
(a) 2
(b) 4
(c) 6
(d) 8

20. The solution set of the inequality |x – 7|< 2 is
(a) (3, 7)
(b) (5, 9)
(c) (8, 9)
(d) (- 5, – 9)

Section B

21. The unit’s digit in 183 3183 ! + is
(a) 0
(b) 3
(c) 6
(d) 7

22. Which of the following statement is not true?
(a) 27 ≅ 3(mod4)
(b) 11 ≅ 56(mod9)
(c) – 4 ≅ -114(mod11)
(d) 15 ≅ 3(mod9)

23.

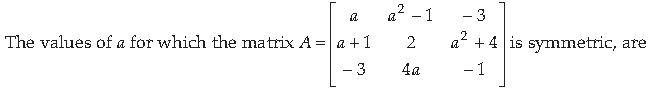
(a) – 1
(b) – 2
(c) 3
(d) 2

24.

(a) 1 + x + y + z
(b) x + y + z
(c) 0
(d) 1

25.

26. The manufacturing cost of an item consists of ₹ 900 as overheads, the material cost is
₹ 3 per item and labour cost ₹ x²/100 for x items produced. The number of items produced
to have average cost minimum is
(a) 100
(b) 200
(c) 300
(d) 400

27. The slope of the tangent to the curve y = x ³ – 3x + 2 at the point (3, 0), is
(a) 6
(b) 12
(c) 24
(d) 36

28. The price and quantities of certain commodities are shown in the following table

If ratio of Laspeyre’s (L) and Paasche’s (P) index number i.e. L:P = 65 :72, then valueof x is 
(a) 1
(b) 2
(c) 3
(d) 4

29. For the given data, ∑p₀ q₀ = 6643, ∑p₁q₀ = 6702, ∑p₀ q₁ = 6842 and ∑p₁q1 = 7041, where subscript 0 and 1 are used for base year and current year respectively. The Laspeyre’s index number is
(a) 100.89
(b) 102.41
(c) 98
(d) 99

30. For data regarding some commodities the price indexes using Laspeyre’s and Paasche’s method are 142.6 and 146.2 respectively. The fisher’s price index for the data is
(a) 154.34
(b) 144.39
(c) 160.5
(d) 148.52

31. Increasing in the wholesale price index over a long period of time implies
(a) inflation
(b) higher money wages
(c) Both (a) and (b)
(d) None of these

32. Given that ∑p₁q₁ = 266, ∑p₀ q₀ = 212, ∑p₁q₀ = 284, and ∑p₀ q₁ = 235, where subscript 0 and 1 are used for base year and current year respectively. The Paasche’s index number is
(a) 113.15
(b) 113.19
(c) 123.4
(d) 115.40

33. If ten coins are tossed, then the probability of getting atleast 8 heads, is
(a) 7/128
(b) 6/128
(c) 5/128
(d) 4/128

34. The probability distribution of a random variable X is given as under

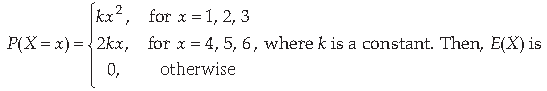
(a) 97/22
(b) 47/22
(c) 93/22
(d) 95/22

35. Poisson distribution is used to describe a situation where 200 misprint are distributed randomly through 500 pages. The probability that a given page contain exactly 2 misprint is
(a) 0.0632
(b) 0.062
(c) 0.0536
(d) 0.0413

36. In a sample of 10000 items, the mean weight is 30 kg with a standard deviation 10 kg.
Assuming the normality of the distribution, the number of items weighing between 30 and 45 kg is
(a) 5423
(b) 4332
(c) 3672
(d) 2430

37.

(a) 1
(b) – 1
(c) e^{x + y}
(d) 0

38. A boat travels 16 km downstream in 4 h and 12 km upstream in 6 h. The speed (in km/h) of boat in still water is
(a) 1
(b) 2
(c) 3
(d) 4

39. Radha started a business by investing ₹ 75000. After 3 months, Sunidhi joined her with an amount of ₹ 125000 and after another six months, Neha joined them with an amount of ₹ 150000. Profit earned at the end of three years from when Radha started the business should be distributed among Radha, Sunidhi and Neha, respectively in the ratio
(a) 36: 55: 54
(b) 18:28:27
(c) 35:54: 55
(d) Cannot be determined

40. A container has 30 L of water. If 3 L of water is replaced by 3 L of spirit and this operation is further repeated twice, then the quantity of water in the new mixture is
(a) 24 L
(b) 21.87 L
(c) 24.3 L
(d) 23.3 L

Section C

41. Let X be a discrete random variable whose probability distribution is defined as follows,

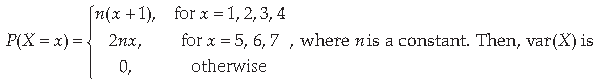
(a) 1.92
(b) 2.92
(c) 3.92
(d) None of these

42. If a set of observations are normally distributed, then the percentage of the measurements which differ from the mean by more than half the standard deviation is
(a) 62%
(b) 61.7%
(c) 63.8%
(d) 57.8%

43. The remainder when 862 ´783 ´ 671 ´ 549 ´ 411 ´ 395 is divided by 8 is
(a) 0
(b) 3
(c) 6
(d) 7

44. If f (x) = a log |x|+ bx ² + x has extreme values at x = – 1 and x = 2, then (a, b) is equal to

45. If pipe A is 6 times faster than pipe B and can fill a tank in 25 min less than pipe B, then
the time taken to fill the tank when both pipes are opened together is

Case Study

If A= [a_ij ] be an m´ nmatrix, then the matrix obtained by interchanging the rows and columns of Ais called the transpose of A.
A square matrix A a_ij = [ ] is said to be symmetric, if A A T = for all possible values of i and j.
A square matrix A aij = [ ] is said to be skew-symmetric, if A A T = – for all possible values of i and j.
Based on above information, answer the following questions.

46. The transpose of matrix [1 – 2 – 5] is

47. (ABC)T is equal to
(a) C^T B^T A^T
(b) A^T B^T C^T
(c) B^T A^T C^T
(d) B^T C^T A^T

48. For any square matrix A with real number entries)
(a) A + A^T is skew-symmetric matrix
(b) A + A^T is symmetric matrix
(c) A + A^T is symmetric as well as skew-symmetric matrix
(d) None of the above

49. Any square matrix can be expressed as
(a) difference of a symmetric and a skew-symmetric matrix
(b) sum of two symmetric matrices
(c) sum of a symmetric and a skew-symmetric matrix
(d) sum of two skew-symmetric matrices

50. If A and B are symmetric matrices of same order, then AB = BA is a
(a) skew-symmetric matrix
(b) symmetric matrix
(c) zero matrix
(d) identity matrix