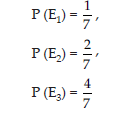Please refer to Sample Paper Class 12 Mathematics Term 2 Set B with solutions provided below. We have provided CBSE Sample Papers for Class 12 Mathematics as per the latest paper pattern and examination guidelines for Standard 12 Mathematics issued by CBSE for the current academic year. The below provided Sample Guess paper will help you to practice and understand what type of questions can be expected in the Class 12 Mathematics exam.

CBSE Sample Paper Class 12 Mathematics for Term 2 Set B

Section – A

1. A bag contains 5 red, 7 green and 4 white balls. Three balls are drawn one after the other without replacement. Find the probability that the balls drawn are white, green and green respectively.
Answer: 1. A bag has 5 red, 7 green and 4 white balls.
So, Total balls = 5 + 7 + 4 = 16
P(White, green and green) = P(White). P(green/white).P(green/white and green)
4/16×7/15×6/14=1/20

2. Find the direction cosines of the line passing through the two points (–1, 2, 3) and (2, –3, 5).
Answer: We know that the direction cosines of a line joining two points P and Q are given by

3. Find∫(cos6x∫1+sin6xdx
OR
Find: ∫(x+1/x)2dx.
Answer: 

4. From a pack of 52 cards, two cards are drawn together at random. What is the probability of both the cards being queens?
Answer:  Total number of ways of getting two cards,

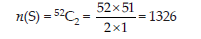
Let E be the event of getting two queens out of 4.

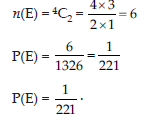
5. a^→ b^→ and c^→are unit vectors such that 2 a^→ 3 b^→ 4 c^→= 0 and the angle between a^→and b^→is θ, find the value of (4 cos θ – 1).
Answer:

Taking dot product with itself

6. Find the order and degree of the following differential equation:

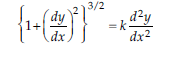
Answer: The highest derivative occuring in the differential equation

Which is of order 2. Hence the order of the differential equation is 2.
The equation

Raising both sides of the powre 2 we have,

The exponent of the highest order derivative, i.e., d² y/dx² is 2. Thus the degree of the equation is 2.

Section – B

7. Find the shortest distance between the following pairs of lines:
x-8/3=y-5/-2=z-10/7 and x-15/3=y+1/8=z-5/-5
OR
Find the value of λ, so that the following lines are perpendicular to each other:
x+5/5λ+2=2-y/5=1-z/-1and x/1=2y+1/4λ=1-z/-3
Answer: Given equation of two lines
x-8/3=y-5/-2=z-10/7″ ……..(1)
and x-15/3=y+1/8=z-5/-5 ……(2)
Line (1) passes through (8, 5, 10) and has direction ratios proportional to 3, – 2, 7, So its vector equation is

Line (2) passes through (15, – 1, 5) and has direction ratios 3, 8, – 5, so its vector equation is

Now,

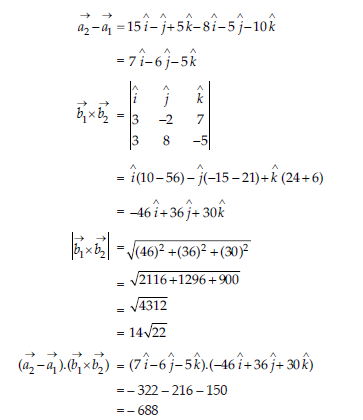
The shortest distance between the lines

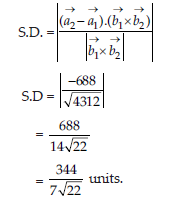
OR
Given equation of lines are

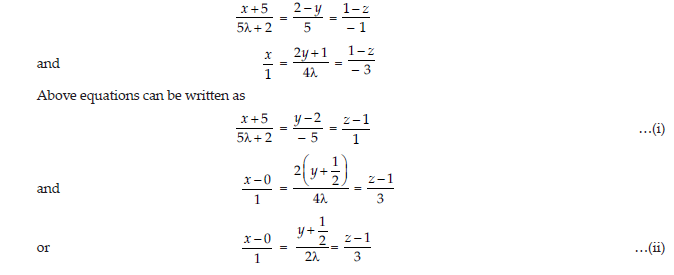
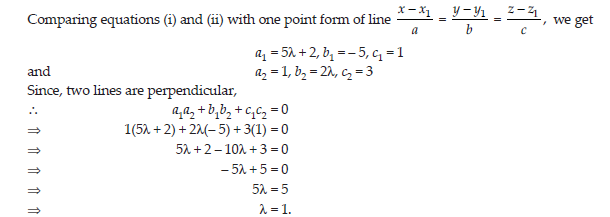
8. Evaluate:∫(3x+ 4)/x2 +12x+ 32
Answer: 

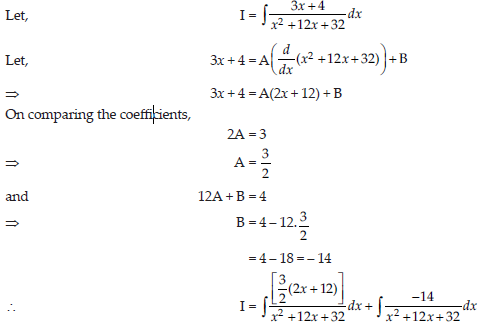
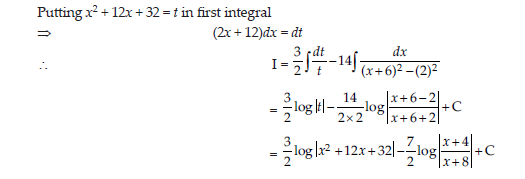
9. 

Answer:

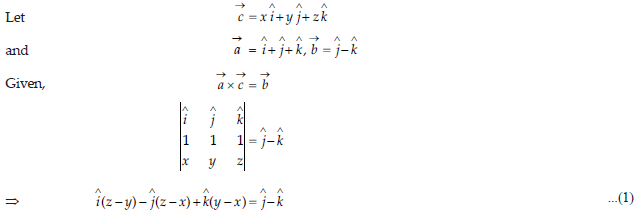
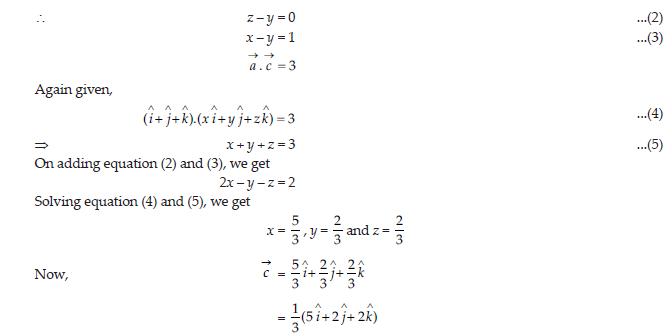
10. Solve the differential equation:
          x dy/dx-y+sin(y/x)=0
OR
Find a particular solution:
                                         dy/dx-ytanx;y=1whenx=0
Answer: The given differential equation is,

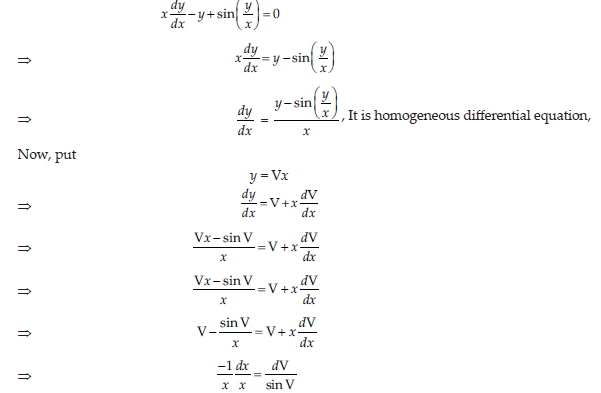
Integrating both sides, we get

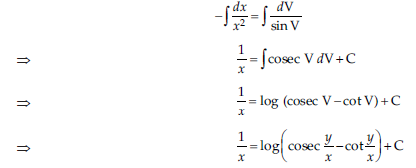
OR

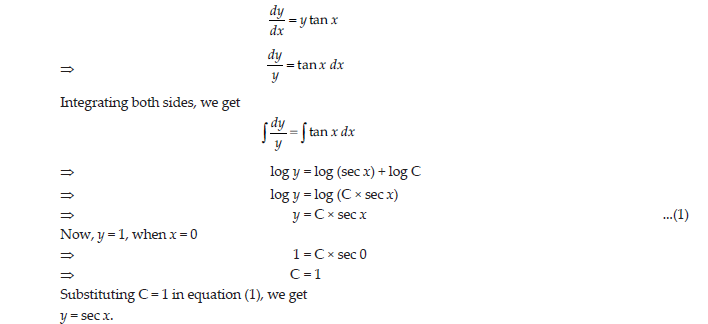
Section – C

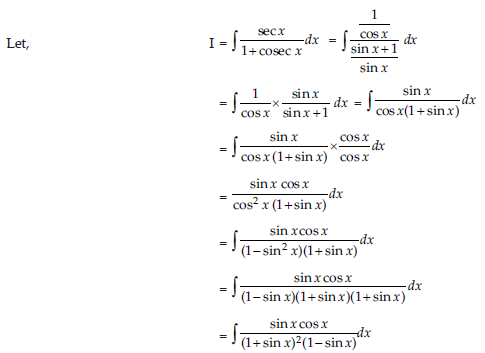
11. Find∫sec/1+cosec x dx
Answer: 

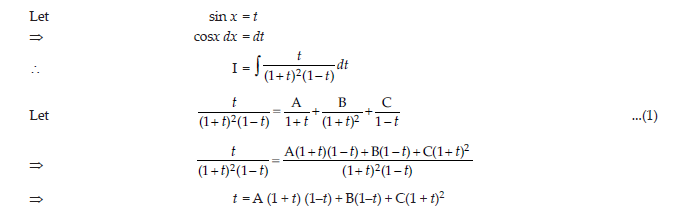
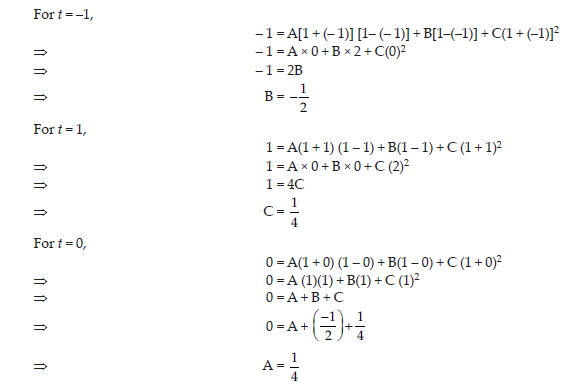
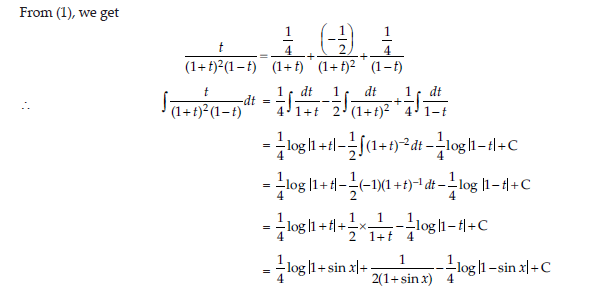
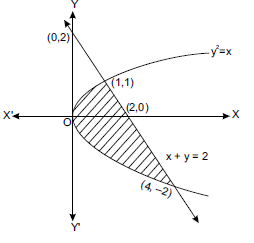
12. Find the area of the region enclosed between the parabola y2 = x and the line x + y = 2.
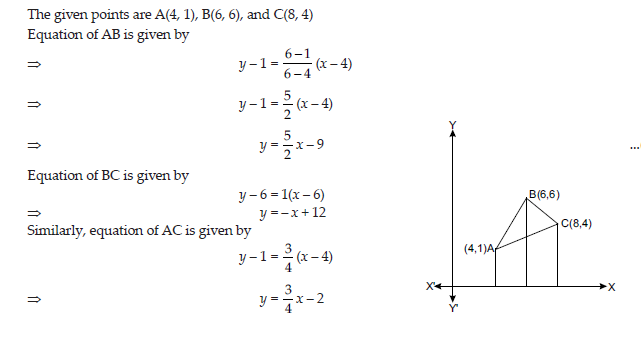
OR
Using integration, find the area of a triangle ABC, coordinates of whose vertices are A(4,1), B(6,6),
C(8, 4).
Answer:  Given, curve is y² = x …(1)
It is a right hand parabola whose vertex is (0, 0)

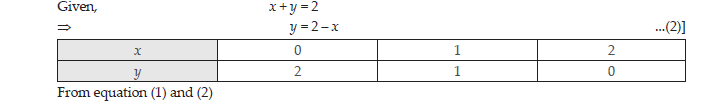
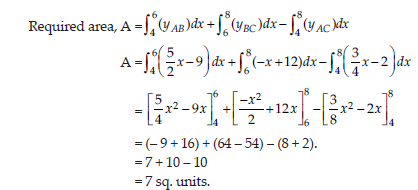
13. Find the equation of the plane passing through the points (1, 0, – 2), (3, – 1, 0) and perpendicular to the plane 2x – y + z = 8. Also find the distance of the plane thus obtained from the origin.
Answer:

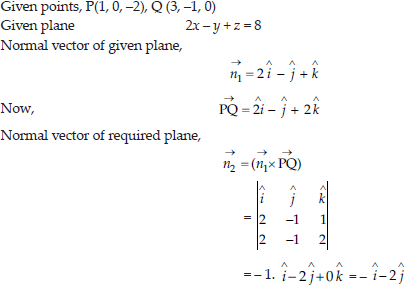
14. Sanjay, Ajay and Vijay are three best friends. After completing their MBA from IIM Lucknow. They apply for the job in the same company for the post of manager in finance department. Chances of selection of Sanjay, Ajay and Vijay are in the same ratio of 1 : 2 : 4. The probabilities that Sanjay can increase the profits of the company by his efforts is 0.8 whereas probabilities for the sam task of Ajay and Vijay are 0.5 and 0.3 respectively.
From the above information attempt the following questions:
(i) A be event of increase the profit then find if it is due to Ajay.
(ii) If E₁, E₂ and E₃, be events of not increase the profits, then find the probability that is due to the appointment of Vijay?
Answer: Let E₁ be event of selecting Sanjay, E₂ be event of selecting Ajay and E₃ be event of selecting Vijay.