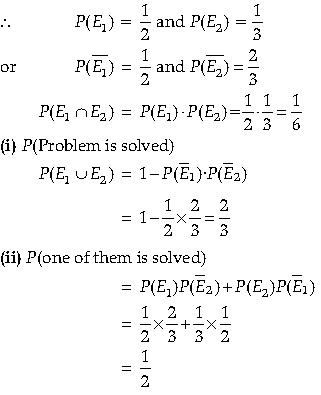Sample Paper Class 12 Mathematics Term 2 Set D
Please refer to Sample Paper Class 12 Mathematics Term 2 Set D with solutions provided below. We have provided CBSE Sample Papers for Class 12 Mathematics as per the latest paper pattern and examination guidelines for Standard 12 Mathematics issued by CBSE for the current academic year. The below provided Sample Guess paper will help you to practice and understand what type of questions can be expected in the Class 12 Mathematics exam.
CBSE Sample Paper Class 12 Mathematics for Term 2 Set D
1. Using integrating by parts in t sin t and integrate it.
OR
Taking x12 as common in denominator and putting

Answer.

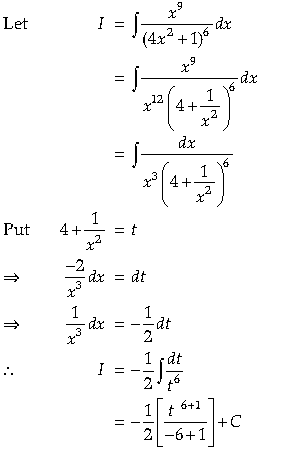

2. Using separate variable and integrate on both sides.
Substituting x = 0, y = π/4 is required equation, we get k = 3√2.
Answer. cos y dx + (1 + 2e–x) sin y dy = 0

3.

Answer.


4. Using formula of distance between two parallel lines

Answer. Distance between two parallel planes,
Ax + By + Cz = d1 and Ax+ By + Cz = d2 is

5. Let E1 : selecting shop X
E2 : selecting shop Y
A : purchased tin is of type B.
Using Baye’s theorem and get P (E2/A)
Answer. E1 : selecting shop X
E2 : selecting shop Y
A : purchased tin is of type B

6. Comparing with dy/dx + Py = Q and obtained the values of P = 1/x and Q = cos x + 1/x sin x Required the solution of differential equation with integrating factor method.
Answer.


7.

Answer.

8. Using partial fraction method in

Substitute these values and integrate it.
Answer.


9. Solve the given equations and find the required points. Now for area, calculate

Answer.
10. Let E1 and E2 be the problem solved by A and B respectively.
Using P(problem is solved) = 1 – P(E̅1).P(E̅2) and P(one of them is solved) = P(E1).P(E̅2)+ P(E2).P(E̅1). Solve it and get answer.
Answer. Let E1 : Problem solved by A
E2 : Problem solved by B