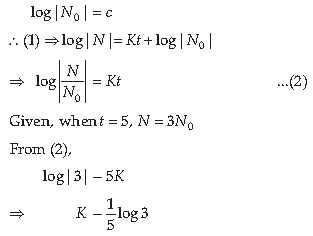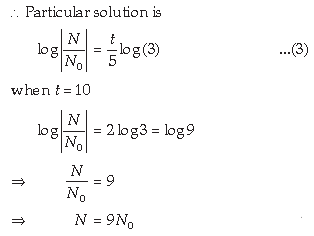Sample Paper Class 12 Mathematics Term 2 Set C
Please refer to Sample Paper Class 12 Mathematics Term 2 Set C with solutions provided below. We have provided CBSE Sample Papers for Class 12 Mathematics as per the latest paper pattern and examination guidelines for Standard 12 Mathematics issued by CBSE for the current academic year. The below provided Sample Guess paper will help you to practice and understand what type of questions can be expected in the Class 12 Mathematics exam.
CBSE Sample Paper Class 12 Mathematics for Term 2 Set C
Section – A

Answer.
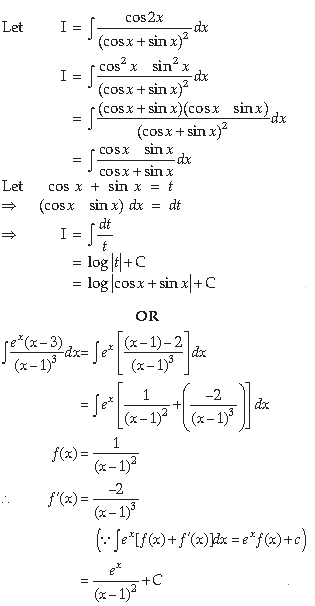
2. Find the sum of the order and the degree of the following differential equations:
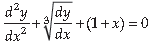
Answer. Here,


3. Find the position vector of a point which divides the join of points with position vectors (a→ – 2b→) and (2a→ + b→) externally in the ratio 2 : 1.
Answer. Equation of line passes to (x1, y1, z1) and (x2 , y2 , z2)
4. Find the equation of line passing through (1, 1, 2) and (2, 3, –1).
Answer. Equation of line passes to (x1, y1, z1) and (x2 , y2 , z2)

5. If A and B are two independent events, then prove that the probability of occurrence of at least one of A and B is given by 1 – P(A’) · P(B’)
Answer. Required probability
= P(A U B)
= P(A) + P(B) – P(A) · P(B)
= P(A) [1 – P(B)] + 1 – P(B’)
= P(A) P(B’) – P(B’) + 1
= [1 – P(B’)] [1 – P(A)]
= 1 – P(A’) P(B’)
6. One bag contains 3 red and 5 black balls. Another bag contains 6 red and 4 black balls. A ball is transferred from first bag to the second bag and then a ball is drawn from the second bag. Find the probability that the ball drawn is red.
Answer. P (Red transferred and red drawn or black transferred and red drawn)

Section – B
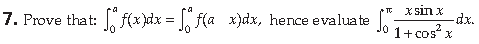
Answer.
8. Find the general solution of the following differential equation: x dy – (y + 2x2)dx = 0
OR
Solve the following differential equation.
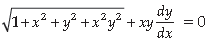
Answer. The given differential equation can be written as



9. Find the area of a rectangle having vertices A, B, C and D with position vectors
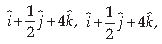
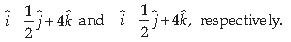
OR
The two vectors ĵ + k̂ and 3 î – ĵ 4 + k̂ represent the two sides AB and AC, respectively of DABC. Find the length of the median through A.
Answer. The position vectors of vertices A, B, C and D of rectangle ABCD are given as:
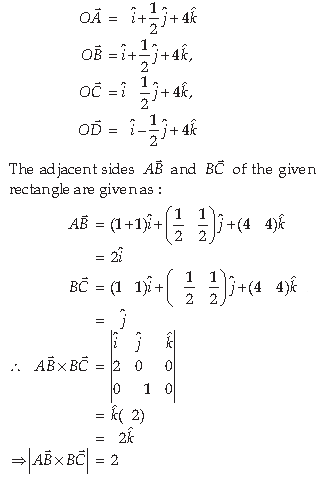
Now, it is known that the area of parallelogram whose adjacent sides are a̅ and b̅ is |a̅ x b̅| Therefore, the area of the given rectangle is |A B̅ x B C̅| =2 sq. units.
OR
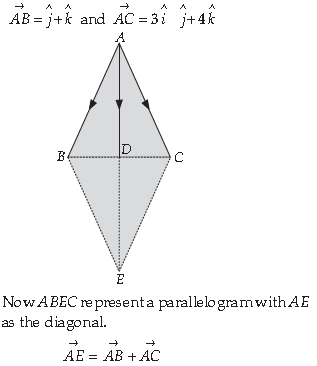

10. Write the sum of intercepts cut off by the plane r̅.(2î + ĵ – k̂) – 5 = 0 on the three axes
Answer. Given, equation of plane is
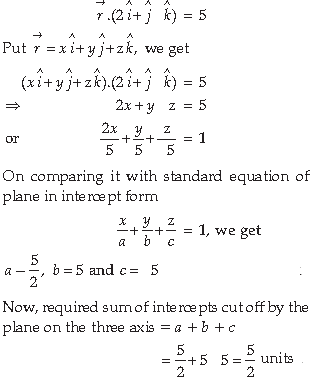
Section – C
11. A bag A contains 4 black and 6 red balls and bag B contains 7 black and 3 red balls. A die is thrown. If 1 or 2 appears on it, then bag A is chosen, otherwise bag B. If two balls are drawn at random (without replacement) from the selected bag, find the probability of one of them being red and another black.
Answer. Let E1 = Selecting bag A
and E2 = Selecting bag B
Probability for selecting bag when die is thrown

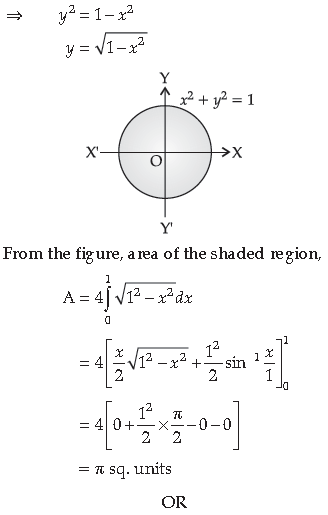
12. Find the area of the region bounded by the circle x2 + y2 = 1.
OR
Find the area of the region bounded the curve y = x + 1 and the lines x = 2 and x = 3.
Answer. We have, x2 + y2 = 1, which is a circle having centre at (0, 0) and radius ‘1’ unit.
Given : Curve y = x + 1 and lines x = 2, x = 3
If x = 2 Þ y = 3
If x = 3 Þ y = 4
So, intersection points (2, 3) and (3, 4)

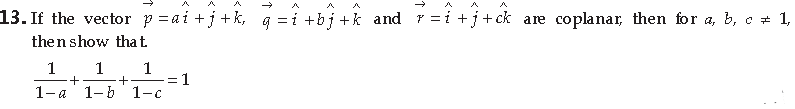
Answer. Since the vector p→ q→ and r→ are coplanar

Case-Based/Data Based
14. The rate of increase in the number of bacteria in a certain bacteria culture is proportional to the number present. Given that the number triples in 5 hours.

Based on the above information, answer the following questions:
(i) If ‘N’ is the number of bacteria, then find the differential equation. Also, find the general solution of
obtained differential equation.
(ii) If N0 is the initial count of bacteria, the find the bacteria count after 10 hours.
Answer. (i) Given that N is the number of bacteria.

(ii) Given, when t = 0, N = N0, from (1)