Please refer to below Exam Question for Class 12 Mathematics Chapter 5 Continuity and Differentiability. These questions and answers have been prepared by expert Class 12 Mathematics teachers based on the latest NCERT Book for Class 12 Mathematics and examination guidelines issued by CBSE, NCERT, and KVS. We have provided Class 12 Mathematics exam questions for all chapters in your textbooks. You will be able to easily learn problems and solutions which are expected to come in the upcoming class tests and exams for standard 10th.

Chapter 5 Continuity and Differentiability Class 12 Mathematics Exam Question

All questions and answers provided below for Exam Question Class 12 Mathematics Chapter 5 Continuity and Differentiability are very important and should be revised daily.

Exam Question Class 12 Mathematics Chapter 5 Continuity and Differentiability

Very Short Answer Type Questions

Question. Find the value of k so that the following function is continuous at x = 2.

Answer. ∵ f(x) is continuous at x = 2

Question. Find the relationship between a and b so that the function ‘f ’ defined by

Answer. ∵ f(x) is continuous at x = 3

Question. Discuss the continuity of the function f(x) at x = 1/2, when f(x) is defined as follows:

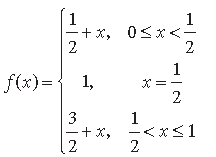
Answer.

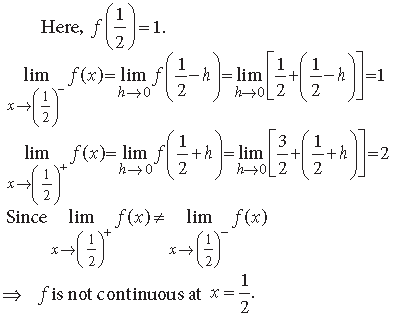
Question.

Answer.

Question. If x = cos t(3 – 2 cos²t) and y = sint (3 – 2 sin²t), find the value of

Answer. Here, x = cos t(3 – 2cos2t), y = sin t(3 – 2 sin2t)

Short Answer Type Questions

Question. Find the values of p and q, for which

Answer. ∴ f(x) is continuous at π/2.

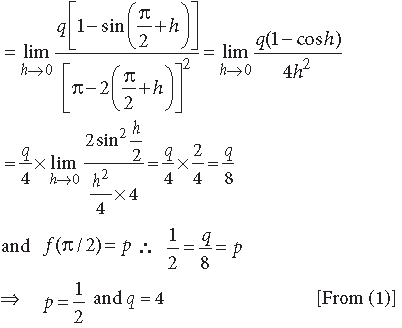
Question. Find the value of the constant k so that the function f, defined below, is continuous at x= 0, where

Answer. ∵ f(x) is continuous at x = 0.
∴ f(0) = k

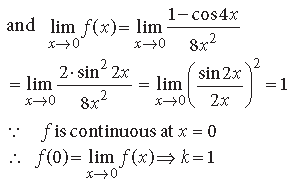
Question. Find the value of k, for which

Answer. ∵ f(x) is continuous at x = 0

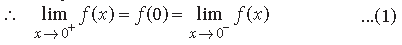
Question.

Answer. ∵ f(x) is continuous at x = 0.

Question.

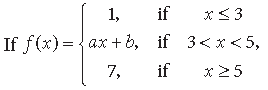
Find the values of a and b so that f(x) is a continuous function.
Answer. Continuity at x = 3
∵ f (x) is continuous at x = 3

Question. For what value of a is the function f defined by

Answer. ∵ f(x) is continuous at x = 0,

Question. Show that the function f(x) defined by

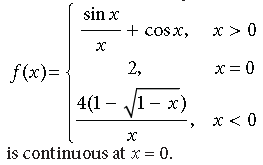
Answer.

Question. If f(x) defined by the following is continuous at x = 0, find the value of a, b and c.

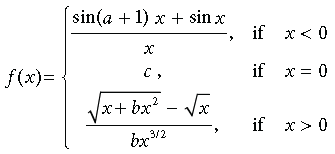
Answer. For f(x) to be continuous at x = 0, we must have

Question. Find the value of k if the function

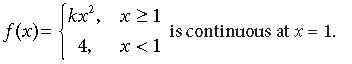
Answer. ∵ f(x) is continuous at x = 1

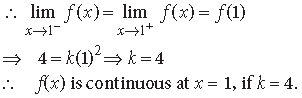
Question.

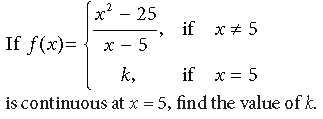
Answer. ∵ f(x) is continuous at x = 5

Question. Find the values of a and b, if the function f

Answer. Given that f(x) is differentiable at x = 1.
Therefore, f(x) is continuous at x = 1

Question.

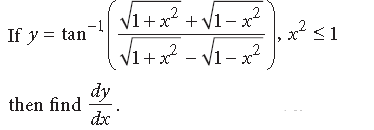
Answer. We have,

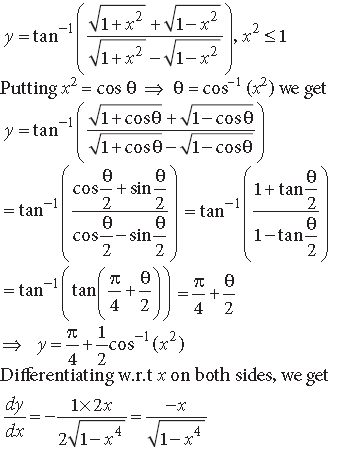
Question.

Answer.

Question. Show that the function f(x) = |x – 1| + |x + 1|, for all x ∈ R, is not differentiable at the points x = –1 and x = 1.
Answer. The given function is f(x) = |x – 1| + |x + 1|

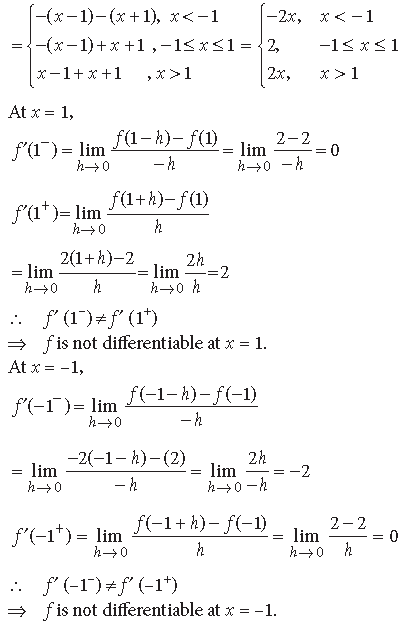
Question. Find whether the following function is differentiable at x = 1 and x = 2 or not.

Answer. At x = 1:

Question. If cosy = xcos(a + y), where cos a ≠ ±1, prove that

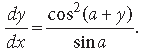
Answer. We have cosy = xcos(a + y)

Question.

Answer.

Question. Show that the function f(x) = |x – 3|, x ∈ R, is continuous but not differentiable at x = 3.
Answer.

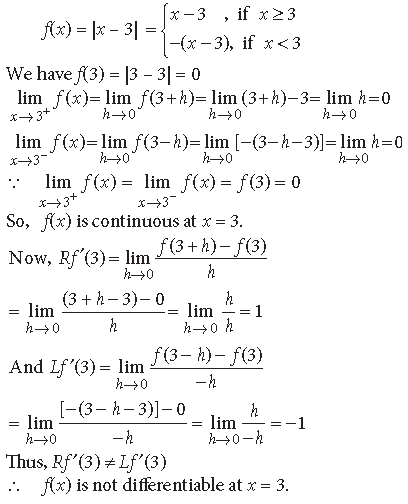
Question.

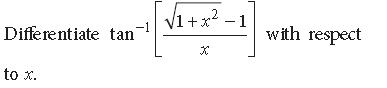
Answer.

Question.

Answer.

Question. If y = a sin x + b cos x, prove that

Answer. Here, y = a sinx + b cos x

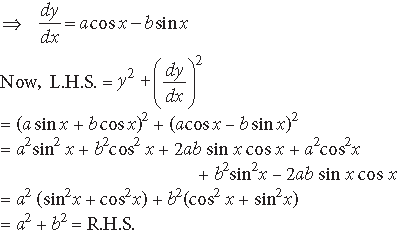
Question. Show that the function defined as follows, is continuous at x = 2, but not differentiable.

Answer.

Question.

Answer.

Question.

Answer. We have, (x² + y²)² = xy
Differentiating w.r.t. x, we get

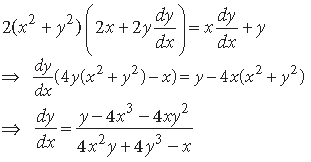
Question.

Answer. We have,

Question.

Answer.

Question. If xy + y² = tan x + y, find dy/dx
Answer. Given, xy + y² = tan x + y
Differentiating w.r.t. x, we get

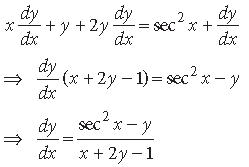
Question.

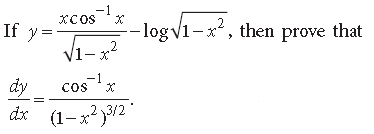
Answer.

Question. If e^x + e^y = e^{x + y}, prove that dy/dx + e ^{y − x} = 0
Answer. Given e^x + e^y = e^x + y ⇒ 1 + e^y–x = e^y …(1)
Differentiating (1) w.r.t. x, we get

Question.

Answer.

Question.

Answer.

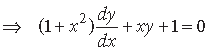
Question.

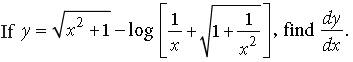
Answer.

Question.

Answer.

Question. Differentiate x^{sin x} + (sin x)^{cos x} with respect to x.
Answer.

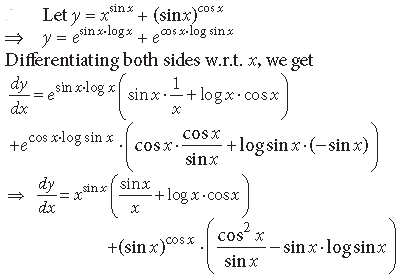
Question. If y = (sinx)^x + sin⁻¹ √x, then find dy/dx
Answer.

Question.

Answer.

Given x^myⁿ = (x + y)^{m + n}
Taking log on both the sides, we get
logx^m + log yⁿ = (m + n)log (x + y)
⇒ m logx + n log y = (m + n) log (x + y)
Differentiating w.r.t. x, we get

Question.

Answer.

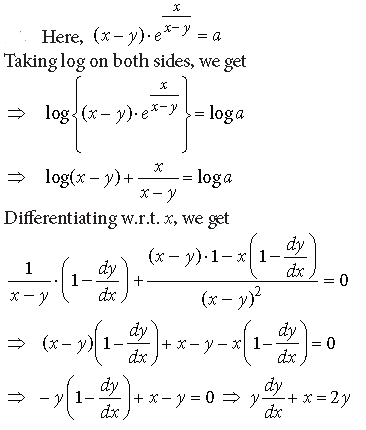
Question. Differentiate the following function with respect to x : (log x)^x + x^logx.
Answer. Let y = (log x)^x + x^{log x}
∴ y = e^{x log (log x)} + e(log x)²
Differentiating w.r.t. x, we get

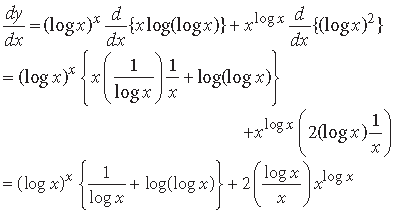
Question.

Answer. Here y^x = e^{y – x}
Taking log on both sides, we get
xlog y = (y – x)log e = y – x
⇒ x(1 + logy) = y

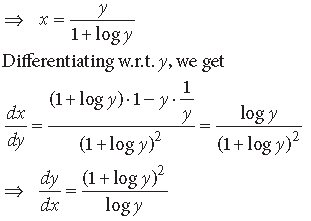
Question. Differentiate the following with respect to x :

Answer.

Question.

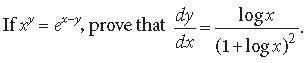
Answer. We have, x^y = e^x–y
Taking log on both sides, we get
y log x =(x – y)log e = x – y

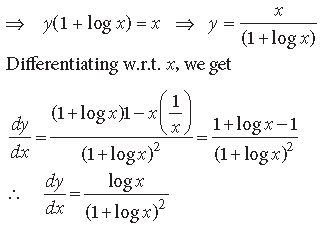
Question. If (cos x)^y = (cos y)^x, find dy/dx.
Answer. We have, (cos x)^y = (cos y)^x
Taking log on both sides, we get
y log (cos x) = x log (cos y)
Differentiating w.r.t. x, we get

Question.

Answer.

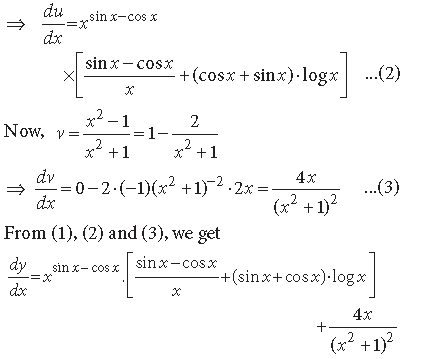
Question. If y = 2cos(log x) + 3sin(log x), prove that

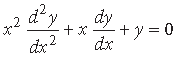
Answer. We have, y = 2 cos (log x) + 3 sin (log x)
Differentiating w.r.t. x, we get

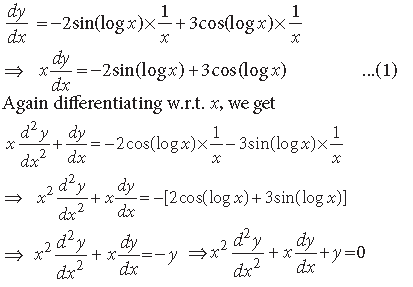
Question. If x = sin t and y = sin pt. Prove that

Answer. We have, x = sin t and y = sin pt

Question.

Answer.

Question. If x = a cos³ θ and y = a sin³ θ, then find the value of

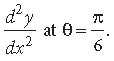
Answer. Here x = a cos³ θy = a sin³ θ

Question.

Answer.

Question. If y = x + tan x, then prove that

Answer. We have, y = x + tan x

Question. Verify Rolle’s theorem for the function f(x) = x² – 4x + 3 on [1, 3].
Answer. We have, f(x) = x²– 4x + 3
(i) f(x) being a polynomial function is continuous in [1,3]
(ii) f(x) being a polynomial function is differentiable in (1, 3)
(iii) f(3) = 3²– 4(3) + 3 = 0 and f(1) = 12 – 4(1) + 3 = 0. Thus f(1) = f(3)
Thus, all the conditions of Rolle’s theorem are satisfied, so there exists atleast one point c ∈(1, 3) such that f'(c) = 0
f ‘(x) = 2x – 4 ⇒ f ‘(c) = 2c – 4
∴ f ‘(c) = 2c – 4 = 0 ⇒ c = 2 ∈(1, 3)
Hence, the Rolle’s theorem is verified.

Long Answer Type Questions

Question. For what value λ of the function defined by

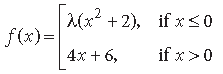
is continuous at x = 0? Hence check the differentiability of f(x) at x = 0.
Answer.

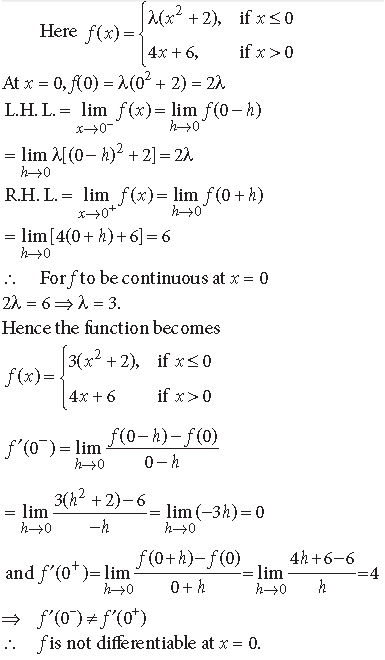
Question. If (tan–1x)^y + y^cotx = 1, then find dy/dx.
Answer. Here, (tan^–1x)^y + y^cotx = 1
⇒ u + v = 1 where u = (tan^–1x)^y and v = y^cotx
Differentiating w.r.t. x, we get