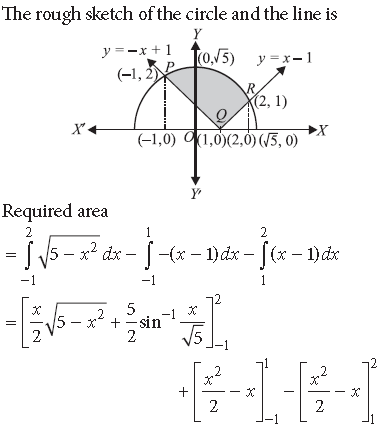
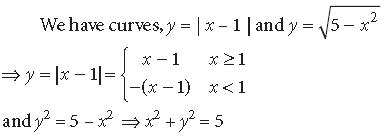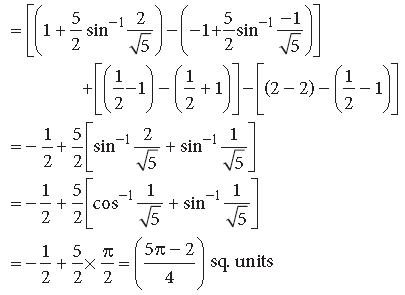Exam Question for Class 12 Mathematics Chapter 8 Application of Integrals
Please refer to below Exam Question for Class 12 Mathematics Chapter 8 Application of Integrals. These questions and answers have been prepared by expert Class 12 Mathematics teachers based on the latest NCERT Book for Class 12 Mathematics and examination guidelines issued by CBSE, NCERT, and KVS. We have provided Class 12 Mathematics exam questions for all chapters in your textbooks. You will be able to easily learn problems and solutions which are expected to come in the upcoming class tests and exams for standard 10th.
Chapter 8 Application of Integrals Class 12 Mathematics Exam Question
All questions and answers provided below for Exam Question Class 12 Mathematics Chapter 8 Application of Integrals are very important and should be revised daily.
Exam Question Class 12 Mathematics Chapter 8 Application of Integrals
Short Answer Type Questions
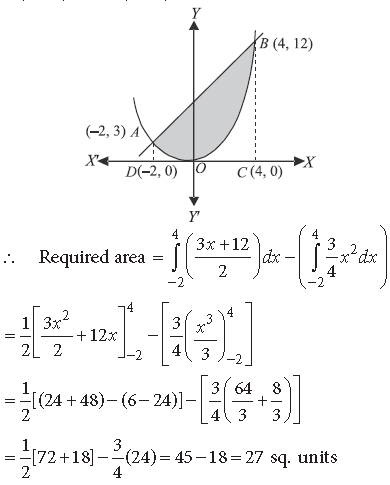
Question. Find the area of the region included between the parabola 4y = 3x2 and the line 3x – 2y + 12 = 0.
Answer.

Question. Using integration, find the area of the region bounded by the curves :
y = |x + 1| + 1, x = – 3, x = 3, y = 0
Answer. Here, y = |x + 1| +1
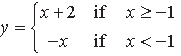
We now draw the lines : y = 0, x = 3, x = –3 and
y = x + 2 if x ≥ -1 ….(i) y = − x if x < – 1 ….(ii)
Lines (i) and (ii) intersect at (– 1, 1)

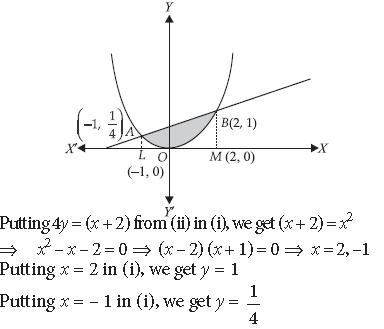
Question. Using integration, find the area bounded by the curve x2 = 4y and the line x = 4y – 2.
Answer. The given curve is x2 = 4y …(i)
The given line is x = 4y – 2 …(ii)

Question. Find the area of the region bounded by the parabola y = x2 and y = |x|.
Answer. The given curves are y = x2 …(i)

Their points of intersection are A (1, 1), O(0, 0) and B (–1, 1).
In view of symmetry, the required area
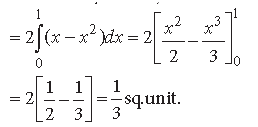
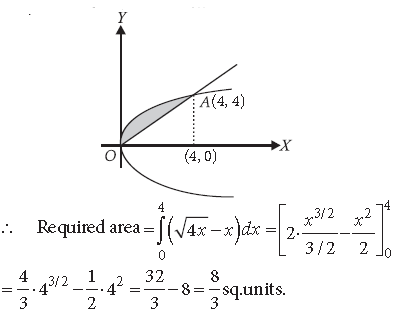
Question. Using integration, find the area of the region enclosed by the curves y2 = 4x and y = x.
Answer. The given curves are y2 = 4x, y = x
They intersect at O(0, 0) and A (4, 4).
Question. Prove that the curves y2 = 4x and x2 = 4y divide the area of the square bounded by x = 0, x = 4, y = 4 and y = 0 into three equal parts.
Answer.
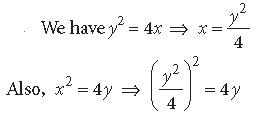
⇒ y4 = 64y ⇒ y = 0 or y = 4
When y = 0, x = 0 and when y = 4, x = 4
So, the points of intersection are O(0, 0) and P(4, 4)
Let A1, A2, A3 be the area denoted in the figure.
We need to prove A1 = A2 = A3.
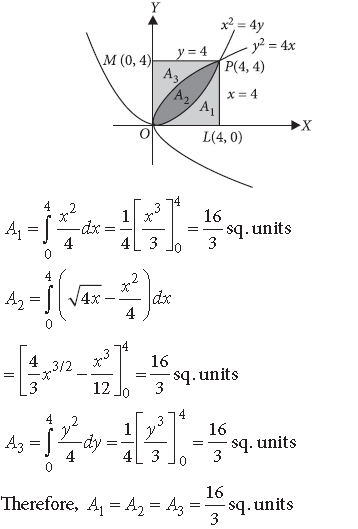
Thus y2 = 4x and x2 = 4y divide the area of square bounded by x = 0, x = 4, y = 4 and y = 0 into three equal parts.
Question. Using integration, find the area of the region bounded by the curves
Answer.
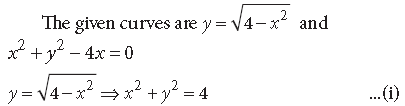
This represents a circle with centre O(0, 0) and radius = 2 units.
x2 + y2 – 4x = 0 ⇒(x – 2)2 + y2 = 4 …(ii)
This represents a circle with centre B(2, 0) and radius = 2 units.
Solving (i) and (ii), we get (x – 2)2 = x2 ⇒ x = 1
∴ y2 = 3 ⇒ y = ± √3

Question. Using integration, find the area of the triangular region whose sides have equations y = 2x + 1, y = 3x + 1 and x = 4.
Answer. The given lines are y = 2x + 1 …(i)
y = 3x + 1 …(ii) and x = 4 …(iii)
Solving (i) and (ii), we get x = 0, y = 1
Solving (ii) and (iii), we get x = 4, y = 13
Solving (iii) and (i), we get x = 4, y = 9
∴ Required area = area (ΔABC)
= area (OABD) – area (OACD)

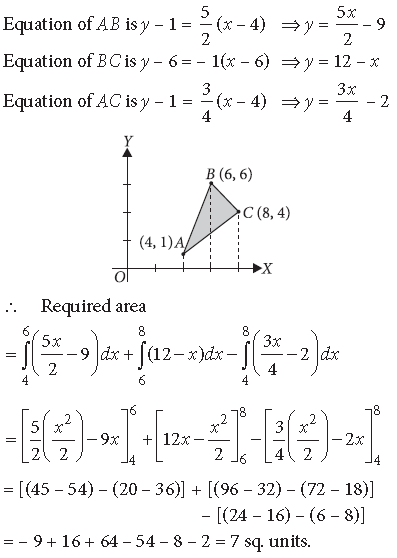
Question. Using integration, find the area of the triangle ABC, coordinates of whose vertices are A(4, 1), B(6, 6) and C(8, 4).
Answer. Here A(4, 1), B(6, 6) and C(8, 4).
Question. Find the area of the circle 4x2 + 4y2 = 9 which is interior to the parabola x2 = 4y.
Answer. The given circle is 4x2 + 4y2 = 9 i.e.
x2 + y2 = 9/4 which has centre (0, 0) and radius 3/2.
The given parabola is x2 = 4y which is symmetrical about positive y-axis with vertex (0, 0).
Solving both the equations, we get

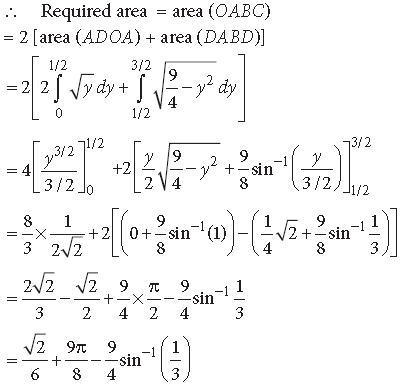
Question. Find the area of the region lying between the parabolas y2 = 4ax and x2 = 4ay, where a > 0.
Answer. The equations of the curves are
y2 = 4ax …(i) and x2 = 4ay …(ii)


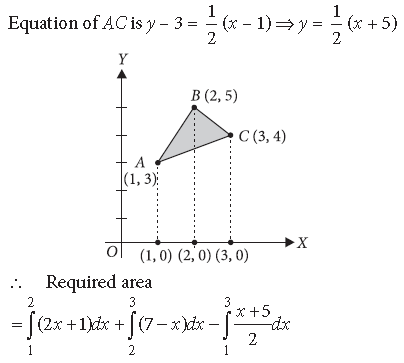
Question. Using integration, find the area of the region bounded by the triangle whose vertices are (1, 3), (2, 5) and (3, 4).
Answer. Let the points be A(1, 3), B(2, 5) and C(3, 4)
Equation of AB is y – 3 = 2 (x – 1) ⇒ y = 2x + 1
Equation of BC is y – 5 = – 1(x – 2) ⇒ y = 7 – x
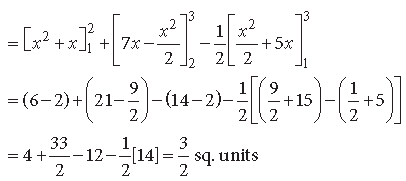
Question. Using integration, find the area lying above x-axis and included between the circle x2 + y2 = 8x and the parabola y2 = 4x.
Answer. We have x2 + y2 = 8x and y2 = 4x
Now, x2 + y2 = 8x ⇒ (x – 4)2 + y2 = (4)2
The centre of circle is (4, 0) and radius is 4.
The point of intersection of circle and parabola are 0(0, 0) and A(4, 4) above x-axis.
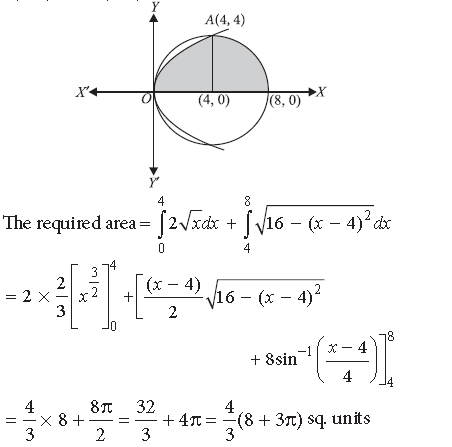
Long Answer Type Questions
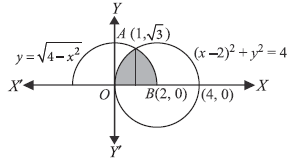
Question. Using integration, find the area of the region enclosed between the two circles x2 +y2 = 4 and (x – 2)2 + y2 = 4.
Answer. The given circles are
C1 : x2 + y2 = 4 …(i) and C2: (x – 2)2 + y2 = 4 …(ii)
Eliminating y from (i) and (ii), we get
4 – x2 = 4 – (x – 2)2 ⇒ 4x = 4 ⇒ x = 1
Putting x = 1 in (i), we get y2 = 3 ⇒ y = ± 3
⇒ Points of intersection of the two circles are A(1, 3) and B(1, − 3)

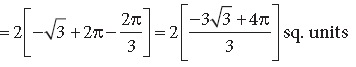
Question. Using integration, find the area of the triangle formed by positive x-axis and tangent and normal to the circle x2 + y2 = 4 at (1, √3) .
Answer. Given equation of circle is x2 + y2 = 4
Differentiate w.r.t. ‘x’ on both sides, we get

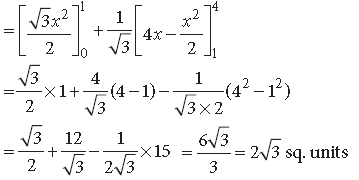
Question. Using integration, find the area of the following region :
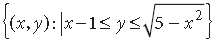
Answer.