Please refer to below Exam Question for Class 12 Mathematics Chapter 13 Probability. These questions and answers have been prepared by expert Class 12 Mathematics teachers based on the latest NCERT Book for Class 12 Mathematics and examination guidelines issued by CBSE, NCERT, and KVS. We have provided Class 12 Mathematics exam questions for all chapters in your textbooks. You will be able to easily learn problems and solutions which are expected to come in the upcoming class tests and exams for standard 10th.

Chapter 13 Probability Class 12 Mathematics Exam Question

All questions and answers provided below for Exam Question Class 12 Mathematics Chapter 13 Probability are very important and should be revised daily.

Exam Question Class 12 Mathematics Chapter 13 Probability

Short Answer Type Questions

Question. A bag A contains 4 black and 6 red balls and bag B contains 7 black and 3 red balls. A die is thrown. If 1 or 2 appears on it, then bag A is chosen, otherwise bag B. If two balls are drawn at random (without replacement) from the selected bag, find the probability of one of them being red and another black.
Answer.

Question. Out of outstanding students of a school, there are 4 boys and 5 girls. A team of 4 students is to be selected for a quiz competition. Find the probability that 2 boys and 2 girls are selected.
Answer. Number of boys = 4
Number of girls = 5
4 students (2 boys and 2 girls) are to be selected.

Question. Assume that each born child is equally likely to be a boy or a girl. If a family has two children, what is the conditional probability that both are girls? Given that
(i) the youngest is a girl.
(ii) atleast one is a girl.
Answer. Let Gi (i = 1, 2) and Bi (i = 1, 2) denote the i^th child is a girl or a boy respectively.
Then sample space is,
S = {G₁G₂, G₁B₂, B₁G₂, B₁B₂}
Let A be the event that both children are girls, B be the event that the youngest child is a girl and C be the event that at least one of the children is a girl.
Then A = {G₁G₂}, B = {G₁G₂, B₁G₂}
and C = {B₁G₂, G₁G₂, G₁B₂}
⇒ A∩B = {G₁G₂} and A∩C = {G₁G₂}
(i) Required probability = P(A/B)

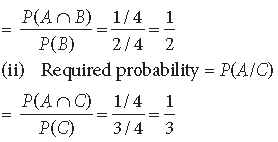
Question. A couple has 2 children. Find the probability that both are boys, if it is known that
(i) one of them is a boy,
(ii) the older child is a boy.
Answer. Let Bi(i = 1, 2) and Gi(i = 1, 2) denote the i^th child is a boy or a girl respectively.
Then sample space is,
S = {B₁B₂, B₁G₂, G₁B₂, G1G₂}
Let A be the event that both are boys, B be the event that one of them is a boy and C be the event that the older child is boy.
A = {B₁B₂}, B = {G₁B₂, B₁G₂, B₁B₂}
C = {B₁B₂, B₁G₂} ⇒ A∩B = {B₁B₂} and A∩C = {B₁B₂}
(i) Required probability = P(A/B)

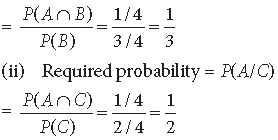
Question. P speaks truth in 70% of the cases and Q in 80% of the cases. In what percent of cases are they likely to agree in stating the same fact? Do you think, when they agree, means both are speaking truth?
Answer. Let E be the event that P speaks truth and F be the event that Q speaks truth. Then, E and F are

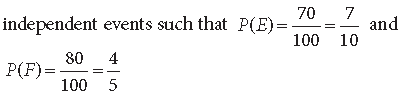
P and Q will agree to each other in stating the same fact in the following mutually exclusive ways:
(I) P speaks truth and Q speaks truth i.e. E ∩ F
(II) P tells a lie and Q tells a lie i.e. E̅ ∩ F̅.
∴ P(P and Q agree to each other)

Hence, in 62% of the cases P and Q are likely to agree in stating the same fact.
P and Q agree means either both P and Q are speaking truth or both are telling lie.

Question. A speaks truth in 75% of the cases, while B in 90% of the cases. In what per cent of cases are they likely to contradict each other in stating the same fact? Do you think that statement of B is true?
Answer. Probability of A speaking the truth is,

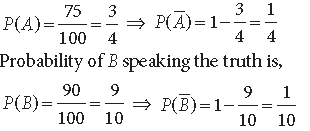
Now A and B will contradict each other in the following mutually exclusive cases:
(i) A speaks the truth and B does not.
(ii) B speaks the truth and A does not.
∴ Probability that A and B will contradict each

i.e., they will contradict each other in 30% of the cases.
We think that statement of B may be false.

Question. The probabilities of two students A and B coming to the school in time are 3/7 and 5/7 respectively. Assuming that the events, ‘A coming in time’ and ‘B coming in time’ are independent, find the probability of only one of them coming to the school in time. Write at least one advantage of coming to school in time.
Answer. Let E be the event that A is coming in time; P(E) = 3 /7
and F be the event that B is coming in time, P(F) = 5/7
Also E and F are given to be independent events.
∴ Probability of only one of them coming to the school in time = P(E) · P(F̅) + P(E̅) · P(F)

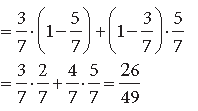
One advantage of coming to school in time is vital to the education process and encourages for a good pattern of work.

Question. A class has 15 students whose ages are 14, 17, 15, 14, 21, 17, 19, 20, 16, 18, 20, 17, 16, 19 and 20 years. One student is selected in such a manner that each has the same chance of being chosen and the age X of the selected student is recorded. What is the probability distribution of the random variable X? Find the mean of X.
Answer. Here the ages of the given 15 students are 14, 17, 15, 14, 21, 17, 19, 20, 16, 18, 20, 17, 16, 19 and 20 years.
∴ The required probability distribution of X is given.

Question. Out of a group of 30 honest people, 20 always speak the truth. Two persons are selected at random from the group. Find the probability distribution of the number of selected persons who speak the truth. Also find the mean of the distribution. What values are described in this question?
Answer. Total number of honest people = 30
The number of people who speak truth = 20
The number of people who do not speak truth = 30 – 20 = 10
Number of selected persons = 2
Let X denote the number of people who speak truth.
∴ X can take values 0, 1, 2

Since, out of 30 honest people, 20 always speak truth. So, the value of truthfulness and morality is described here.

Question. Two cards are drawn simultaneously (without replacement) from a well-shuffled pack of 52 cards. Find the mean and variance of the number of red cards.
Answer. Let X denote the number of red cards. Clearly X can take values 0, 1 or 2.
Here we have 26 red cards in the pack.
∴ P(X = 0) = probability of getting no red card

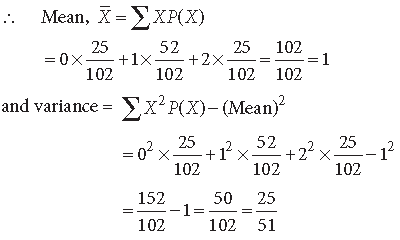
Question. An urn contains 4 white and 6 red balls. Four balls are drawn at random (without replacement) from the urn. Find the probability distribution of the number of white balls.
Answer. Let X denote the number of white balls drawn from the urn. Then X = 0, 1, 2, 3, 4.
Now P(X = 0) = Probability of getting no white ball

Question. Two cards are drawn successively with replacement from a well-shuffled pack of 52 cards. Find the probability distribution of the number of kings and hence find the mean of the distribution. 
Answer. Let X denote the number of kings drawn. Then
X can take the value 0, 1 or 2.
P(X = 0) = Probability of not getting a king in two

Question. A random variable X has the following probability distribution:

Determine:
(i) K (ii) P(X < 3) (iii) P(X > 6) (iv) P(0 < X < 3)
Answer. (i) Since ∑ P(X) = 1
∴ 0 + K + 2K + 2K + 3K + K² + 2K² + 7K² + K = 1
⇒ 10K² + 9K – 1 = 0

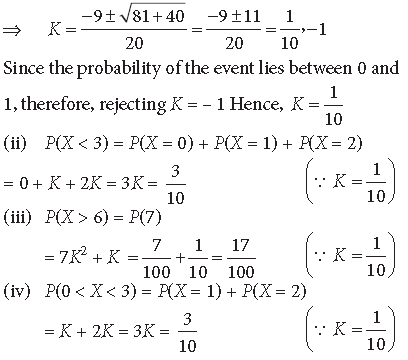
Question. Two cards are drawn simultaneously (without replacement) from a well-shuffled pack of 52 cards. Find the probability distribution of the number of aces. Also find the mean of the distribution.
Answer. Total number of cards = 52
Number of ace cards = 4
Number of other cards = 52 – 4 = 48
Let X be the number of ace cards drawn.
∴ X can take the values 0, 1 or 2
∴ P(X = 0) = P (no ace card)

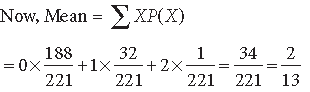
Question. Find mean μ, variance δ² for the following probability distribution :
Answer.

Question. Find the mean μ and variance δ² for the following probability distribution
Answer.

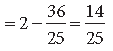
Question. A box has 20 pens of which 2 are defective. Calculate the probability that out of 5 pens drawn one by one with replacement, at most 2 are defective. 
Answer. Let p denote the probability of drawing a defective pen. Then,

Question. An unbiased coin is tossed 4 times. Find the mean and variance of the number of heads obtained.
Answer.  Let p and q be the respective probabilities of occurring a head and tail in single throw of a coin.
Then p = q = 1/2
Let X denote the number of heads obtained when a coin is tossed 4 times.

Question. For 6 trials of an experiment, let X be a binomial variate which satisfies the relation 9P(X = 4) = P(X = 2). Find the probability of success. 
Answer. For a binomial variate X, with n = 6 and probability of success = p, we have

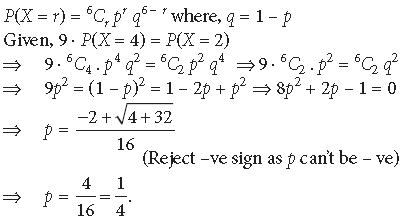
Question. Four cards are drawn successively with replacement from a well shuffled deck of 52 cards, what is the probability that (i) all the four cards are spades? (ii) only 2 cards are spades?
Answer. Let p = Probability of a card to be a spade

Question. An experiment succeeds thrice as often as it fails. Find the probability that in the next five trials, there will be at least 3 successes.
Answer.

Question. How many times must a man toss a fair coin, so that the probability of having atleast one head is more than 80%?
Answer. Suppose a man tosses a fair coin n times, we

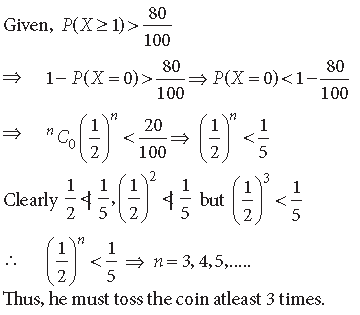
Question. Find the probability of throwing at most 2 sixes in 6 throws of a single die. 
Answer. Here n = 6, p = probability of getting 6 = 1/6

Question. Find the probability distribution of number of doublets in three throws of a pair of dice.
Answer. Total number of outcomes in a throw of a pair of dice = 36.
Doublets appearing in a throw of a pair of dice.
= {(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6)}
∴ Number of doublets = 6
Probability of appearance of a doublet = 6/36 = 1/6
Let X denote the number of doublets in 3 throws of a pair of dice, then

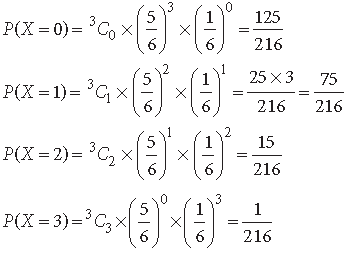
Question. In a multiple choice examination with three possible answers (out of which only one is correct) for each of the five questions, what is the probability that a candidate would get four or more correct answers just by guessing ?
Answer. Let p be the probability of getting correct

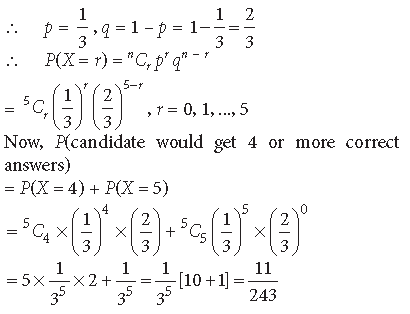
Question. A die is thrown again and again until three sixes are obtained. Find the probability of obtaining the third six in the sixth throw of the dice.
Answer. Probability of obtaining 6 in a throw of die = 1/6
∴ Probability of obtaining a number other than 6 = 5/6
P(Obtaining 3rd six in sixth throw of dice)
= P(Obtaining two sixes in first five throws) × 1/6

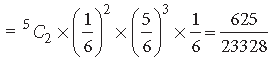
Question. Three cards are drawn successively with replacement from a well shuffled deck of 52 playing cards. If getting a card of spade is considered a success, then find the probability distribution of the number of successes.
Answer. Total number of cards = 52
Number of spade cards = 13

Question. A pair of dice is thrown 4 times. If getting a doublet is considered a success, then find the probability distribution of number of successes.
Answer. Total number of outcomes in a throw of a pair of dice = 36
number of doublets = 6

Question. Find the binomial distribution for which the mean is 4 and variance 3.
Answer. Given, mean = 4 and variance = 3
Then, np = 4 and npq = 3

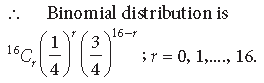
Question. Determine the binomial distribution whose mean is 20 and variance is 16.
Answer. Given, mean = 20 and variance = 16,
Then, np = 20 and npq = 16

Long Answer Type Questions

Question. An urn contains 7 red and 4 blue balls. Two balls are drawn at random with replacement. Find the probability of getting (a) 2 red balls (b) 2 blue balls (c) one red and one blue ball.
Answer. Number of red balls = 7
Number of blue balls = 4
Total number of balls = 7 + 4 = 11
(a) P (2 red balls) = P(RR) = P(R) · P(R)

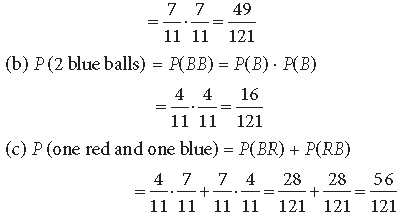
Question. Two groups are competing for the position on the Board of Directors of a corporation. The probabilities that the first and the second groups will win are 0.6 and 0.4 respectively. Further, if the first group wins, the probability of introducing a new product is 0.7 and the corresponding probability is 0.3 if the second group wins. Find the probability that the new product was introduced by the second group.
Answer. Let E₁ and E₂ be the events that the first and second group wins respectively and E be the event of introducing a new product.

Question. A man is known to speak the truth 3 out of 5 times. He throws a dice and reports that it is a number greater than 4. Find the probability that it is actually a number greater than 4.
Answer. Consider the following events,
E₁ : Number is greater than 4
E₂ : Number is not greater than 4
A : The man reports that number greater than 4

Question. In a bulb factory, machines A, B and C manufacture 60%, 30% and 10% bulbs respectively, 1%, 2% and 3% of the bulbs produced respectively by A, B and C are found to be defective. A bulb is picked up at random from the total production and found to be defective. Find the probability that this bulb was produced by the machine A.
Answer. Let E₁, E₂, E₃ and A denote the following events.
E₁ : Bulb manufactured by machine A
E₂ : Bulb manufactured by machine B
E₃ : Bulb manufactured by machine C
A : Bulb is defective

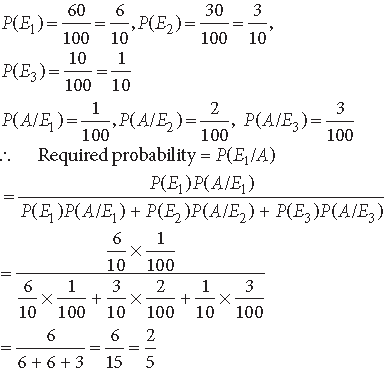
Question. A doctor is to visit a patient. From the past experience, it is known that the probability of the doctor coming by train, bus, scooter or taxi

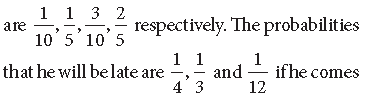
by train, bus or scooter respectively but by taxi he will not be late. When he arrives, he is late. What is the probability that he came by bus?
Answer. Let E₁, E₂, E₃, E₄ be the events that the doctor comes by train, bus, scooter and taxi respectively.

Question. An urn contains 3 white and 6 red balls. Four balls are drawn one by one with replacement from the urn. Find the probability distribution of the number of red balls drawn. Also find mean and variance of the distribution.
Answer. Number of white balls = 3
Number of red balls = 6
Total number of balls = 9
Let X be the random variable denoting the number of red balls drawn.
∴ X can take values 0, 1, 2, 3 or 4
P(X = 0) = Probability of getting no red ball in four draws

Question. Bag A contains 3 red and 5 black balls, while bag B contains 4 red and 4 black balls. Two balls are transferred at random from bag A to bag B and then a ball is drawn from bag B at random. If the ball drawn from bag B is found to be red find the probability that two red balls were transferred from A to B. 
Answer. Let E₁, E₂, E₃ and C be the events as defined below :
E₁ : Two red balls are transferred from bag A to bag B.
E₂ : One red ball and one black ball is transferred from bag A to bag B.
E₃ : Two black balls are transferred from bag A to bag B.
C : Ball drawn from bag B is red.

Question. In a factory which manufactures bolts, machines A, B and C manufacture respectively 30%, 50% and 20% of the bolts. Of their outputs 3, 4 and 1 percent respectively are defective bolts. A bolt is drawn at random from the product and is found to be defective. Find the probability that this is not manufactured by machine B.
Answer. Let E₁, E₂, E₃ and E be the events as follows:
E₁ The bolt is manufactured by the machine A
E2 The bolt is manufactured by the machine B
E3 The bolt is manufactured by the machine C
E The bolt is defective.

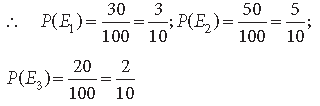
Question. A bag contains 4 red and 4 black balls, another bag contains 2 red and 6 black balls. One of the two bags is selected at random and two balls are drawn at random without replacement from the bag and are found to be both red. Find the probability that the balls are drawn from the first bag.
Answer. Let E₁ and E₂ denote the events of selection of first bag and second bag respectively. Let A be the event that 2 balls drawn are both red.